(2+1)维Burgers方程的新的精确解
2019-12-17李伟
李 伟
(渤海大学 数理学院, 辽宁 锦州 121013)
非线性偏微分方程(组)的解法受到如数学、物理学、工程学和生物学等各学科的广泛重视,为了寻求它们的解法,科学家做了大量而有益的工作,同时得到了一些行之有效的求解方法,如分离变量法、反散射方法、Backlund变换法、Darboux变换法、tanh函数法、Riccati方程法等[1-7]。本文借助行波变换法[8]、拟解法和齐次平衡法[9-11]获得了(2+1)维Burgers方程[12]的新的精确解。
(2+1)维Burgers方程如下:
(ut+αuux+βuxx)x+γuyy=0
(1)
1 (2+1)维Burgers方程的新的精确解
假定式(1)有如下形式的解:
(2)
其中k、h、w是待定常数,ξ0为任意实常数。 将式(2)代入式(1)整理化简得
(kw+h2γ)u″(ξ)+αk2(u(ξ)u′(ξ))′+
βk3u″(ξ)=0
(3)
对式(3)积分2次,积分常数均取0,则式(3)变为
(4)
假定式(4)有如下形式的解:
(5)
M是待定的正整数,ai是待定常数,φ(ξ) 是函数且满足Riccati方程,即
φ′(ξ)=b+φ(ξ)2
(6)
其中,b是任意常数,式(6)有如下形式的解:

(7)
根据齐次平衡法得到方程:M+1=2M,解得M=1。
首先,令拟解(5)的具体形式为
u(ξ)=a0+a1φ(ξ)
(8)
将式(6)和式(8)代入式(4),得到关于φi(ξ),(i=0,1,2)的方程,令φi(ξ),(i=0,1,2)的系数为0,得到关于ai(i=0,1)的代数方程组,利用Mathematica运算,求得如下形式的解:
(9)
将式(7)(8)和(9)代入式(2),得到式(1)的新的精确解,即
(10)

其次,令拟解(5)的具体形式为:
u(ξ)=a0+a1φ(ξ)+a2φ-1(ξ)
(11)
将式(6)和式(11)代入式(4),得到关于φi(ξ)(i=0,±1,±2)的方程,令φi(ξ)(i=0,±1,±2)的系数为0,得到关于ai(i=0,1,2)的代数方程组,利用Mathematica运算,求得如下形式的解:
(12)
将式(7)(11) 和(12)代入式(2),又得到式(1)的新的精确解,即
(13)
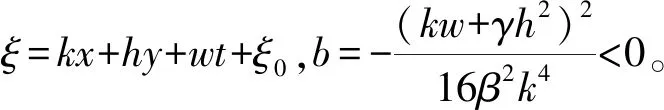
在这2种拟解中都需要φ(ξ)满足Riccati方程。下面用更直接的方法获得更广泛的精确解,令方程(4)拟解的形式为:

借助齐次平衡法,仍解得M=1,因此
(14)
将式(14)代入式(4),同时由于tanh2ξ=1-sech2ξ,得到关于tanhξ,sechξ的方程且tanhξ的次数为0或1,之后令tanhiξsechjξ(i=0,1;j=0,1,2,…)的系数为0,得到关于ai(i=0,1)的代数方程组,利用Mathematica运算,求得如下形式的解:
(15)
将式(15)代入式(14)就得到式(1)的新的精确解,即:

2 结束语
利用行波变换法、拟解法、齐次平衡法获得了Burgers的全新的精确解。这种方法也可用于解其他非线性偏微分方程(组)。精确解的获得将为近似计算、定理分析等现实问题提供必备的基础。
