气力推进艇螺旋桨静态推力计算及检测试验
2019-12-17袁善坤储江伟李洪亮詹长书张民安
袁善坤,储江伟,李洪亮,詹长书,张民安
(东北林业大学 交通学院, 哈尔滨 150040)
气力推进艇是由发动机驱动后置螺旋桨旋转产生向后的推力,使其依靠空气动力在水中行驶[1],主要应用于水面、雪地、冰面、沼泽等一般船舶无法行驶的特殊地段,供人们进行旅游观光、生态勘察、救灾救援以及运输作业等[2-3]。国外对于气力推进艇的研究开展较早,形成了较完整的理论设计、工业制造及实际应用体系。
气力推进艇螺旋桨的静态推力是在气力推进艇不动的条件下,测试的螺旋桨产生的推力[3]。螺旋桨静态推力是气力推进艇动力系统匹配和螺旋桨应用选型的主要技术参数,对螺旋桨的实际应用具有指导意义。通过编程计算和试验检测气力推进艇螺旋桨的静态推力,可为进一步优化螺旋桨的翼型设计和提高使用性能提供参考[4]。
1 螺旋桨推力计算方法
1.1 基于叶元体理论的推力计算
将螺旋桨叶片沿径向细分为多个离散的截面称为叶元体,如图1所示。对于每个叶元体只分析其轴向速度和角速度分量,忽略其他截面的诱导流,且对每部分进行独立地分析,求出任意半径r上的叶元体的作用力。
在图1中的AA截面处,取dr段的叶元体进行分析。令几何螺旋角为θ,攻角为αk。当流体以速度V1流向此叶元体时,流体轴向速度矢量V0和流体角速度矢量V2,并产生了升力L和阻力D,如图2所示。图2中,Q为驱动转矩,T为推力[4]。
推力和升力方向之间的角度差定义为φ:
φ=θ-αk
(1)
将升力dL分解为沿螺旋桨轴向的分力dLα和旋转方向的分力dLt,;将升力dD分解为沿螺旋桨轴向的分力dDα和旋转方向的分力dDt。 叶元体的推力dT和转矩dQ可以表达为[5]:
dT=dLa-dDa=dL·cosφ-dD·sinφ
(2)
(3)
叶元体产生力区域面积是c·dr,c为叶片弦长,则叶元体所受的升力与阻力表达式为[6]:
(4)
(5)
式中:CL为升力系数;CD为阻力系数;ρ为空气密度,1.225 kg/m3。
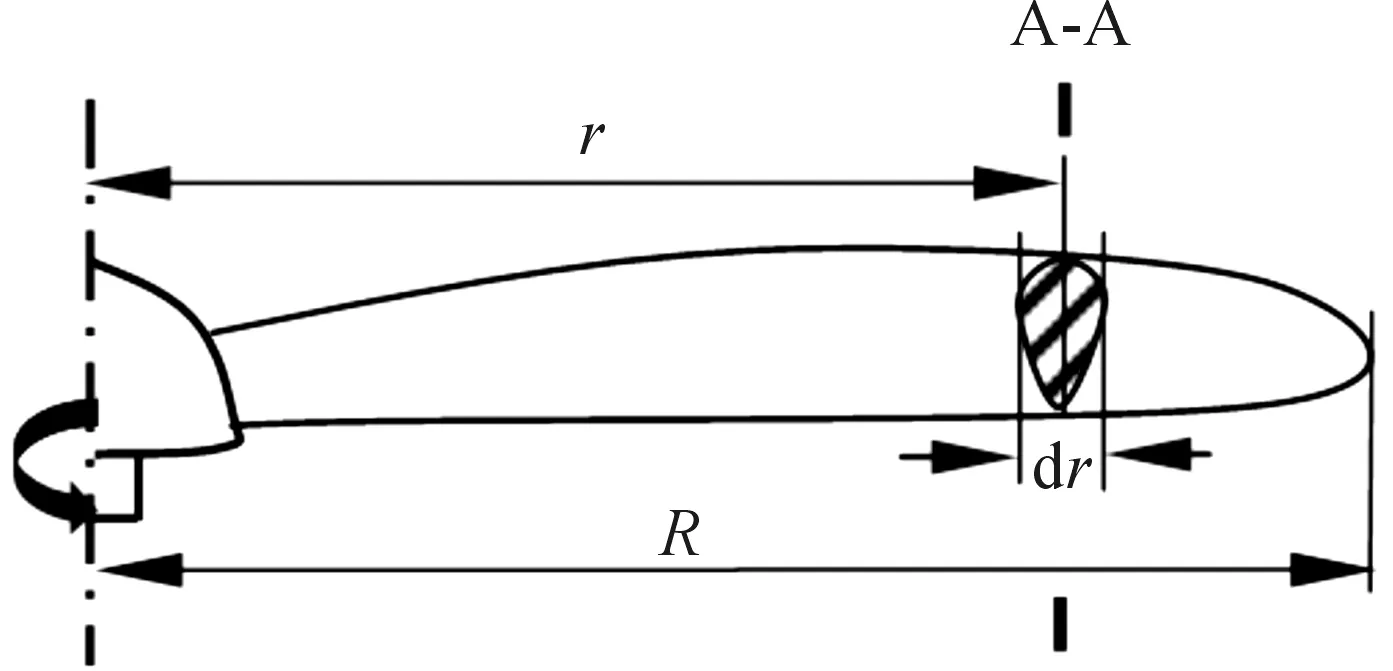
图1 叶元体截取位置
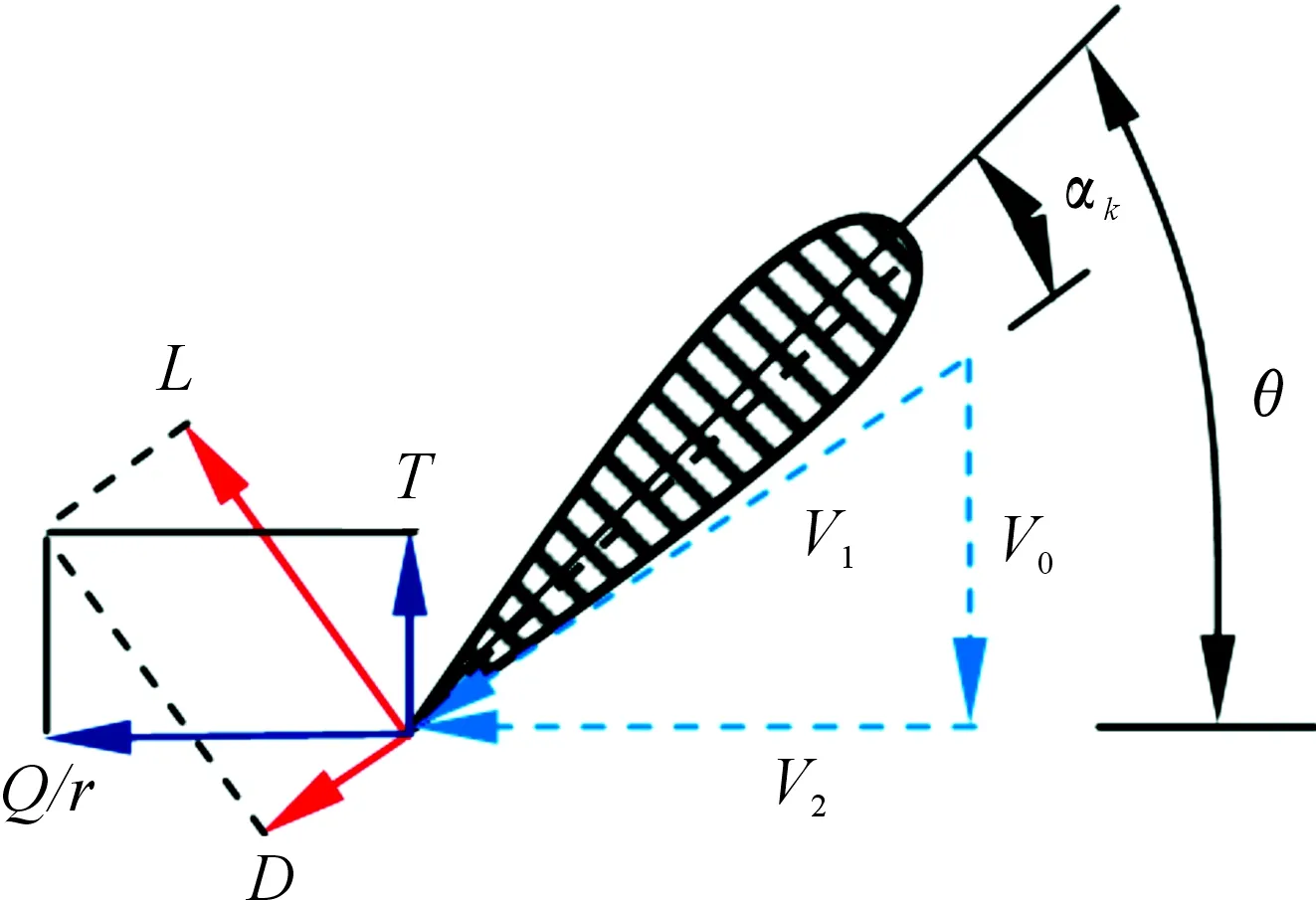
图2 叶元体截面速度与作用力分析
当螺旋桨叶片的数量为B时,则
(6)
(7)
根据图2所示,流体的合速度V1和攻角αk可以表达为:
(8)
αk=θ-tan-1(V0/V2)
(9)
式中:V0等于气力推进艇的前进速度Vinf,V2等于叶元体旋转的线速度ωr。
引入轴向诱导因子a和周向诱导因子b,则V0和V2可以表达为[7]
V0=Vinf+a·Vinf
(10)
V2=ωr-b·ωr
(11)
1.2 基于动量守恒理论的推力计算
假设螺旋桨在无限的静止流体中以速度Vinf前进,应用运动转换原理,即认为螺旋桨是固定的且被包在空气流管里,空气自无穷远前方以速度Vinf流向螺旋桨。
根据动量守恒定理,作用在流体上的力等于单位时间内流体的动量的变化量[8-9],则在叶元体上产生推力的表达式为:
dT=ΔP=dm·ΔV=ρ2πrdrV0(Vslip-Vinf)
(12)
式中: ΔP为动量的变化量;dm为叶元体质量;ΔV为速度的变化量;Vslip为滑流速度(m/s)。
由伯努利方程和动量守恒,可知螺旋桨盘面的轴向速度V0是空气自由流速Vinf和气流速度的平均值Vslip[10]:
V0=(Vinf+Vslip)/2
(13)
则
Vslip=Vinf(1+2a)
(14)
因此,由动量守恒理论得到的螺旋桨推力为:
(15)
根据角动量守恒,考虑其与轴向速度的变化相结合可以证明滑流角速度是螺旋桨盘r处值的2倍,即
Vθ=2bωr
(16)
即
(17)
螺旋桨总体推力T及所需的驱动转矩Q等于其径向叶元体推力dT和转矩dQ的总和,即
T=∑dT
(18)
Q=∑dQ
(19)
2 螺旋桨推力及推力系数计算
2.1 迭代计算法及编程
上述式(6)~(9)(15)和(17)中是含有4个未知变量的dT、 dQ、a和b的方程,可以利用迭代的方法求出未知数。采用Matlab编写计算程序的流程,如图3所示。计算过程如下:

图3 计算流程
1) 假设诱导因子a和b值并赋予初始值,利用式(8)和式(9)计算出流体的合速度V1和攻角αk;
2) 根据叶元体原理得出的式(6)和(7),估计叶元体推力和转矩;
3) 根据得出的推力与转矩的近似值,利用动量守恒定理得出的式(15)和(17),修正诱导因子a和b;
4) 重复1)至3)计算过程,使a和b的值在指定的收敛范围内;
5) 赋予诱导因子a和b的收敛值,利用式(8)和(9)计算得到叶元体推力和转矩的预测计算值。
2.2 相关计算参数
以某型号气力推进艇螺旋桨叶片为研究对象,如图4所示。螺旋桨叶片半径为90 cm,其各半径位置的弦长c和厚度h的数值如表1所示。
在计算中假定螺旋桨截面为相对简单的标准线性化翼型设计及叶片具有恒定的螺距p。螺距p由标准螺距方程计算得到。
升力系数和阻力系数与桨叶的材料、形状等因素有关,精确计算比较复杂,根据该螺旋桨的基本叶形,由Fluent软件计算得到叶形在不同雷诺数和不同迎角下相对应的升力系数和阻力系数。经拟合数据得,升力系数CL和攻角αk略成线性关系,模型可取比例系数为6.2。
CL=6.2αk
(20)
阻力系数与升力系数的函数关系为:
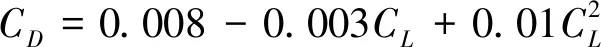
(21)
P=2πrtanθ
(22)

图4 桨叶实物

位置弦长c/mm厚度h/mmR8090.9R130140.8R163170.7R190230.6R213270.5R230330.4R234360.3R232350.2R210350.1R8034
2.3 螺旋桨推力计算结果
在气力推进艇螺旋桨为2桨叶或3桨叶时,计算得到不同螺距角时的推力,如图5所示。
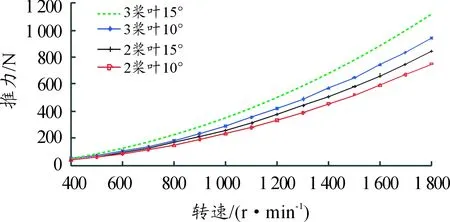
图5 螺旋桨推力计算结果
3 螺旋桨推力测试试验及结果分析
3.1 静态推力测试方法
由气力推进艇样机、电子拉力计、联接钢丝绳、滚杠及固定桩等构成静态推力测试系统,如图6所示。气力推进艇样机选用4G63S4T增压汽油发动机。发动机的最大功率是130 kW/5 000 r/min,最大转矩是253 N·m/2 500 r/min。测试时将滚杠放置在平整、光滑的水磨石地面上,并将气力推进艇安放在滚杠上,以尽可能地减小摩擦阻力。
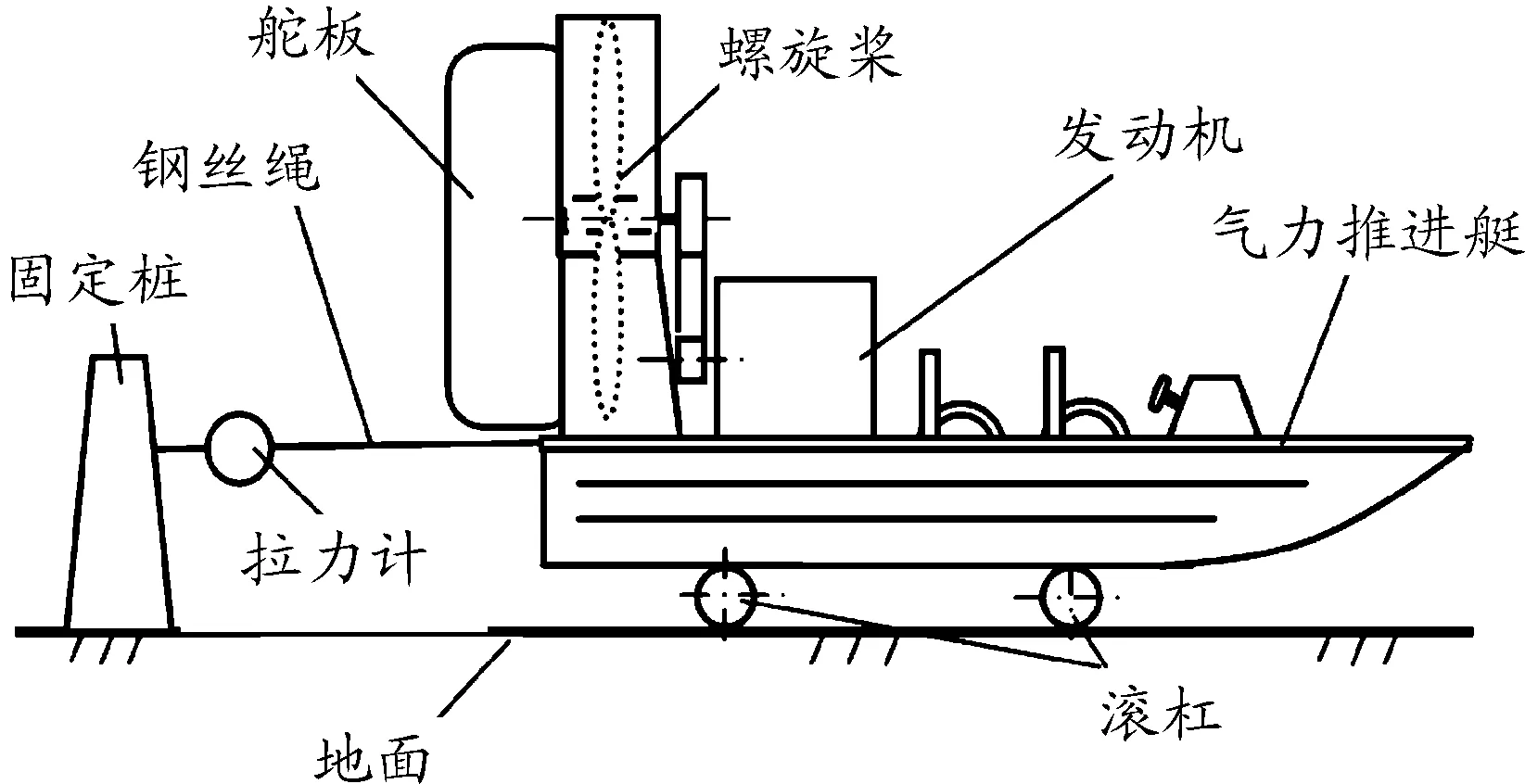
图6 静态推力测试系统
3.2 静态推力测试结果
在螺距角不同时,3桨叶螺旋桨静态推力测试结果,如表2、表3所示。
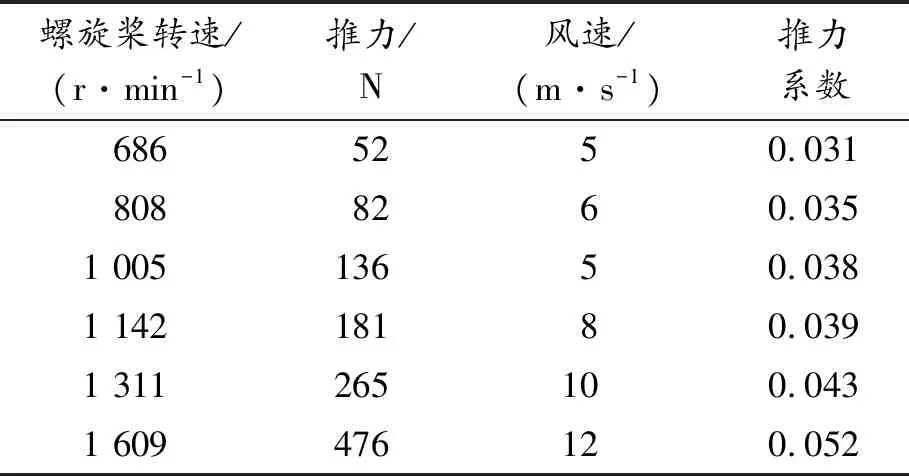
表2 螺距角10°时3桨叶静态推力测试结果

表3 螺距角15°时3桨叶静态推力测试结果
在螺距角不同时,2桨叶螺旋桨静态推力测试结果,如表4、表5所示。
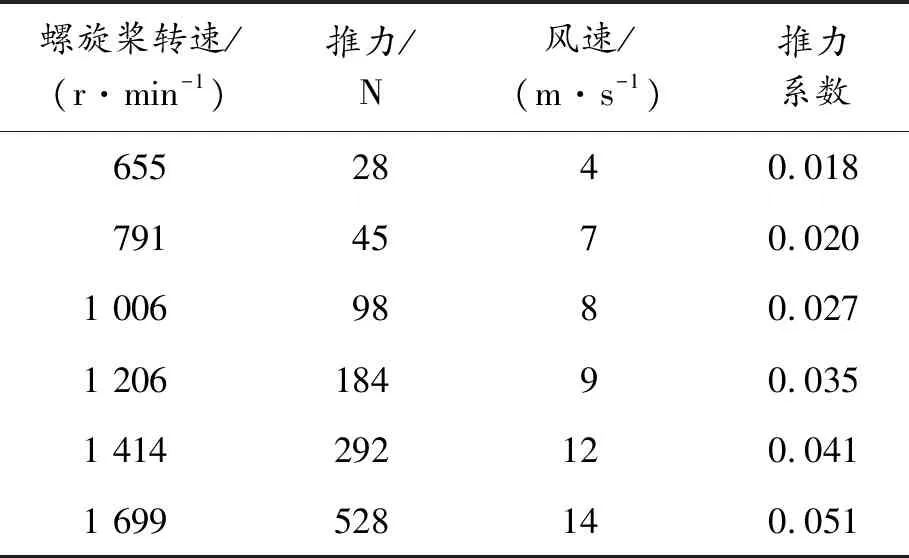
表4 螺距角10°时2桨叶静态推力测试结果
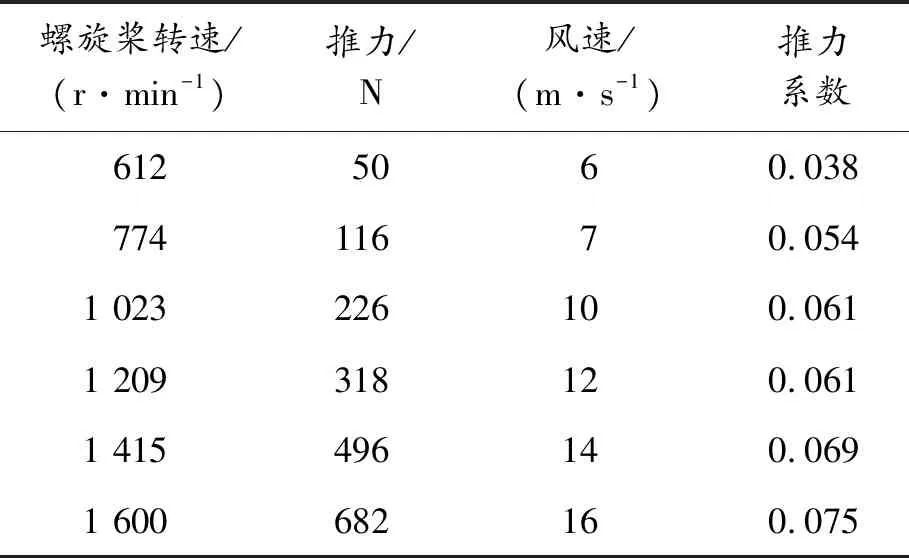
表5 螺距角15°时2桨叶静态推力测试结果
3.3 螺距角不同时推力计算结果与检测数据对比
螺距角不同时,3桨叶螺旋桨推力计算结果与测试数据的对比如图7所示。可以看出,推力计算结果与测试数据都随螺旋桨转速的变化呈抛物线形。
相同螺旋桨转速下,推力计算结果与测试数据的平均误差见表6。螺距角相同时,3桨叶的推力计算结果与测试数据的平均误差小于2桨叶;螺距角为15°时的推力计算结果与测试数据的平均误差大于螺距角为10°时的误差。
推力计算结果大于试验检测数据的原因主要是:在计算中采用的叶元体理论和动量守恒理论主要研究对象是理想螺旋桨,即假设空气可以自由通过螺旋桨盘面,空气速度和压力在螺旋桨盘面上均匀分布,空气为不可压缩的理想流体以及螺旋桨截面为相对简单的标准线性化翼型的影响。

图7 螺距角不同时推力计算与测试

螺旋桨结构螺距角θ绝对误差N相对误差/%2桨叶10°509.615°8211.62桨叶10°-227.515°7713.8
3.4 桨叶数不同时推力计算结果与检测数据对比
螺旋桨的桨叶数增多时,单位时间内流过螺旋桨盘面的流体质量增加,所以空气单位时间内获得的动量增加,即桨叶数多时推力也增加。在相同转速下,3桨叶产生推力的计算结果比2桨叶的推力大,如图8所示。但是,检测获得的不同桨叶数推力的增加幅度小于计算结果的增加幅度。但是,检测获得的不同桨叶数推力的增加幅度小于计算结果的增加幅度。这是因为螺旋桨数目增多后,桨叶之间的相互扰动变大,前一个螺旋桨桨叶的绕流会影响下一个螺旋桨桨叶周围的流场分布,所以检测获得的不同桨叶数推力的增加幅度减小。

图8 桨叶数不同时推力计算与测试结果
4 结论
1) 在螺距角和桨叶数不同时,螺旋桨推力计算结果与测试数据随螺旋桨转速的变化都呈抛物线形,即推力的计算结果与测试数据的变化规律相同,因此计算结果具有参考意义。
2) 在螺旋桨转速、螺距角和桨叶数不同时,其平均绝对误差有差异,最大平均误差为87 N,相对误差为10%~20%。
3) 螺旋桨推力计算结果与测试数据有差异的主要原因是计算公式的假设条件理想化及检测试验中存在着摩擦阻力等因素的影响。
