波形钢腹板的弹性局部剪切屈曲强度

王银辉，郑 亮，管炎增，王 韬

(1. 重庆交通大学 土木工程学院，重庆 400074； 2. 浙江大学宁波理工学院 土木建筑工程学院，浙江 宁波 315100； 3. 中国铁路上海局集团有限公司，上海 200071)

0 引 言

波形钢腹板(以下简称波板)的平面外刚度远大于一般的平钢腹板(以下简称平板)，因而波板的平面外稳定性较平板强许多。大型构件中常用波板代替加劲肋的平板，防止屈曲失稳。作为梁腹板的波板，由于手风琴效应，基本上只受剪力不受弯矩[1-2]，理论研究只需考虑波板受纯剪力。波板的弹性剪切屈曲有局部屈曲、整体屈曲和合成屈曲3种形式，其中局部屈曲是较为常见的屈曲形态。

基于平板弹性屈曲理论[3-4]，可得出波板的弹性局部屈曲强度建议计算式。目前为止，大多数国内外研究仍然沿用此法[5-13]，但建议公式并不能精确计算弹性局部屈曲强度，应用范围有一定的局限性。E. Y. SAYED-AHMED[7]指出：平子板和斜子板等宽时,可使波板抗剪强度趋近于剪切屈服应力的范围更广,因此提出了采用平子板和斜子板等宽的建议，使得弹性局部屈曲强度计算法得以简化。但该建议并不能代表最优方案，在R. SAUSE等[11]统计的实验数据中不难发现, 有些情况下平子板和斜子板不等宽的波板抗屈曲效果更好。另外，采用嵌入型连接方式的波板的平子板需要焊接于混凝土内的钢棒上。为了保证足够的焊缝长度，可能需采用相对较宽的平子板，如将两子板限制为等宽，则不利于波板的尺寸设计。目前的弹性局部屈曲强度计算公式局限于两子板宽度相近的波板，而两子板宽度差距较大的波板弹性局部屈曲强度没有明确的计算公式。

另一方面，由于合成屈曲的研究是在局部屈曲和整体屈曲研究的基础上展开的，局部屈曲强度建议公式的局限性导致合成屈曲强度建议计算公式的应用范围也受到限制。例如，朱力等[9-10]、R. SAUSE等[11]、M. LEBLOUBA等[12]在合成屈曲的研究基础上，结合了大量试验结果提出了极限剪切强度建议计算式，但都只能适用于平子板和斜子板宽度相近且波角为22°以上的波板，其中一个重要原因在于弹性局部屈曲强度建议计算公式的应用范围受到限制。

综上，现有的屈曲强度建议计算式存在局限性，不能满足波板形状多样化设计和优化设计的需要，屈曲强度的计算方法有待改进和提升。相较于整体屈曲，局部屈曲后的腹板能更好发挥屈曲后强度，桥梁工程中的箱梁波板宜设计为局部屈曲破坏模式以避免整体屈曲。例如，朱力等[9]分析认为重庆市大堰河桥的波板屈曲破坏模式接近于局部屈曲破坏模式，这对保证结构的承载力和延性十分有利；同时，实验研究表明[10]：波板接近于局部剪切屈曲的合成剪切屈曲破坏模式较整体剪切屈曲破坏模式在屈曲后保持着更高的承载能力。李立峰等[13]的研究认为，波形较疏，倾向局部屈曲波板的材料利用率更高，且局部屈曲强度建议小于0.5倍的整体屈曲强度，以确保屈曲破坏模式为局部屈曲。

鉴于以上，出于实用性的考虑，笔者将重点讨论波板弹性局部屈曲强度计算式的修正方法。试图以传统的矩形平板屈曲研究成果为基础[1-2]，结合大量的有限元数值模拟和参数分析法，对各个参数进行分析，从而确定影响屈曲强度的重要参数，提出适用范围较广精度较高的弹性局部屈曲强度建议计算式。

1 有限元模型建立

在实际波板箱梁中，波板受上下混凝土顶板、底板和加劲肋的约束，受力较为复杂，难以研究。从较保守的工程设计角度出发，应用有限元法(FEM)建模时不考虑混凝土顶底板和加劲肋对波板边界的转动约束作用，采用四边简支的边界。应用通用有限元程序ABAQUS对波板弹性屈曲进行分析。分析对象的截面几何参数如图1，波数取m=6，w=max(b,c)为较宽子板宽度，w2=min(b,c)为较窄子板宽度，两者的比值w2/w定义为窄宽比。有限元模型如图2，约束AC边的自由度x，y，z；约束BD边的自由度x，y；约束AB和CD边的自由度x，y。此时模型的边界条件为四边简支。沿BD边施加剪力F。此时模型的边界条件和加载方式可保证波腹板的受力状态为纯剪状态。模型中单元均采用四边形壳单元(S4R)，设置钢材的弹性模量E=205 000 MPa，泊松比υ=0.3。取一阶特征值Fcr及所对应的屈曲模态作为有限元计算分析结果，弹性剪切屈曲强度为n,el=Fcr/(ht)，h和t为波板的高度和厚度。

笔者重点研究局部屈曲，采用厚度极小的波板，并且建模时进行了细密的网格划分。

图1 波板的几何参数Fig. 1 Geometric parameters of trapezoidal corrugated steel webs

图2 有限元模型示意Fig. 2 Finite element model

2 弹性局部屈曲强度计算式适用性分析

首先将有限元法得出的各种形状波板的弹性局部屈曲强度与现有的弹性局部屈曲强度计算公式的计算结果进行比较，对现有公式的适用情况进行分析。

由于波板中的子板(包括平子板和斜子板)可以认为是长条形的矩形平板，现有的波板屈曲强度计算公式实质上直接采用了四边简支矩形平板的屈曲强度计算公式[2]，表示如式(1)：

(1)

式中：w=max(b,c)为较宽子板宽度;υ为泊松比。

波板的局部屈曲发生在各个子板。从波板中抽离出1块子板，此时抽离出来的子板模型虽可视为平板模型，但子板的屈曲强度由长边的约束情况所主导。子板的边界情况并不一定为简支，应视具体情况而定。直接使用式(1)计算波板的弹性局部屈曲强度可能存在较大的计算误差，具体论证如下。

采用有限元法建立R1、R2、R3 3组波板数值模型，具体几何参数见表1。3组模型中，板高为变数，其余的均为不变几何参数。其中R1组模型中，平子板宽度b与斜子板宽度c相等，R2、R3组模型中，b与c相差较大。

本工程位于浙江省乐清湾瓯江口港区，拟建一个岸线总长度为1250m、带有3个件杂货泊位、2个散货泊位、2个待泊泊位的综合码头，为后方钢铁厂输入原材料及输出件杂货钢材服务。根据地勘测量，需进行地基处理的区域约2.05万m²。实例工程土层分布情况见图1。

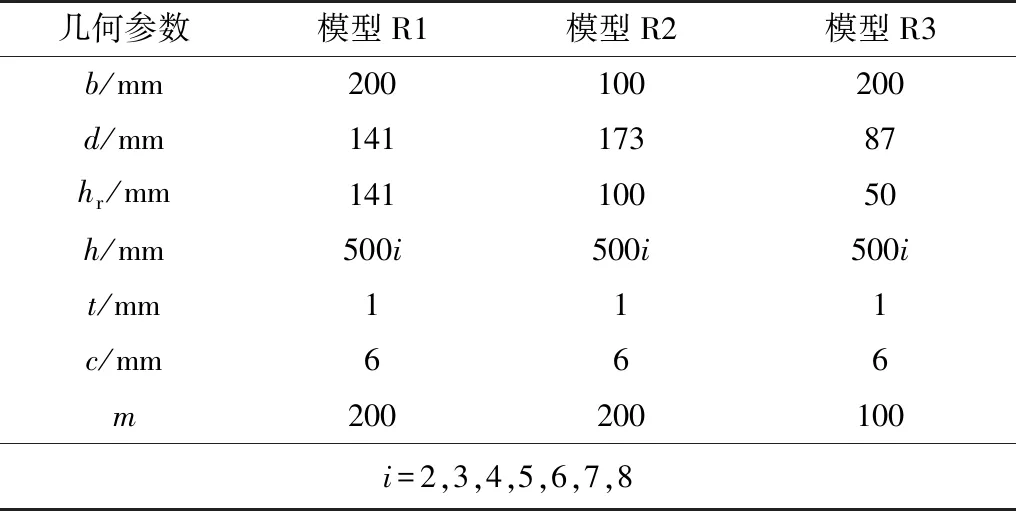
表1 几何参数Table 1 Geometric parameters

R1组模型的分析结果如图3，R2和R3组的分析结果如图4。

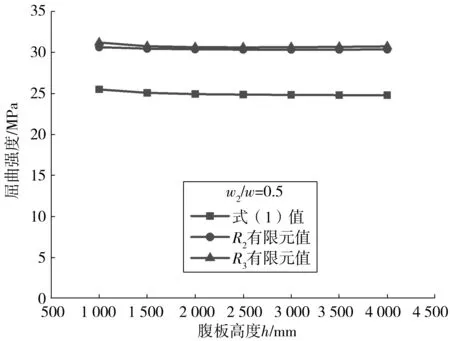
图3 模型R1屈曲强度计算结果Fig. 3 Calculation results of model R1 buckling strength

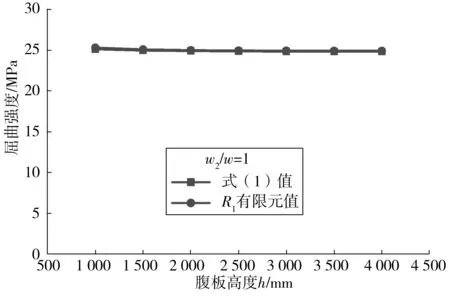
图4 模型R2、R3屈曲强度计算结果Fig. 4 Calculation results of model R2 and R3 buckling strength

由图3可见，平子板宽度b与斜子板宽度c相等的R1组模型中，FEM得出的屈曲强度与现有的计算公式(1)得出的结果几乎相等。由图4可见，b与c相差较大的R2、R3组模型中，FEM得出的屈曲强度远大于式(1)得出的结果。由此可判断现有计算公式不能适用于计算b与c不相等条件下的波板屈曲强度，其原因在于式(1)中只考虑了较宽子板宽度w=max(b,c)的影响，忽略了较窄子板宽度w2=min(b,c)的影响。

以R1组中h=2 000 mm的模型为例，其屈曲模态图见图5，其平子板屈曲模态与斜子板的屈曲模态基本上是相同的。若从图5中取一块子板，将该子板4个边设置为简支，用FEM对其进行分析可得弹性剪切屈曲模态图6，该屈曲模态和图5中的平子板屈曲模态相似。

图5 R1模型屈曲模态(τn,el =25.5 MPa)Fig. 5 Buckling mode of R1 model (τn,el =25.5 MPa)

以R2和R3组中h=2 000 mm的模型为例，其屈曲模态图见图7和图8，其平子板屈曲模态与斜子板的屈曲模态差异较大。该屈曲模态的特点在于较宽子板的屈曲占据主导，较窄子板基本不发生屈曲，但对较宽子板产生约束作用。由于该约束现象提升了屈曲强度，故图4中的FEM分析结果高于式(1)的计算结果。若从图7、8中将较宽子板取出，将该子板4个边设置为简支，用FEM对其进行分析可得弹性剪切屈曲模态图6，该屈曲模态和图7、图8中的较宽子板屈曲模态都有很大差异。比较图7和图8，尽管两者的几何外形不相同，但局部上看两者的屈曲模态实质上是基本相同的，因为两者的较宽子板宽度都为w=200 mm，较窄子板的宽度都为w2=100 mm。另外，由于R2和R3组中所有模型的w都为200 mm，w2都为100 mm，在图4中，两者的FEM分析结果基本相同。

通过以上分析可知，当平子板和斜子板等宽时，可以将波板简化单个子板进行分析，故按照现有公式(1)简化计算波板的弹性局部屈曲强度是合理的。而当平子板和斜子板不等宽时，不可以按式(1)进行简化计算，此时不仅要考虑较宽子板宽度w，还需考虑较窄子板的宽度w2的影响,才能获得更高的精度。

图7 R2模型屈曲模态(τn,el=32.0 MPa)Fig. 7 Buckling mode of R2 model(τn,el=32.0 MPa)

图8 R3模型屈曲模态(τn,el=32.1 MPa)Fig. 8 Buckling mode of R3 model(τn,el=32.1 MPa)

3 弹性局部屈曲修正公式

3.1 修正弹性局部屈曲公式

由上文分析可初步推测，当波形腹板中的平子板宽度b与斜子板宽度c不相等时，子板的窄宽比w2/w是影响弹性局部屈曲强度和屈曲模态的重要因子。以下将通过量化解析论证w2/w对屈曲系数的影响。建立了SQ1和SQ2两组有限元模型进行数值模拟分析，其中d和hr为变量，其它为定值，共有5×5×2=50个数值模型，如表2。数值解析结果如图9，其横轴取X=w2/w，纵轴取换算屈曲系数如式(2)。

(2)

表2 几何参数Table 2 Geometric parameters

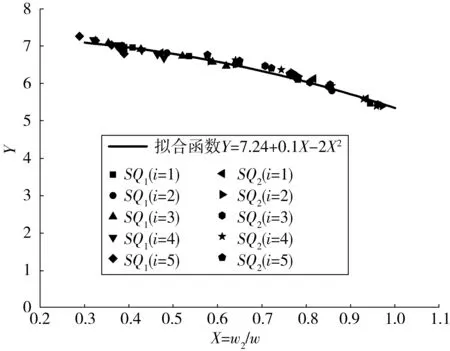
图9 拟合公式Fig. 9 Fitting formula

图9的解析结果反映出窄宽比X越小，换算屈曲系数Y越大的特点。当X接近于1时，Y接近于5.34，与四边简支平板屈曲系数的下限值相符。由于图9中的散点分散度很低，在窄宽比X=w2/w>0.3范围，X与Y具有很强的相关性，可用式(3)拟合函数表示。

Y=7.24+0.1X-2X2

(3)

由式(2)和式(3)可得局部屈曲强度的近似值为式(4)：

(4)

综上，在现有的弹性局部屈曲强度计算式(1)的基础上，考虑了窄宽比的影响，将其修正为式(4)，其适用范围为窄宽比w2/w>0.3。

3.2 算例和适用范围

首先选择板厚1 mm，屈曲模式接近于纯局部屈曲的下列尺寸模型进行有限元分析，对笔者提出的式(4)的适用性进行算例验证，具体尺寸模型及验证结果参见表3。

对于为窄宽比接近1的SL-1波板，式(1)的计算值与FEM计算值相近；但对于窄宽比远小于1的SL-2、SL-3、SL-4波板，式(1)的计算值与FEM计算值有很大差异。不论窄宽比为何值，笔者提出的式(4)得出的计算结果都与FEM计算值相符。

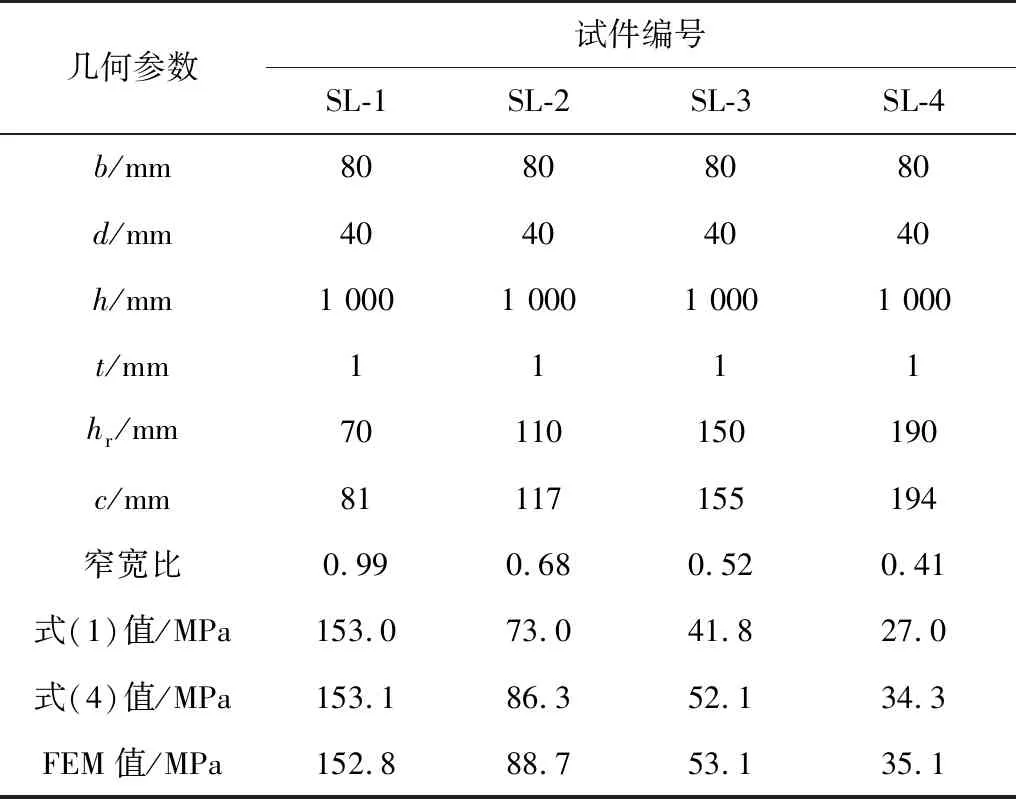
表3 算例结果汇总Table 3 Summary of the results

由于实际桥梁中的波板厚度一般在6 mm以上，不能完全按式(4)计算屈曲强度。以下建立t=6 mm，t=8 mm两组波板数值模型，分析式(4)的适用范围。具体几何参数见表4，两组模型中板高h=2 000 mm和波数m=6为定数，b、d、hr选为变量各有3个取值，进行组合可得3×3×3×2=54个数值模型。FEM的分析结果见图10。

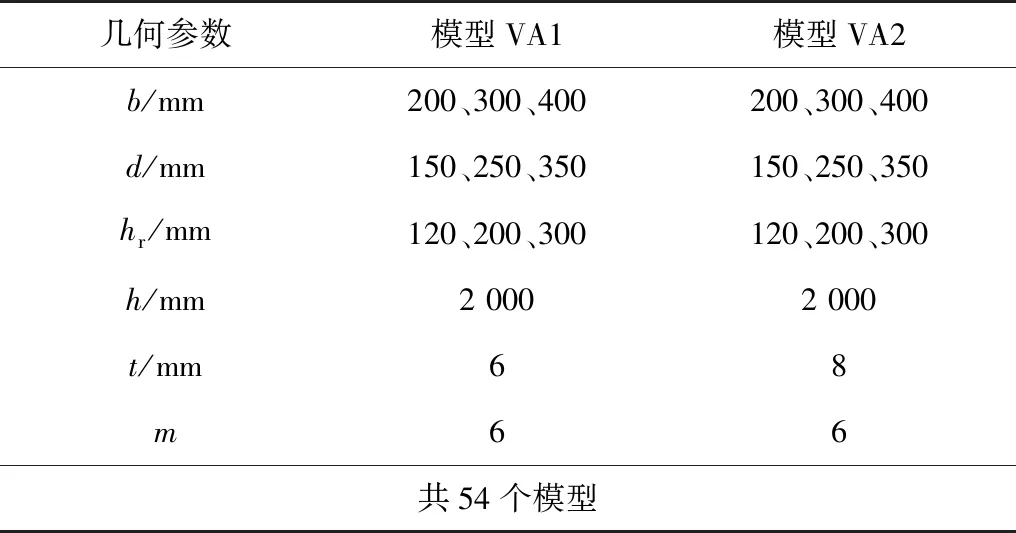
表4 几何参数Table 4 Geometric parameters

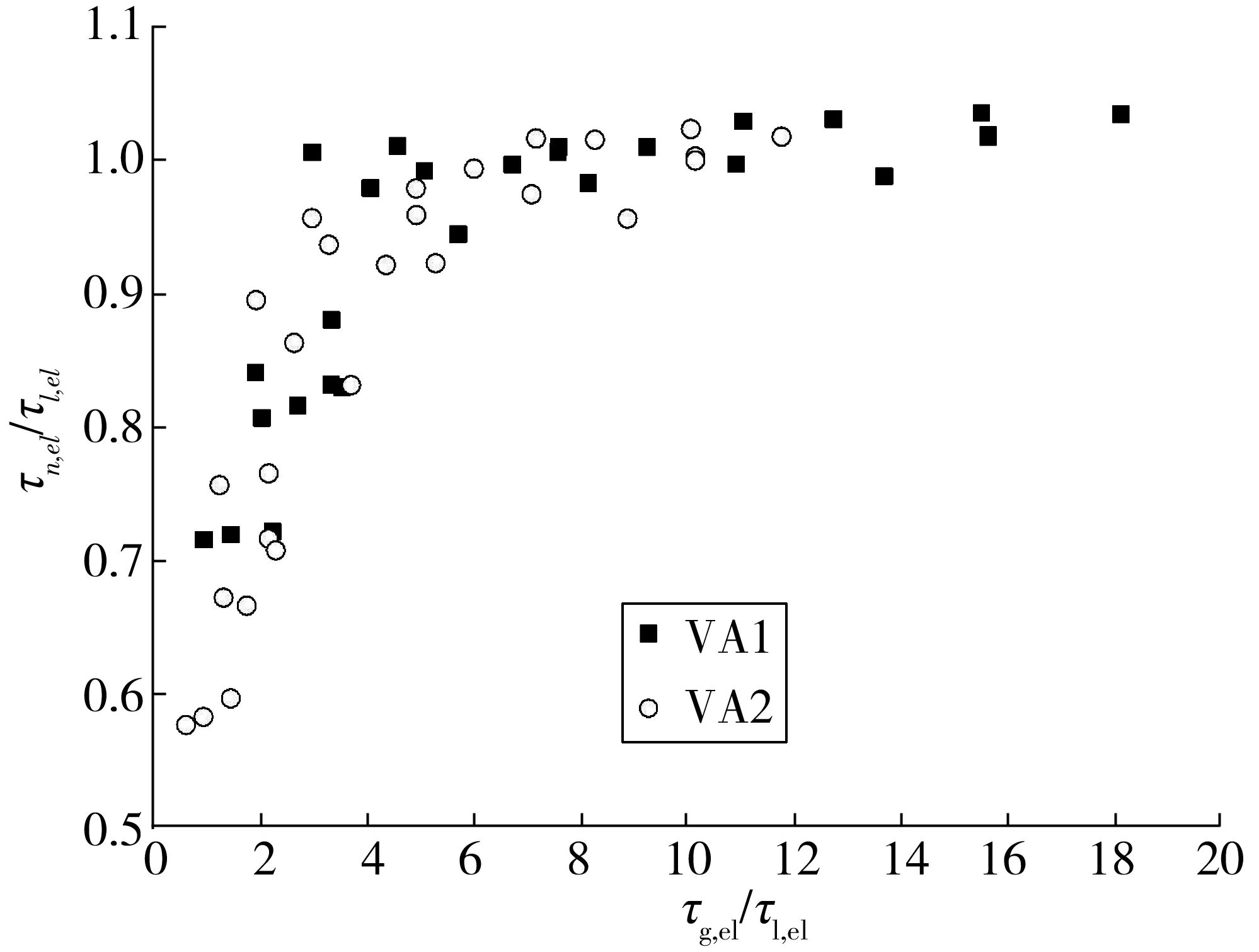
图10 适用性分析结果Fig. 10 Applicability analysis results

图10中，横轴取τg,el/τl,el，纵轴取τn,el/τl,el。τl,el为式(4)的计算值，τn,el为有限元分析得出的弹性屈曲强度，τg,el采用J. T. EASLEY[14]的整体屈曲强度计算公式为

(5)

(6)

(7)

由图10可见，当τg,el/τl,el>6时，τn,el与τl,el的比值在1附近，表明式(4)的计算精度较高。而当τg,el/τl,el<6时，式(4)的计算精度降低。比较VA1和VA2两组数据可以发现，厚度较小的VA1组模型中，满足τg,el/τl,el>6条件的模型数量更多。对于钢桥梁中板厚6 mm以上的波板，只要满足τg,el/τl,el>6条件，即可视为局部屈曲主导型波板，可以应用式(4)计算弹性屈曲强度。但τg,el/τl,el<6时，波板受整体屈曲以及合成屈曲的影响较大，式(4)不能适用。

4 结 语

结合有限元分析和参数分析的方法，对波板的弹性局部剪切屈曲进行研究。分析比较了不同几何参数的波板弹性局部屈曲强度以及屈曲模态的特征，发现弹性局部屈曲强度和屈曲特征主要取决于窄宽比。当窄宽比为1时，可将波板中的子板简化为单个四边简支的矩形平板；而当窄宽比不为1时，不可以简化，此时窄宽比是影响屈曲强度的重要因子。在现有的弹性局部屈曲强度计算式(1)的基础上，考虑了窄宽比的影响，将其修正为式(4)。通过算例论证，笔者提出的式(4)的适用性并不限于板厚1 mm的波板，也可适用于板厚6 mm以上的波板。式(4)的适用范围为：窄宽比w2/w>0.3、且τg,el/τl,el>6。

当窄宽比较小、板厚较大时，大部分波板将会出现τg,el/τl,el<6的情况，不能视为局部屈曲主导型波板，屈曲将转变为整体屈曲或合成屈曲，式(4)将失去适用性。在后续的研究中，还需继续讨论式(4)的更具体适用范围、整体屈曲强度以及合成屈曲强度等。