复杂水域船舶避碰路径规划研究
2019-12-17谢新连辛剑英
谢新连,何 平,何 傲,辛剑英
(大连海事大学 综合运输研究所, 辽宁 大连 116026)
0 引 言
船舶避碰一直是航海领域的研究热点,因为在运输过程中一旦发生碰撞事故,高价值船舶及其运输货物均会遭受损失,且碰撞事故会对海洋环境造成巨大的污染。避碰路径规划研究是实施船舶避碰的一个关键环节,因此研究船舶避碰路径极为重要。
船舶安全航行时需要避碰的目标主要分为静态障碍区和动态船舶。由于静态障碍区避碰问题较为简单,其研究相对较少,如:G.ANTONELLI等[1]介绍了一种具有实时路径规划并避开障碍物能力的航海诱导系统。目前,国内外学者对船舶避碰路径规划的研究主要集中于动态目标船舶上。如: CHANG Kiyin等[2]提出了一种能在栅格图中检测障碍物并进行障碍物规避的避碰路径规划算法;C.K.TAM等[3]利用已知的和预测得到的交通及环境数据,提出了一种近距离会遇船舶的路径规划算法;M.TSOU等[4]基于遗传算法,结合《国际海上避碰规则》(以下简称《规则》)和船舶安全领域来求取最短避碰路径,并提供了安全避碰转弯角度、复航时机及复航角度等参数;W.NAEEM[5]等基于《规则》提出了一种反应性的无人船避碰路径规划算法;XU Wen等[6]研究了在不考虑风、浪、流等因素下,利用动态船舶对开阔海域上航行的两艘船舶路径进行规划;C.TAM等[7]提出了一种满足《规则》的确定性避碰路径规划算法;林晓杰[8]利用改进势场法,结合船舶操纵及船舶领域等理论建立了受限水域中船舶的自动避碰模型;张树凯[9]等基于AIS航迹和Douglas-Peucker 算法实现了航线的自动生成,其能有效避开障碍物。
不难发现,鲜有学者对静态障碍区和动态目标船舶同时存在的复杂水域内船舶避碰路径规划问题进行研究。程细得等[10]用遗传算法对内河船舶及障碍区的避碰问题进行了分析;A.LAZAROWSKA[11]提出了一种基于蚁群算法的动态环境下避碰路径规划方法;M.TSOU[12]以ECDIS作为决策支持平台,结合PAD理论和《规则》,用进化算法来进行避碰路径规划。另外,现有研究规划出的避碰路径大部分是折线段路径,未考虑到船舶回转性能,无法保证船舶一定能按照规划出的路径安全航行。因此,笔者针对碍航障碍区和目标船舶同时存在的复杂水域避碰路径规划问题,在考虑《规则》前提下,利用预测危险区将目标船避碰转化为避让一个六边形区域(PAD),再利用船舶领域理论对障碍区进行缓冲区分析,并用切线图法对复杂水域进行环境建模,然后利用Dijkstra算法和改进的2-turn平滑方法进行了避碰路径规划。最后,通过仿真实验及对比实验予以验证。
1 复杂水域环境模型构建
1.1 复杂水域
复杂水域到目前为止仍没有一个明确的定义,通常是指自然条件差、船舶交通流复杂、船舶航行难度大的水域,包括海上施工水域、桥区水域、多航道交汇水域、航道弯曲段、航道狭窄段、浅滩航行区、坝区航段、锚泊区、渔船捕鱼水域、岛礁水域等。文中的复杂水域是指多个静态碍航障碍区和动态目标船舶同时存在水域。静态碍航区主要包括浅滩、暗礁、海岛、锚泊区等;动态船舶是指在海上正常航行且可能会影响我船安全航行的船舶。笔者研究的水域中同时包括了多个固定碍航障碍区和船舶会遇局面,因此,其复杂性不言而喻。
1.2 预测危险区
在本船保速情况下,通过对我船和目标船的航速、航向等进行预测处理,可得到可能碰撞点(PPC)的位置坐标,并作为避碰的决策依据。雷达测量和ARPA的跟踪处理往往存在误差,此外船舶本身的船型和大小对航行安全不可忽视,仅仅用可能碰撞点进行避碰决策是远远不够的。因此,在可能碰撞点基础上结合MIN CPA作图形成了预测危险区(PAD),如图1。在目标船保速、保向情况下,只要我船航迹避开预测危险区即可安全避开目标船。图1中:我船某时刻的位置为O点,航速为VO;目标船位置为T点,航速为VT;目标船相对航速为VR;PAD为图中的六边形。图2为基于MATLAB编程得到的PAD图,其中:我船航速为12 kn,航向角330°;目标船航速12 kn,航向角30°。
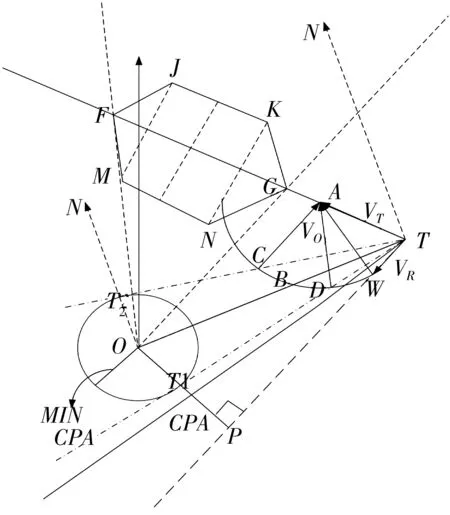
图1 PAD示意Fig. 1 PAD schematic

图2 预测危险区Fig. 2 Prediction of dangerous areas
1.3 缓冲区分析
由于船舶本身具有一定尺寸,且船舶正常航行需要满足一定的水深条件,故船舶不可能完全沿着碍航障碍区边界航行。此外,即使船舶能沿着碍航障碍区边界航行,由于浅水效应存在,反而会增大船舶与碍航障碍区发生碰撞的可能性。因此,为使船舶能安全地避开碍航障碍区,需对碍航障碍区进行一定的缓冲区分析。由于笔者未考虑风、浪、流等影响因素,故以文献[13]提出的船舶领域模型中的Rstarb长度作为基础缓冲距离,计算如式(1)、(2):
Rstarb=(0.2+KDT)×L
(1)
KDT=DT/L=100.544 1logV-0.079 5
(2)
式中:L为船长,m;KDT为旋回初径对船长的无因次化;DT为船舶回转直径,m;V为航速,kn。
另外,当船舶航行路径经过碍航障碍区之间水域时,船舶本身尺寸因素不可忽视。因此,笔者在Rstarb基础上增加0.5倍船长作为缓冲区,如式(3):
Rstarb=(0.7+KDT)×L
(3)
通过该处理,当船舶在碍航障碍区之间水域通行时,由于对每个碍航障碍区进行缓冲区分析时增加了0.5船长,即相当于对该水域增加了1倍船长缓冲区。因此可将船舶视为一个质点,便于后续路径规划。
1.4 切线图法构建环境模型
切线图法主要是通过求解起始点及终止点对所有碍航区(包括碍航障碍区及预测危险区)的切线及碍航区相互之间的公切线,从而构建一个关于起始点、终止点及需要避让的碍航区切线图网络环境,并通过该网络可进行初步局部最短航路的规划。文献[14]证明了平面上移动机器人局部最短路径由凸多边形碍航区域的边界和碍航区域之间的公切线组成。虽然船舶在海上航行时遇到碍航区不一定是凸多边形,但根据前面结论可知:即使是非凸多边形,其避碰局部最短路径与该非凸多边形对应凸包围盒(凸多边形)局部最短路径等同,均是从其边界点或沿边界线通过,如图3。
图3中:船舶从O点到D点过程中需避开一个非凸多边形。假设船舶的最短路径为OHGJD。HGJ构成一个三角形,由三角形的几何定律易知:HG与GJ的长度之和大于HJ长度,因此船舶最短路径应用HJ代替HGJ,即OHJD为船舶最短路径;即船舶避碰最短路径从该非凸多边形边界点的连线通过,证毕。因此,为便于处理,可用凸包围盒来代替非凸多边形,HJKLH即为原非凸多边形的一个凸包围盒(图3)。
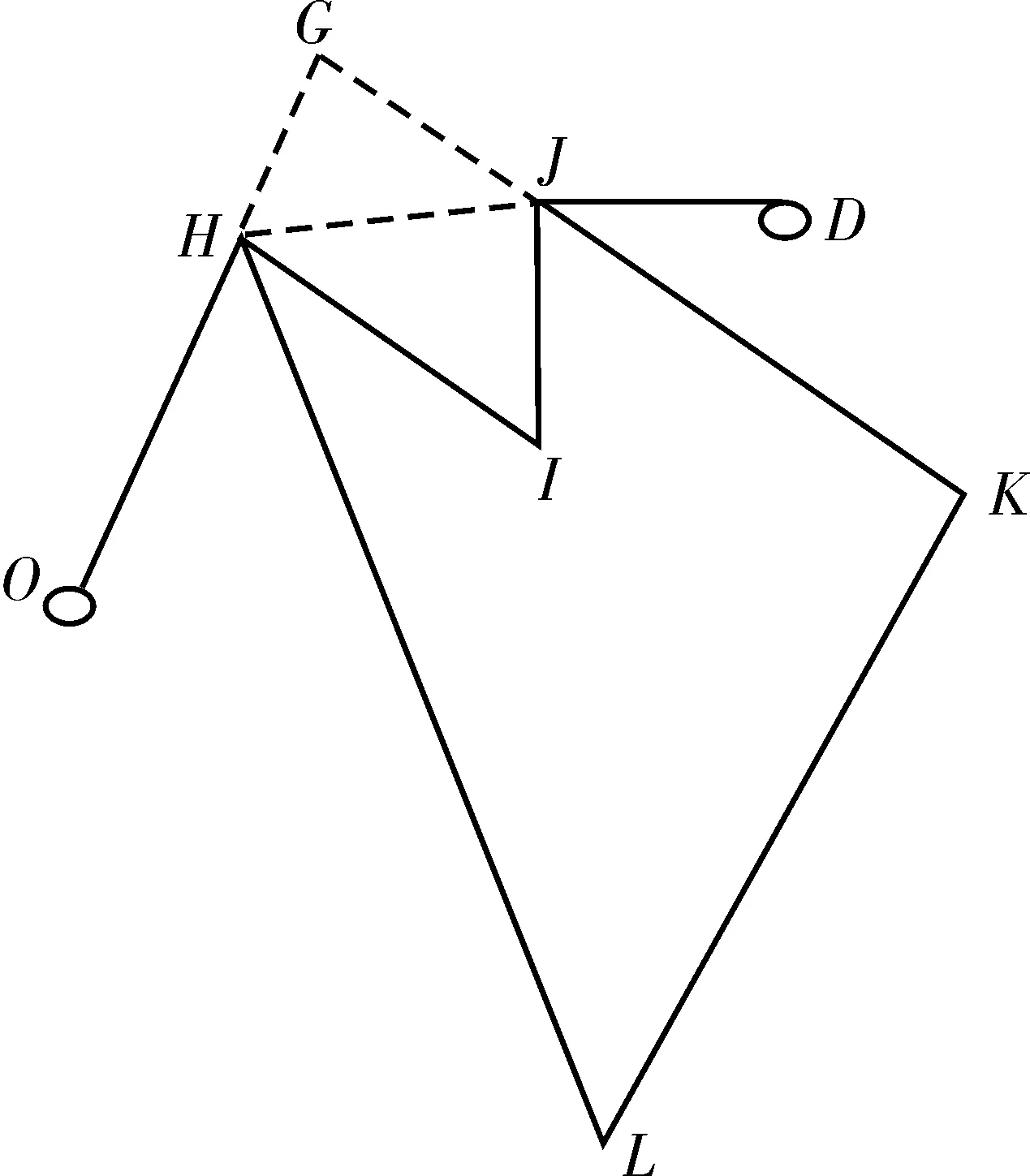
图3 非凸多边形最短路径Fig. 3 The shortest path of non-convex polygon
文中切线及公切线求取算法如下:
1)切线算法
Step 1:连接起点与终点生成一条探测线段;
Step 2:用集合M表示与探测线段相交的碍航区。若M为空,结束算法。否则,求起点和终点与M中碍航区的切线段,用集合N表示;
Step 3:若N为空,结束算法。否则,在N中任取一条切线段N1,判断其是否与碍航区相交。否,则将N1从N移入最终切线段集合R中,然后判断N中的下一条切线段;若与M之外的碍航区相交,则用M2表示该情况下的相交碍航区,并求起点、终点与M2中的每个碍航区的切线段L,再将L放入N中并删除N1,将M2移入M中,返回Step 3。
2)公切线算法
Step 1:提取求切线段过程的M集合;
Step 2:若M中碍航区数小于1,结束算法。否则,求M中任意两个碍航区之间的公切线段,得到公切线段集合N;
Step 3:若N为空,则结束算法。否则,在N中任取一条切线段N1,判断其是否与碍航区相交。否,则将N1从N移入最终切线段集合R中,然后继续判断N中的下一条切线段;若与M之外的碍航区相交,则用M2表示该情况下的相交碍航区,对所有M与M2中的碍航区m和m2,求m与m2间以及M2中任意两碍航区间的公切线段L,并求起点、终点对M2的切线段L1,将L及L1移入N并删除N1,将m2移入M中,返回Step 3。
通过以上切线及公切线的求取算法,可求得如图4中的碍航区切线网络。
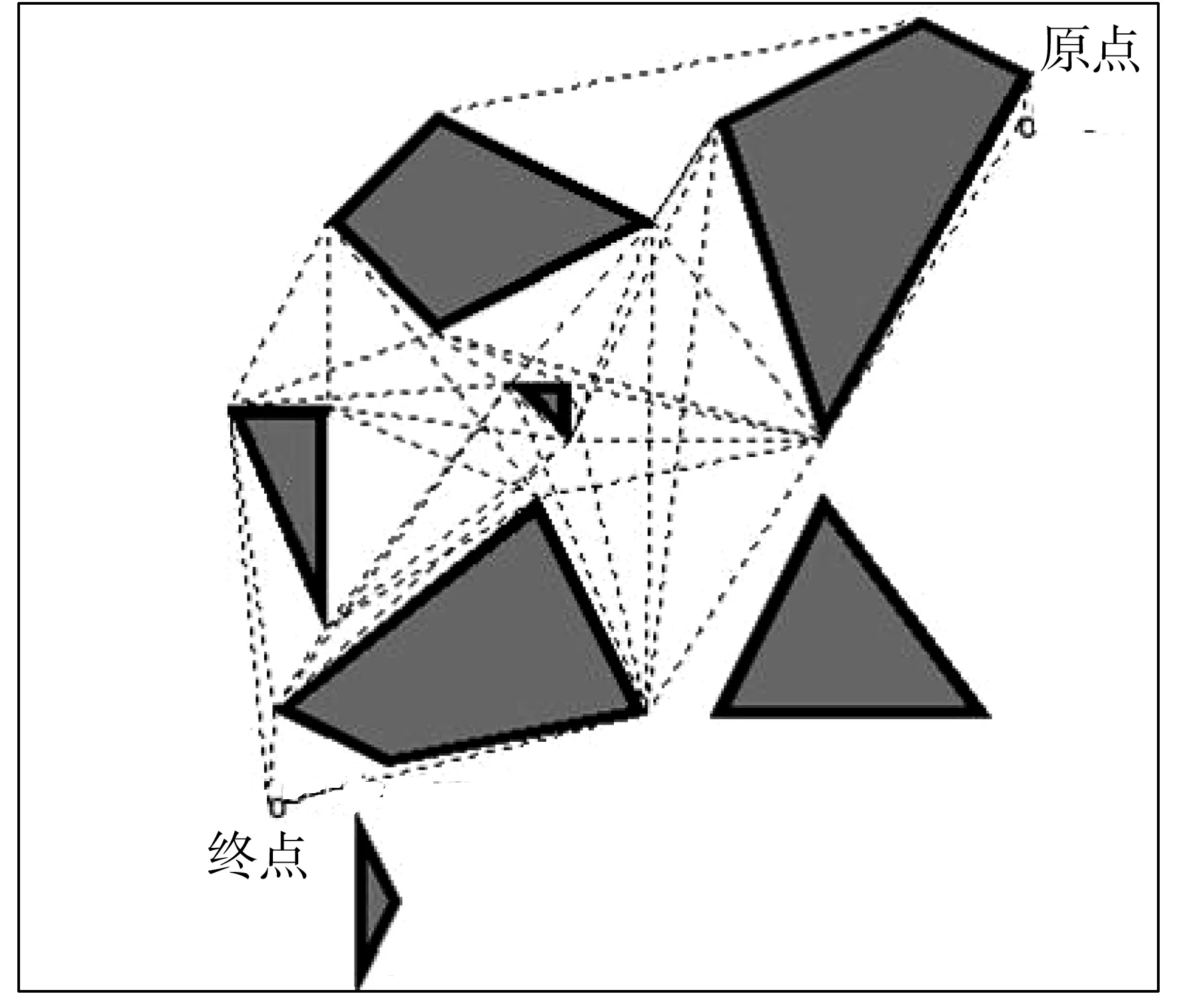
图4 切线网络Fig. 4 Tangent line network
2 路径规划
2.1 初步路径规划
上述切线及公切线求取算法不但可求得切线网络,还可求得每条切线段端点坐标,并判断哪些碍航区是船舶需要避让的。相对于直接对所有碍航区求取切线的算法,该方法时间复杂度更小。起点、终点及需要避让的碍航区顶点构成了避碰路径点集合。通过求切线段的长度及需要避让的碍航区中各边界线长度,则可求得路径点集合构成的距离矩阵。对于图4中的切线图网络,可求得类似式(4)的距离矩阵。由于该距离矩阵只考虑了起止点及航行时需要避碰的碍航区顶点,未考虑不需要避碰的碍航区顶点,因此能减少算法时间复杂度。

(4)
通过式(4),用Dijkstra算法可求得如图5的初始路径。

图5 初始路径Fig. 5 Initial route
2.2 路径平滑
船舶路径规划不同于机器人路径规划,机器人路径可以为折线,但船舶路径不行。为使船舶航行更加符合实际及动力学要求,需对Dijkstra算法求得的折线路径进行平滑处理。
目前路径平滑方法主要有:多项式最小二乘拟合、曲线拟合(如贝塞尔曲线、B样条曲线)、平滑蚁群算法和笔者使用的2-turn平滑法等[15-16]。在进行船舶避碰路径平滑处理时,需考虑以下几点:船舶回转直径、平滑后路径与初始路径之间的总长度偏差(偏差要尽可能小)、平滑后路径不能与碍航区域相交(只能相切或相离)。2-turn平滑法能很好满足这些条件,因此笔者采用2-turn法进行平滑处理。
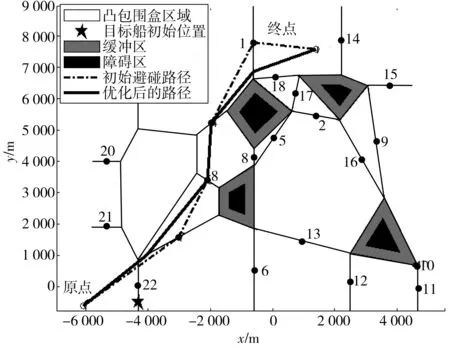
2-turn平滑法的主要思想是:对相邻两个折线路径段,用两个外切圆来进行平滑处理,这两个外切圆彼此之间也相切,如图6。图6中:O1与O2分别为两个外切圆的圆心;S1与S3分别为两个外切圆与原路径切点;S2为两个外切圆交点;d为路径段2的长度;L为线段S1S3长度;θ和δ分别为船舶在两次转向过程中的航向改变量,称第一次航向改变量为避碰转弯角度,第二次航向改变量为复航角度。
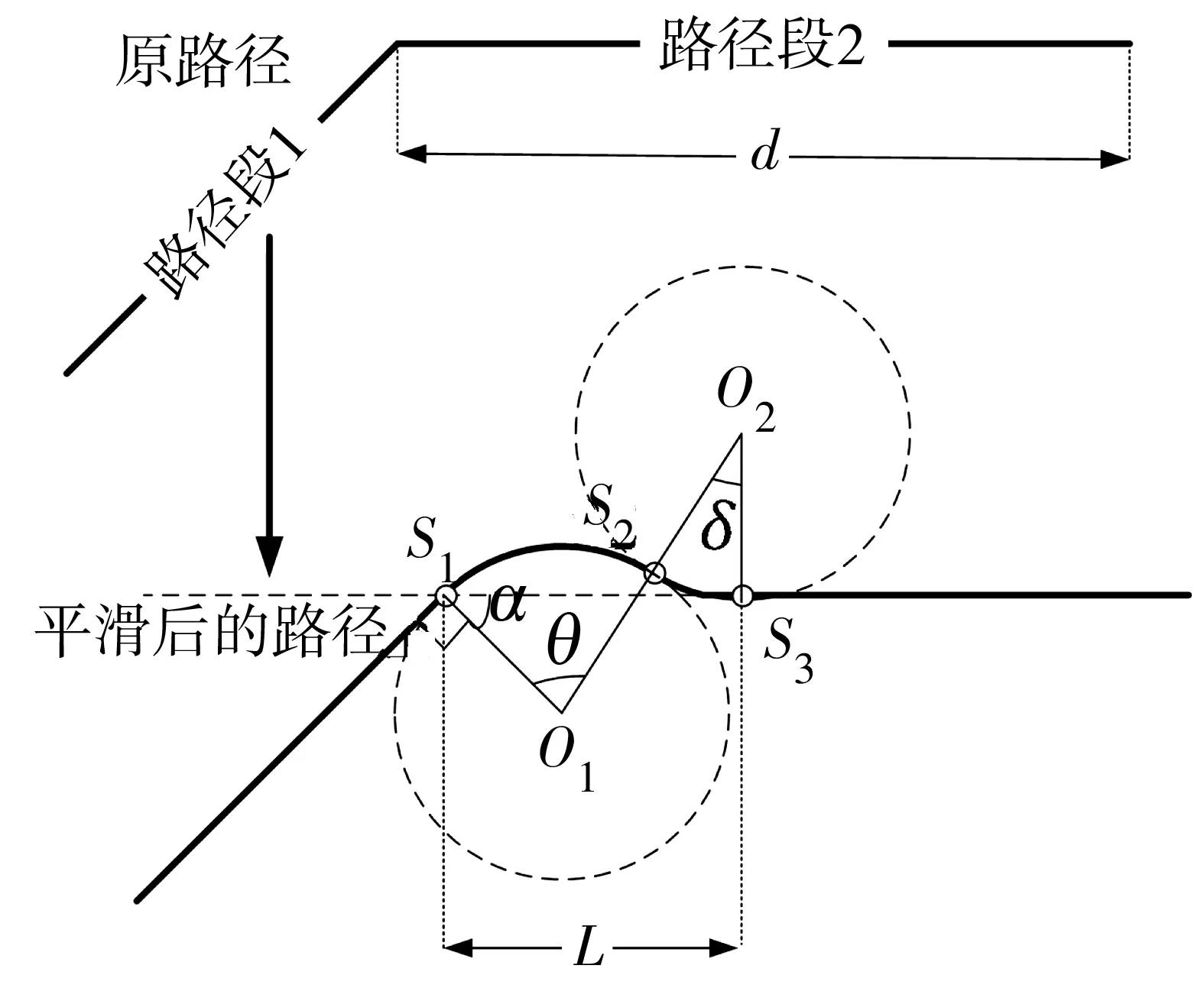
图6 路径平滑Fig. 6 The smoothness of route
由于利用2-turn方法进行平滑处理时利用的是船舶回转直径,因此其路径平滑部分曲线直径必须大于船舶最小回转直径。此外,若利用最小回转直径求得的平滑路径中S1与S3两点组成线段长度大于路径段2长度,则说明船舶不能够在此处完成转向操纵,则该路径规划不合理,有碰撞危险。此时,需要将路径段2所在切线段删除,并重新进行路径规划。笔者选取季美(Thieme)公式[17]作为船舶的最小回转直径,如式(5):
D=0.25L5/3
(5)
基于2-turn思想,结合船舶航行实际,笔者给出以下改进路径平滑算法:
Step 1:根据当前航速和欲转向舵角来确定回转直径D,进而确定D对应的半径R;
Step 2:根据S1坐标和半径R大小可确定第一个外切圆的圆心O1;
Step 3:根据O1与O2之间的距离为2R,且O2点到路径段2所在直线的距离为R,确定O2点坐标;
Step 4:根据上述结果可得出两个外切圆O1与O2方程,联立该方程可得交点S2坐标;联立O2与路径段2直线方程可得S3坐标;
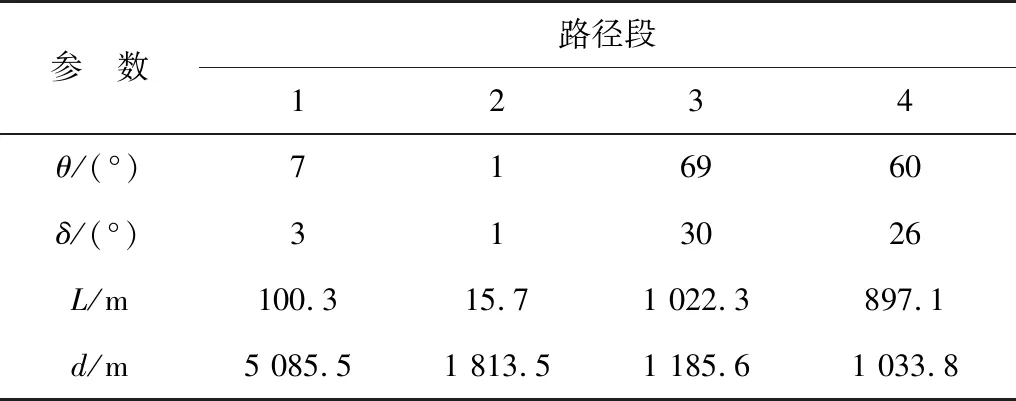
Step 5:计算L长度(L=Rcosα+2Rsinδ)。若L Step 6:根据以上结果,画圆弧S1S2和圆弧S2S3; Step 7:用圆弧S1S2和圆弧S2S3以及半径R的长度 来计算避碰转弯角度θ及复航角度δ。 对Dijkstra算法求得的初始路径进行平滑处理,得到路径如图7。 图7 最终路径Fig. 7 The final path 为进一步验证文中方法的正确性及有效性,笔者用仿真案例进行实验,并用MATLAB进行仿真计算。其中:船舶以及碍航区位置坐标采用平面直角坐标系方法表示,路径图中的横轴表示x坐标,纵轴表示y坐标,坐标单位为m。障碍区顶点坐标如表1。 表1 障碍区位置信息Table 1 Location information of obstacles 我船的基本参数如下:油轮,总长为122 m,船宽18 m,满载吃水8.5 m,舵面积比约为1.4%。现有一组我船航速为6 m/s,轻载状态下操不同舵角的旋回直径数据,见表2。 表2 不同舵角下的回转直径Table 2 Turning diameter at different rudder angles 由表2可知:该船在此情形下的回转性能较差。因此,用其进行算例分析可以充分验证该路径平滑处理对于操作性能较差的船舶也具有较好的实用性。因为操纵性能优良的船舶在克服转弯过程中所产生的误差要远小于操纵性能差的船舶,因此采用操纵性能差的船舶进行计算,对于算法的验证更具备说服力。 我船某时刻的位置坐标为(-6 081.2, -614.09),目的地坐标为(1 005, 7 053),航速6 kn,航向角30°。利用式(3)可求得:Rstarb=355 m。目标船的船长为171 m,其某时刻位置坐标为(-4 299.2,-497.27),航速6 m/s,航向角0°。根据《规则》,我船为让路船,需要“早、大、宽、清”地履行避让目标船义务[18],由于要结合PAD来履行我船让路义务,而PAD要求我船保速,因此我船采用转向避让的措施来避碰目标船。此情形下PAD区域与碍航障碍区4有重叠部分,构成一个非凸的多边形,如图8。需先求其凸包围盒,再进行路径规划。 采用文中算法,并以舵角为10°、航速为6 m/s对应回转直径来进行路径平滑,可规划出如图9的避碰路径。另外,转向过程中不考虑船舶回转运动中的反横距,并以阶跃操舵方式进行转舵。路径平滑处理后得到的参数如表3。由表3可知:第一个和第二个平滑段航向改变量较小,说明前后路径段近乎平行。所有平滑处理中的L均小于d,说明规划的路径符合船舶航行实际。由于表3中最大回转直径能满足路径平滑要求,因此可得知船舶在转向时,可采取舵角在[10, 35]之间。同样,基于Maklink图可求得最优避碰路径,如图10。文中方法运行时间为0.21 s,最短路径长度为11 514 m;基于Maklink图法运行时间为2.13 s,最短路径长度为11 727 m。 图8 碍航区发生重叠Fig. 8 Overlapping of navigation-obstruction areas 图9 切线图法的避碰路径Fig. 9 Collision avoidance route of tangent line method 表3 平滑路径段的参数Table 3 Parameters of smoothing routes 图10 Maklink_蚁群算法的避碰路径Fig. 10 Collision avoidance route of Maklink_ACO method 通过实验可证明笔者提出的避碰路径规划方法正确性。此外,通过与基于Maklink链接图法的路径规划算法进行对比,可以发现文中方法在时间性能、路径整体平滑性和最短路径长度上均更优,且由于笔者的路径规划完全基于几何以及计算几何等确定性理论和算法,其计算出路径无需用智能优化算法再进行优化计算,因此每次计算得到的路径是相同的且为最优路径,其路径唯一性是其他方法所不具有的。此外,由于该算法中路径平滑考虑到船舶不同航速、舵角下的回转直径因素,其平滑处理之后不仅更加符合船舶航行实际,还能给出避碰转向角度和复航角度并能检验规划路径是否能保证船舶安全、航行。由于该方法决策时间很短,可有效地应用到现有的电子海图显示中,并与信息系统(ECDIS)等平台综合进行避碰辅助决策。 笔者结合《规则》,考虑船舶航行中的不同舵角、航速下的回转直径、路径的平滑性等因素,提出了一种能够解决目标船和碍航障碍区同时存在的复杂水域避碰路径规划的方法。 相对于其他方法,其优点为:时间性能更好、路径整体平滑性好、路径优化程度更高、路径具有唯一性、能给出避碰转弯角度及复航角度、能检验规划的路径是否能够保证船舶安全航行。因此,可将其应用到现有的电子海图显示及信息系统(ECDIS)等决策平台中,从而可为该类复杂水域的船舶避碰决策提供辅助支持。 笔者对目标船进行处理时,以目标船保速、保向且我船保速为前提。实际中还存在目标船速度大小、方向及我船航向发生改变等情况,此时需要更新原预测危险区,再重新计算避碰路径,从而可实现动态的避碰路径规划。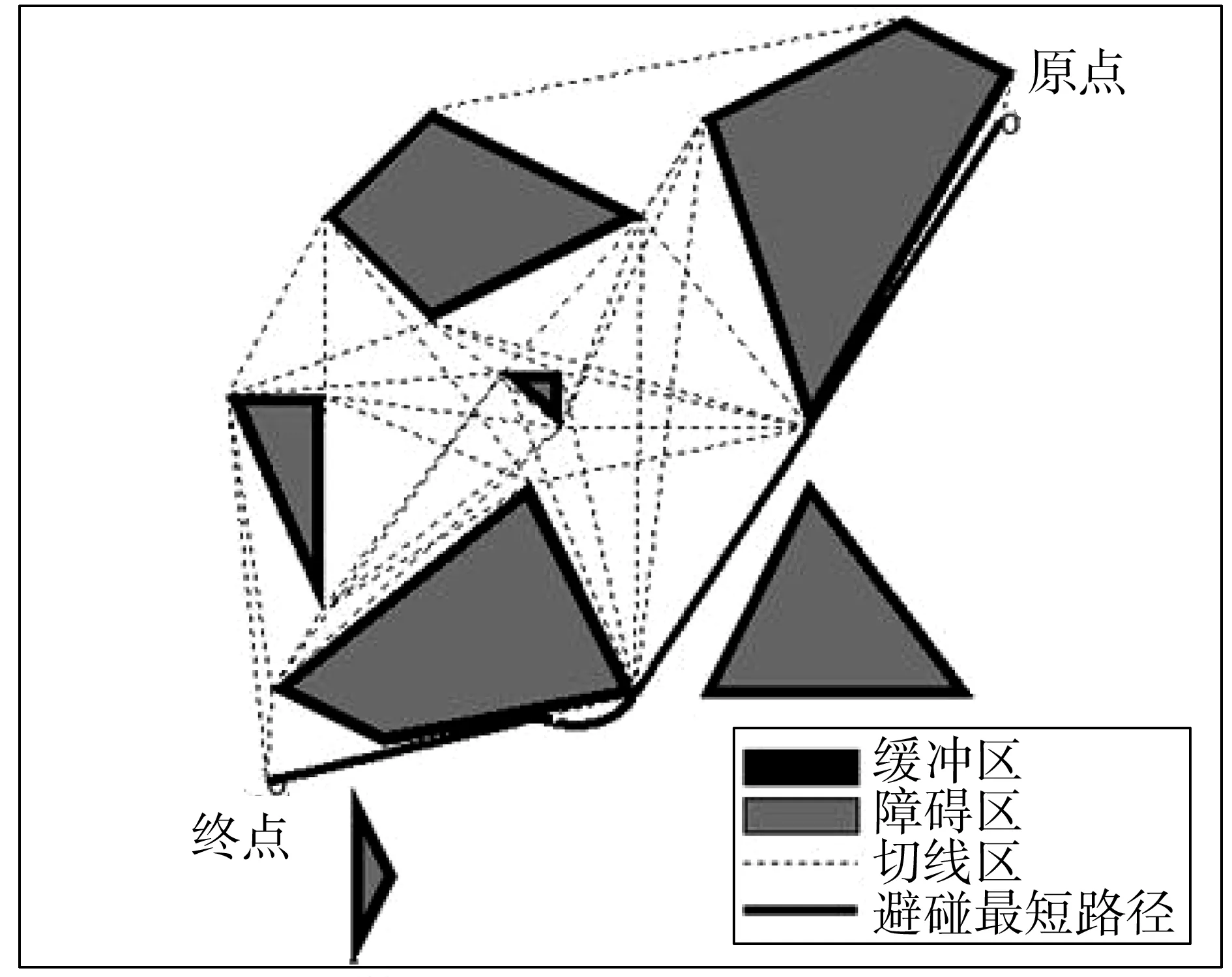
3 仿真实验

4 结 语
