高速铁路连续梁拱桥拱梁竖向刚度比对结构性能影响的研究

2019-12-17郝礼增马坤全郭玉坤

石家庄铁道大学学报(自然科学版) 2019年4期

郝礼增，马坤全，郭玉坤

（1．同济大学桥梁工程系，上海 200092；2．中国铁路上海局集团有限公司建设管理处，上海 200071）

0 引言

连续梁拱组合体系桥梁是一种结构受力合理、跨越能力强、外形美观的结构体系，其综合了连续梁桥和拱桥的受力特点，被广泛应用于公路、铁路桥梁建设中。从受力体系上分析，连续梁拱桥主要通过连续梁直接承担荷载，通过吊杆将一部分荷载传递到拱肋，并通过主梁内布置的纵向预应力体系平衡拱脚水平推力，达到拱-梁共同受力的状态。在拱梁组合体系桥梁设计中，拱梁的刚度比对结构受力、动力特性、稳定性以及施工方案有较大影响，设计中应根据具体情况，合理选择拱梁的刚度，以达到最优的设计［1］。拱梁组合体系桥中拱的刚度一般指拱肋的抗弯刚度，梁的刚度指桥面参与系梁共同作用的抗弯刚度，拱梁刚度比一般认为是拱结构和主梁结构的抗弯刚度比值，即EI拱／EI梁。梁拱组合体系根据拱肋与梁（系杆）相对抗弯刚度的大小可分为柔梁刚拱、刚梁柔拱和刚梁刚拱3种，一般认为EI拱／EI梁＜1／80为刚梁柔拱，EI拱／EI梁＞80为柔梁刚拱，EI拱／EI梁介于1／80和80之间为刚梁刚拱［2］。对于工程上比较常见的钢管混凝土拱肋，可以采用钢混模量比将其换算成钢（或混凝土）等效截面［3］，变截面连续梁可以按挠度理论将变截面换算为等截面［4］，具体方法为模拟跨径布置与原方案相同的等截面连续梁，在相同的竖向均布荷载作用下，主跨跨中挠度相等时，等截面连续梁的抗弯惯矩即可作为原方案的换算等量惯性矩［5］。

为配合连续梁拱桥的结构设计，国内外学者开展了拱梁刚度比对结构受力特性的影响研究。王洪超［6］探讨了矢跨比、梁拱刚度比等参数对预应力连续梁拱组合桥内力的影响，并分析了抗弯刚度改变时，构件截面积不变和同步改变2种情况的结构内力，给出了抗弯刚度比的合理取值范围。李映［1］介绍了3座不同的拱梁组合体系桥梁的设计实例，并对拱和梁的相对刚度进行了分析，探讨了拱梁相对刚度对全桥结构受力的影响。周冬［7］以温福铁路昆阳特大桥为背景，用力学解析法研究了连续梁拱组合结构的梁拱协作机制，定量地求出了梁拱分担弯矩比和拱肋分担荷载比，并讨论了梁拱抗弯刚度比、矢跨比等参数对二者的影响。黄夏雨［8］结合九曲江特大桥工程，分析了钢管混凝土体系和梁拱组合体系的建模分析思路、关键边界条件的处理和施工阶段的划分，并研究了梁拱刚度比对简支体系动力特性的影响。孙川［9］针对资阳沱江特大桥结构构造特征，使用ANSYS建立有限元模型，分析了拱肋刚度、横撑刚度、预应力度对结构动力特性的影响。耿鹏智［10］结合宜兴市梅林大桥工程，考虑了边跨与中跨截面形式不同的情况，利用结构力学方法推导出了连续梁拱组合体系拱肋分担荷载计算公式，并分析了包括拱梁抗弯刚度比在内的结构总体布置参数对结构受力的影响。刘忠平等［5］保持主梁刚度不变，通过改变拱肋刚度，研究拱梁刚度比对铁路大跨度连续梁-拱组合桥主梁、拱肋内力的影响。向金枭［11］以新津河大桥为工程背景，在主梁和拱肋均为等截面形式的假定下，通过工程力学方法求解了拱肋承担连续梁的荷载比，拱肋拱顶的挠度、轴力及弯矩，以及连续梁中跨跨中的挠度和弯矩，并讨论了连续梁和拱肋抗弯刚度比的影响。

上述学者对刚度比影响的研究得到了一个基本相同的结论，在保持拱肋和主梁截面面积不变的情况下，拱梁刚度比对结构轴力影响较小，对拱肋弯矩影响较大，主跨拱肋荷载分担比例受边跨主梁影响较小。在结构刚度定义方面，通过抗弯刚度定义的拱梁刚度比虽简洁明了，计算过程清晰，但在拱梁组合结构中，拱肋是以承压为主的压弯构件，拱结构的承载能力还与拱轴线形、拱脚边界条件等有关。这种定义只是简单地将拱和梁的抗弯能力进行比对，忽视了拱的承压能力等其它因素对结构受力特性的影响，不能真实反映结构刚度。其次，在结构方案拟定方面，多数研究采用假定某一部分刚度不变、调整另一部分刚度的方式产生比对方案。这种方案拟定思路对于讨论同种荷载在梁拱中分担比例的问题，具有较为理想的效果；但在分析探讨结构受力和变形特性以及结构动力特性等方面，由于结构总刚度的不同，各方案就不具有可比性。此外，在拟定的结构方案中，大多采用直接修改拱或梁的抗弯惯矩EI的方式来实现拱梁抗弯刚度比的调整，或者改变钢材型号或混凝土标号等，但由于在实际工程中很难实现在不改变截面面积的条件下调整抗弯惯矩，方案并不具有可操作性，而且结构变形能力不只与抗弯刚度有关。因此，通过调整拱肋和主梁截面形状和尺寸的方式实现拱梁刚度比的变化则更为合理、可行。

为此，综合考虑了结构产生变形的因素，较为精确地定义了拱梁组合体系的拱梁刚度比，并按照统一主梁主跨最大竖向挠度的原则拟定结构方案；参考徐盐铁路后马庄特大桥连续梁拱桥的设计，分析讨论拱梁刚度比对结构性能的影响。

1 结构刚度定义

在力学基本原理中，刚度的定义为“结构抵抗变形的能力”，通过单位变形产生的抵抗力来描述。以此概念定义结构拱梁刚度比：拱肋竖向刚度K拱即为在拱顶作用的集中力P拱与拱顶竖向位移δ拱的比值；主梁竖向刚度K梁为在连续梁主跨跨中作用的集中力P梁与主跨跨中竖向位移δ梁的比值；拱梁刚度比则定义为拱肋竖向刚度与主梁竖向刚度之比值K拱／K梁。这种定义既包含了已有同类研究中考虑的抗弯能力对结构刚度的影响，也考虑到了结构抗压、抗剪等其它方式抗力的贡献；在实际计算中，结构边界条件和线形因素对刚度的作用也能得到体现。因此，采用该方式定义的拱梁刚度比可以更加真实体现结构的刚度特征。

若主梁为等截面梁（抗弯刚度为EI，主跨跨径为L，边中跨比为μ），主梁刚度计算式为

若拱肋为等截面圆弧拱（半径为R，总圆心角为θ，截面抗弯刚度为EI，抗压刚度为EA），假定拱脚为固结时，可按照下式计算刚度

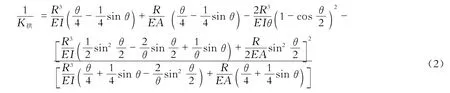
2 工程概况

徐宿淮盐铁路跨徐淮高速公路后马庄特大桥主桥采用预应力混凝土连续梁与钢管混凝土拱组合结构，设计时速250 km，跨径布置为（100+200+100）m，在国内同类桥梁中跨度最大。主梁除0＃块和拱脚采用C60混凝土外，其余梁段均采用C55混凝土悬浇箱梁，单箱双室布置，主跨跨中梁高6 m，桥面宽度14．2 m，顶板厚0．43 m，底板厚0．4 m，腹板厚0．4 m；中支点附近桥面局部加宽到14．8 m，梁高12 m，顶板厚0．62 m，底板厚1．1 m，边腹板厚0．9 m，中腹板厚1．0 m。拱肋为矢跨比1／5的等截面哑铃型钢管混凝土拱肋，拱轴线采用二次抛物线，设计拱轴线方程y＝-1／250x2+0.8x。钢管采用Q345qD 钢材，直径1．2 m，拱肋总高3．2 m，上下钢管通过缀板连接，钢管内和缀板之间均灌注C50补偿收缩混凝土；两片拱肋间距13 m，通过8组横撑连接。主跨共设置40组吊杆，吊杆间距9 m，每组吊杆采用2根PES（FD）7-61平行钢丝。全桥采用“先梁后拱”法施工。

3 连续梁拱组合体系桥拱梁竖向刚度比

表1为我国已建或在建大跨度铁路连续梁拱桥拱梁相对刚度。

表1 大跨度铁路预应力混凝土连续梁拱桥拱梁相对刚度

由表1可知，已建成或在建的12座主跨为116～180 m 客运专线连续梁拱组合体系桥拱梁刚度比均在0．5～2．0之间；在建的徐盐铁路连续梁拱桥拱梁刚度比仅为0．143，可归类为强梁弱拱桥（连续梁柔性拱桥）；在建的徐连高铁东海特大桥主桥拱梁刚度比达到11．512，可看作强拱弱梁桥。

4 方案拟定

在选取比对方案的时候，采用同步改变主梁和拱肋截面尺寸（或截面形式）的方法，生成不同刚度比的结构方案。为使方案具有可比性和可操作性，并确保结构刚度满足高速列车走行性要求，以徐宿淮盐铁路跨徐淮高速公路后马庄特大桥连续梁拱桥为基准，以静活载（ZK 荷载）作用下主梁主跨跨中竖向挠度相近（正负偏差在10%以内）为原则，拟定不同拱梁刚度比的连续梁拱组合体系结构。

表2为拟定的不同拱梁刚度比连续梁拱桥方案主要参数。各方案跨径布置均为（100+200+100）m，主梁梁底下缘均按圆曲线变化；箱梁截面型式、顶底板厚度和梁宽等构造尺寸、吊杆型号和布置以及拱肋矢跨比等均与后马庄特大桥（表2中方案3）相同；图1和图2为方案5和方案7的拱肋断面示意图。

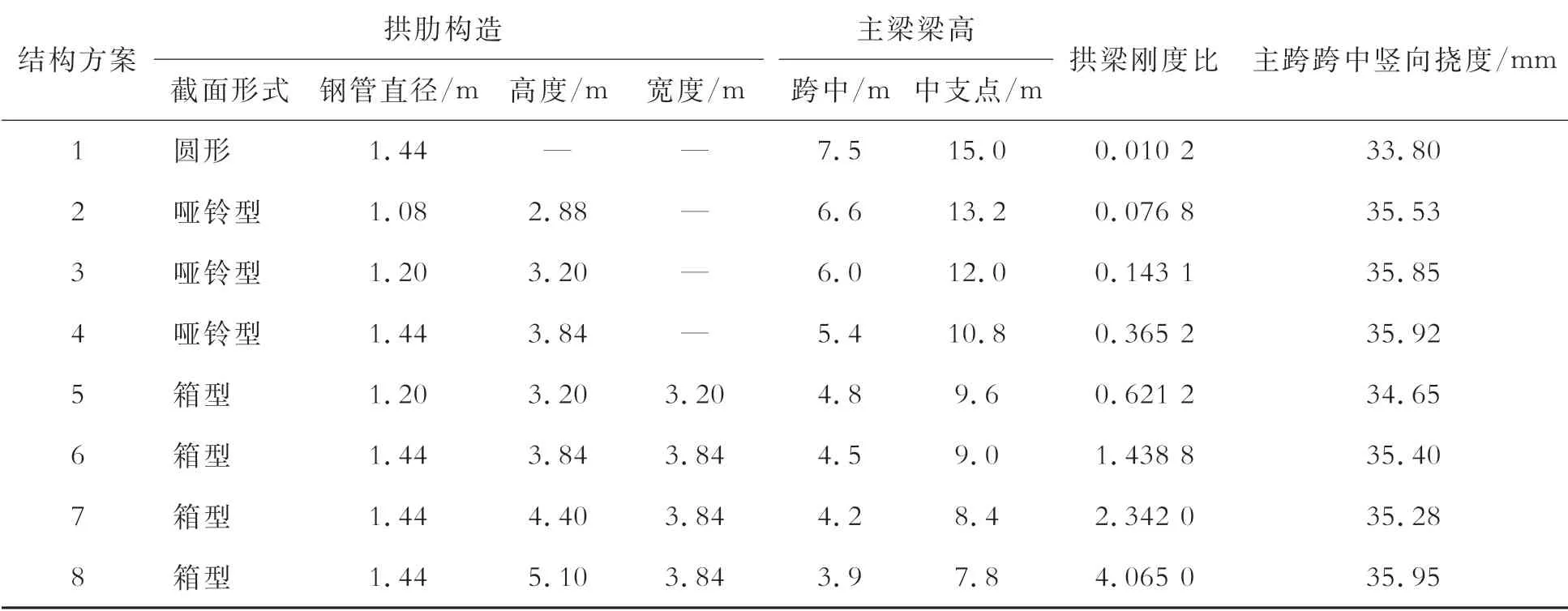
表2 连续梁拱桥方案主要参数

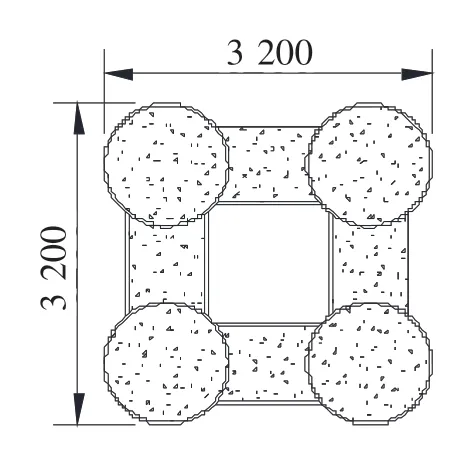
图1 方案5拱肋断面示意（单位：mm）

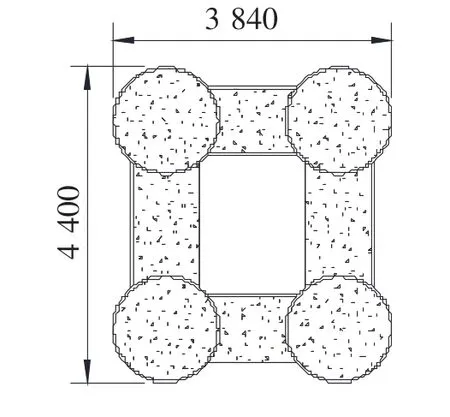
图2 方案7拱肋断面示意（单位：mm）

图3 徐盐铁路后马庄特大桥连续梁拱桥计算模型

5 计算模型

图3为采用Midas／Civil软件建立的徐盐铁路后马庄特大桥连续梁拱桥有限元计算模型，共379个节点，430 个单元。主梁采用变截面梁单元，横隔板部分单独建立1 个单元模拟；拱肋采用等截面梁单元，拱脚部分单独划分单元，截面特性采用施工阶段联合截面模拟，并通过弹性模量换算的方式将钢管内灌注的混凝土和拱脚外包的混凝土等效为Q345qD 钢材；吊杆采用只受拉桁架单元模拟，并将1组吊杆（2根）合并成1个单元；拱肋横撑只模拟横桥向的4根600（δ12）钢管。主梁和拱肋单元按照施工节段长度划分，并在主梁横隔板处、吊杆与梁拱连接处、截面变化较大处等位置适当加密。梁拱、吊杆两端与主梁和拱肋间均采用刚臂连接；根据支座的实际布置方式对结构施加边界约束条件，即在单个中支点约束主梁纵向位移，所有支点均约束主梁横向和竖向位移。

分析考虑二期恒载和移动荷载作用。二期恒载取为180 k N／m，沿桥长方向全桥布置；活载采用ZK荷载，双线加载，按照文献［12］计算的冲击系数为1．0；计算结构静活载竖向挠度和活载作用下控制截面内力的荷载工况为每个节点对应的最不利荷载布置；计算拱肋分担荷载比的活载工况为全桥满布双线ZK 荷载，集中荷载位于主跨跨中。

6 刚度比影响分析

6.1 结构刚度分析

表3、表4分别为结构静活载竖向挠度、动力特性计算结果。

表3 结构静活载作用下最大竖向挠度

表4 主梁竖向自振特性

由表3可看出，随着拱梁刚度比增大，边跨挠度较快增加，在拱梁刚度比增加到一定数值后（如方案4，其拱梁竖向刚度比为0．365 2），主梁边跨挠跨比即大于主跨，结构竖向刚度将由主梁边跨刚度控制；因此，在增大拱梁刚度比的同时，宜采取减小边中跨跨径比、增大主梁边跨截面尺寸等措施提高主梁边跨的刚度；边跨最大挠度出现的位置变化不大，说明中跨拱肋对边跨变形状态的影响较小。

从表3还可看出，随着刚度比的增加，中跨最大挠度和拱肋最大挠度出现的位置从跨中向四分点附近移动，表明结构从以梁为主的受力状态向拱桥状态转变；在刚度比增加到方案5（0．621 2）和方案6（1．438 8）之间的时候，结构受力逐渐转变为接近拱桥的状态。

由表4可知，拱梁刚度比较小时，结构一阶竖向振动模态为主梁正对称弯曲，拱梁刚度比较大时则为反对称弯曲。随着刚度比增加，主梁一阶正对称竖向振动频率略有增加，总体变化不大；一阶反对称竖向振动频率则明显减小。当结构拱梁刚度比超过方案3（0．143 1）之后，反对称模态开始先于正对称模态出现。当结构刚度比增加到某一程度时，一阶正对称竖向振动频率和反对称频率均稳定在某个值附近，说明此时竖向振动频率对竖向刚度比的敏感度较低。

6.2 构件内力分析

图4、图5 分别为计算得到的拱脚水平推力、主梁和拱肋控制截面内力与拱梁刚度比的关系，图6为二期恒载和活载作用下方案3和方案8结构的拱肋弯矩图。

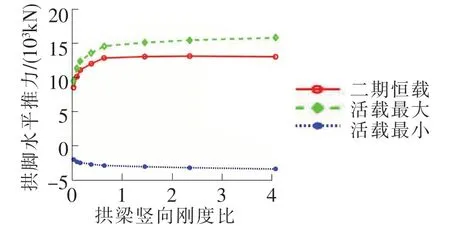
图4 二期恒载和活载作用下拱脚水平推力与拱梁竖向刚度比的关系

图5 二期恒载和活载作用下结构控制截面内力与拱梁竖向刚度比的关系

图6 二期恒载和活载作用下拱肋弯矩（包络）图（单位：kN·m）

由图4看出，二期恒载和ZK 活载作用下的最大拱脚推力随拱梁刚度比的增加而增加，拱肋在整个结构受力中占比越来越大；增大幅度明显由快变慢，当拱梁竖向刚度比达到0．621 2（方案5）后，拱脚水平推力趋于平稳。ZK 活载作用下的最小拱脚推力出现在活载集中布置在边跨时，拱肋由于主梁中支点附近产生的转角而受弯，进而对主梁产生压力；主梁抗弯刚度越低，中支点转角越明显，拱肋受弯作用越大。

分析图5可知，在二期恒载和ZK 活载作用下，中跨主梁的最大正负弯矩峰值随着刚度比增加而减小，而且减小的幅度较大，虽然拱肋分担荷载比增加不大，但拱肋对中跨主梁的辅助受力作用仍然非常明显。由于拱肋布置于中跨，拱肋刚度比增加的同时减小了边跨梁截面，二期恒载作用下边跨主梁的内力变化趋势与中跨相反。

从图6可看出，随着拱梁刚度比的增加，拱肋正弯矩区域范围扩大，最大正负弯矩绝对值均增加，负弯矩峰值向拱脚移动；刚度比较小时拱脚区域呈现正弯矩，刚度比较大时只有负弯矩。对于拱肋来说，拱肋嵌入主梁中，主梁中支点为拱肋提供约束条件；拱梁相对刚度较小时，中支点转动刚度较大，拱脚约束接近固结；拱梁相对刚度较大时，主梁对拱脚的转动约束较小，此时拱脚约束介于固结和铰接之间，相当于弹性约束。当拱肋刚度增加到1．0附近时，二期恒载作用下拱脚正弯矩消失，负弯矩峰值进一步向拱脚移动；刚度比增加到2．0以上时，活载在拱脚附近产生的最大负弯矩超过正弯矩。

拱脚插入主梁的构造形式为拱肋提供了边界约束条件，同时也使得该节点处拱梁相互影响，共同受力。当主梁刚度远大于拱肋刚度时，二期恒载作用下拱梁结合段变形不大，此时拱肋上的吊杆拉力传递到拱脚时不能产生较大转角，结合段对拱脚的约束作用类似于固定端，拱脚存在正弯矩区段。随着拱梁刚度比增大，当结合段对拱脚施加的边界条件接近固定铰约束时，正弯矩区段消失，拱脚正负弯矩幅值极小。拱梁刚度比增加过程中，主梁对拱脚的约束作用越发减弱，拱梁结合段的转角变形将更多地受到边跨主梁的影响，因二期恒载作用下的边跨主梁挠曲较大，但中跨主梁由于受到拱肋的辅助受力作用而变形不大，此时主梁对拱肋的影响相当于带有强制位移（转角）的固定铰约束。

6.3 拱肋分担荷载比

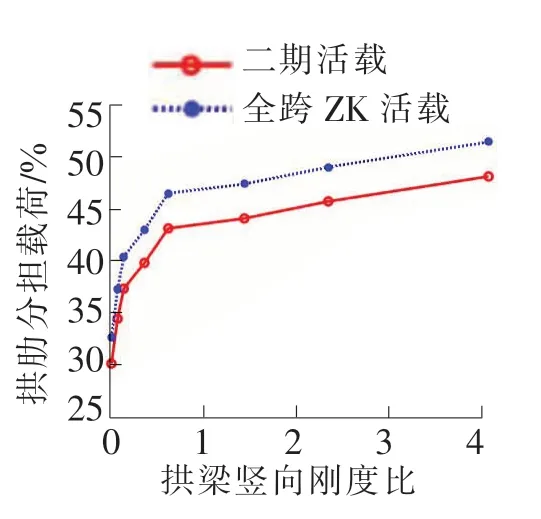
图7 二期恒载和活载作用下拱肋分担荷载比与拱梁竖向刚度比的关系

图7为拱肋承担荷载比与拱梁刚度比的关系。从图7可看出，即使是拱梁刚度比较小的结构（如方案1，拱梁刚度比0．010 2），拱肋分担荷载比例也达到了30%以上，说明拱结构对梁的承载能力和变形能力具有良好的辅助作用，充分体现了梁-拱组合结构的受力特征。随着拱梁刚度比的增加，拱肋承担荷载比例也逐渐提高，但由于在梁高较低时，边中跨径比0．5的连续梁也具有一定的承载力，而且如6．2节所述，边跨主梁在中支点附近的转角会降低拱肋承担载荷的能力，因此拱肋承担荷载并不能达到很高的水平。