新型履带式管道机器人变径机构动力学分析与仿真
2019-12-17张保真王战中杨晨霞
张保真, 王战中, 杨晨霞
(石家庄铁道大学 机械工程学院,河北 石家庄 050043)
近几十年来,随着我国科技的进步,工业的发展和经济水平的提高,我国管道运输建设取得了巨大的成果。到目前,中国建成油气管道总里程已超过13万km,建成初具规模的跨国、跨区域油气管网,中国管道工业的发展速度和技术水平跨入世界先进行列,仅就中国石油来说,年均建设管道里程在8 000 km以上[1]。油气输送管道腐蚀、穿孔或者破裂,都会造成油气泄漏,进而影响周围环境,甚至发生火灾、爆炸等严重后果。目前国内油气输送管线大部分为埋地敷设,埋深均在冻土层以下,发生腐蚀、裂缝等事故时,不易被发现。油气输送管道某处发生事故以后,就必须全线停止输送,进行抢修。如果停输时间较长,输油管道又可能造成凝管事故,并会产生巨大的经济损失。油气输送管线多在野外,在跨越河流、穿越农田时出现穿孔会造成严重环境污染和经济损失,严重时可能导致火灾、爆炸等事故,破坏油气输送设施的正常运行。为了保障人民的生命财产安全,社会环境的安定和自然环境不受到破坏,定期对油气输送管道进行检测是十分必要的。管道机器人作为有效的检测设备,可以代替人类执行检测任务[2]。研究并设计具有实际工程化应用价值的管道机器人,能够极大地提高管内检测和管内作业的准确性和可靠性,提高工作效率,使得人们可以对各类管线采用非挖掘和拆分的方式来进行探测及修复。美国GE 公司、瑞士ROSEN 公司等生产了流体驱动式管道机器人PIG[3],利用机器人两端的管道内流体压力差来提供动力,结构简单,使用性好。美国卡内基梅隆大学和美国国家能源部共同研发了Explorer系列模块化轮式燃气管道检测机器人,其采用视觉和漏磁双重检测手段[4]。邓宗全等[5]针对海底管道研发出六轮驱动的轮式管道机器人。张云伟等[6]设计了一种基于丝杠螺母传动,平行四边形轮腿支撑漏磁管道检测机器人。
为了使管道机器人适应复杂的管道环境,要求管道机器人具有变径机构。目前,国内外支撑轮式管道机器人常用变径机构主要包括:弹簧变径机构,蜗轮蜗杆变径机构,升降机变径机构及丝杠螺母副变径机构[7-8]。基于升降机式与滚珠丝杠螺母副式变径机构,提出了一种滚珠丝杠螺母副三角升降式变径机构,在分析其工作原理和变径过程中力学特性的基础上,建立优化数学模型,并基于多体动力学仿真软件ADAMS对其结构参数进行优化。
1 管道机器人变径机构工作原理与力学分析
1.1 变径机构工作原理
管道机器人的变径机构在变径过程中既要能顺利通过障碍,又要保证其驱动轮对内管壁有足够的压力来提供驱动力。管道机器人的模型如图1所示,其主要由履带足和变径机构组成。履带足通过直流空心杯电机,通过齿轮传动,驱动履带轮带动履带控制管道机器人行进和转弯。本文所描述的变径机构由升降机式变径机构和丝杠螺母式变径机构组合创新而来,整个变径机构主要有步进电机、传动齿轮与双旋向滚珠丝杠副组成的主动调节机构和弹簧组等组成的被动调节机构两部分。主动调节机构和被动调节机构最终都需通过调节3组沿管道机器人轴线间隔120°均布的支撑杆系来控制管道机器人径向大小的变化。滚珠丝杠副沿管道机器人中心轴线布置,同步盘在导向杆的约束下与滚珠丝杠螺母固连。步进电机驱动滚珠丝杠旋转,带动滚珠丝杠螺母及与其固连的同步盘沿导向杆向前、向后滑动。铰接在同步盘上的3组支撑杆系随同步盘做运动,使支撑杆系张开或者收缩以适应管径的变化。被动调节机构可以在不驱动主动调节机构的情况下帮助机器人顺利通过较小的障碍,并辅助实现驱动轮紧压在管壁上。压力传感器通过检测弹簧组预紧力,间接实现变径机构压力信号检测,检测到的压力信号作为反馈信号实现变径机构闭环控制。
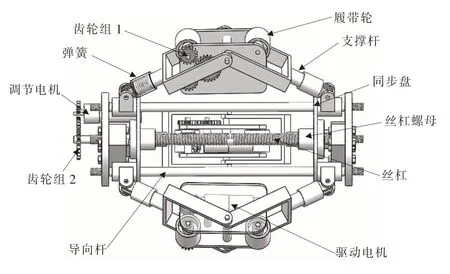
图1 管道机器人模型
1.2 变径机构动力学分析
取变径机构中的一组支撑杆系进行研究,其受力结构简图如图2所示。A、B 两点是铰接在同步盘上的两点,同步盘固连在丝杠螺母上,点B 是杆AB 和杆CB 的铰接点。R1和R2分别是杆AB 和杆CB 的长度,R3是点A 和点C 之间的距离。角γ和角β 是支撑角。
在图2所示坐标系下,建立机构的力封闭矢量方程
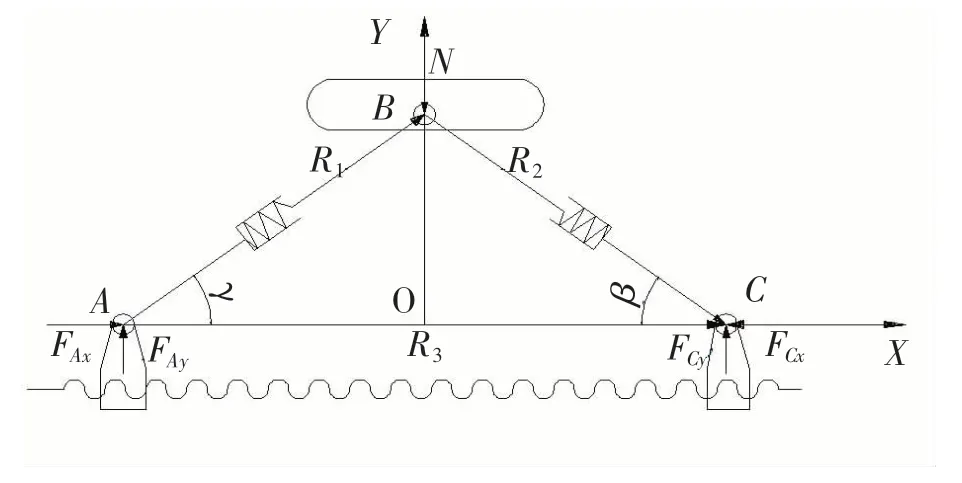
图2 变径机构一组支撑杆系受力简图

将矢量方程(1)投影到x 轴和y 轴上有

由几何关系得

对式(2)求一次导得

式中,ω 为杆AB 和杆CB 的角速度;˙R3为同步盘的线速度。
对式(4)求一次导得

式中,α为杆AB 和杆CB 的角加速度;¨R3为同步盘的线加速度。
铰接点A 的数值位移yA和螺母水平位移xB由式(6)确定

对式(6)求导,得铰接点A 和同步盘以支撑杆角度θ 为自变量的瞬时速度分量

基于虚功原理丝杠螺母变径机构在外力作用下做功之和为零可得

式中,N 为管道机器人在垂直管道攀爬时履带足对铰接点A 的正压力。
同步盘固连在丝杠螺母上,同步盘位移可用丝杠螺母位移表示,独立考虑丝杠螺母,螺母位移可表述为

式中,Ph为螺母导程;Ψ 为丝杠与螺母的相对转角。
在式(9)的基础上,基于虚位移原理,丝杠螺母传动机构在瞬时小位移条件下存在下述平衡关系

式中,T 为驱动电机瞬时输出转矩;η为丝杠螺母传动效率。
忽略铰接处等能量的损失,综合式(6)~式(10),三角形丝杠螺母—支撑杆变径结构电机输出转矩为

2 变径机构的优化模型建立
2.1 设计变量
由式(3)可知支撑杆长R1、R2可用l表示,支撑角γ 和β 可用θ 表示。分析式(6)~式(11)可知管道机器人在变径过程中影响调节电机驱动转矩大小的因素有R1、R2、γ和β。式(11)可知角度θ可以直接影响电机输出转矩的大小,所以优化向量可确定为:x={θ}。
2.2 目标函数
在保证可以正常工作并有足够的工作余量的情况下,要求驱动电机驱动转矩最小,且驱动效率最高。由图2可知,本文设计的新型变径机构螺母转矩可以直接反映电机转矩的大小,所以确定需要优化的目标函数为:f(X)=min(T螺母)。
2.3 约束条件
根据变径机构的几何关系,变径范围340~450 mm 以及结构紧凑性的要求,可以确定同步盘的行程S 以及支撑杆长的约束条件:其中,S 为同步盘的行程;H1为管道机器人中心轴线到铰点O 或B 的距离;H2为铰点C 到履带面的距离;l为杆长R1和R2;θ为支撑角γ 和β。
为满足支撑杆刚性以及电机转矩的要求,支撑角γ 和β可以约束为:20°≤θ≤70°。
3 动力学优化仿真
3.1 创建仿真模型
为使后续参数化建模优化设计方便,本次采用参数化建模。使用设计变量进行参数化建模时,通过改变设计变量,与设计变量相关的对象都得以自动修改,并通过分析设计变量对目标函数的影响,得到目标最优时的设计变量。利用ADAMS对变径机构进行参数建模和动力学优化仿真流程如图3所示。
选取变径机构的一组撑杆机构进行建模和动力学仿真。本文主要研究变径机构在最大支撑力N 的情况下,选择符合驱动转矩要求的驱动电机与合适的支撑角变化范围。支撑杆系中弹簧预紧力是变径机构中的内力,弹簧力的变化造成支撑力的变大或变小,但都比本次研究所使用的支撑力N小,所以弹簧对变径机构造成的影响可以忽略。
在ADAMS/View 软件中利用Design Exploration/Design Variable创建如表1所示的仿真过程中所需要的设计常量与变量,并创建O、A、B、C、D、E 6个设计关键点。以表1设计变量/常量为基本元素将创建的设计关键点坐标按表2对应关系式进行参数化表达。在ADAMS/View 中,以设计关键点为基础创建支撑杆系。此外,还需要添加约束,在支撑杆AB 与支撑杆BC、支撑杆AB 与螺母1、支撑杆BC 与螺母2铰接处添加转动副,在螺母与丝杠间添加螺旋副,螺母与大地间添加移动副。在支撑杆与履带足铰接的铰点上施加一大小为90 N 方向垂直滚珠丝杠的力,等效支撑力N,为简化模型履带足与支撑杆上的弹簧均未建立,另将所有部件视为刚性元件,忽略各铰接点的摩擦力。在ADAMS/View 中建立的模型如图4所示。

图3 动力学仿真流程图

表1 设计变量/常量

表2 设计关键点参数化坐标 mm
3.2 动力学仿真试验与结果分析
在支撑角20°≤θ≤70°和支撑力N 的约束下,支撑角A 与螺母位移S 及转矩T 的关系如图5所示。图5显示仿真的初始支撑角为45°,螺母位置在113 mm 处,支撑角A 与螺母位移S 及转矩T 都呈周期性变化。在一个周期内,支撑杆的支撑角随螺母沿丝杆轴向位移的减小而增大,增大而减小。驱动螺母的转矩则是先减小再增大再减小,最后再经过2个较小的波动。
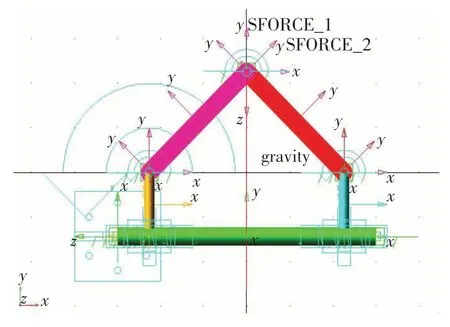
图4 变径机构动力学仿真模型
图6是支撑杆的支撑角在20°~70°变化时,对应支撑角与驱动螺母转矩的变化关系。支撑角在20°~53°时,与驱动螺母转矩呈抛物线型关系,在53°~70°呈正比例关系,随角度的增大而增大。图7是螺母位移与驱动螺母转矩变化关系,螺母位移在65~103 mm 时,驱动螺母转矩随螺母位移增大而减小,在103~155 mm 是先增大再减小。当螺母位移为88~122 mm时,驱动转矩较小,为0~2.5 N·mm,对应的管道机器人变径范围为362~421 mm,此变径范围是所需驱动转矩较小时对应的较优变径范围。
由图8可知支撑角与螺母位移呈近似的反比线性关系,在螺母位移为65 mm 时支撑角最大为70°,螺母位移为155 mm 时支撑角最小为20°。结合图6、图7与图8分析,可以知道当支撑角在43°~60°,螺母位移在88~122 mm 范围时,为较优选择范围,此时管道机器人变径范围为362~421 mm。考虑到管道机器人既要满足Ф340 mm~Ф450 mm 的变径范围,又可以顺利的通过弯曲管道,初选择支撑角的变化范围为30°~65°,在支撑杆长等仿真参数确定的条件下,螺母驱动转矩与螺母位移及支撑角变化的关系可以为后续选择驱动滚珠丝杠电机转矩与支撑杆的支撑角度的变化范围提供方便。

图5 支撑角、螺母位移及驱动螺母转矩仿真关系曲线
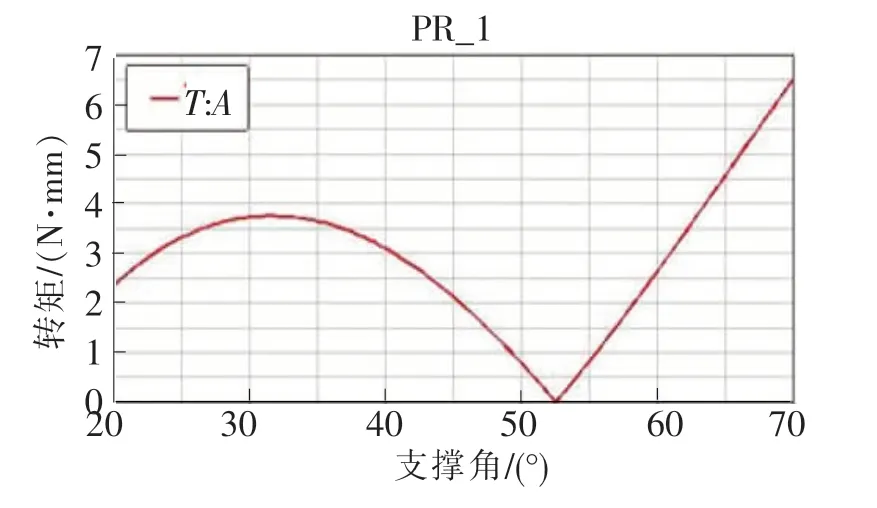
图6 支撑角与驱动螺母转矩仿真关系曲线
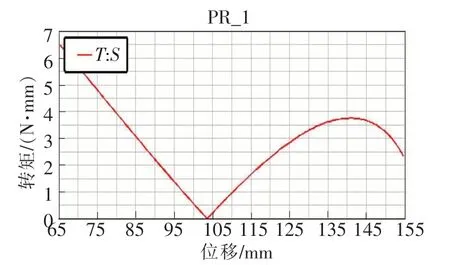
图7 螺母位移与驱动螺母转矩仿真关系曲线

图8 螺母位移与支撑角仿真关系曲线
4 结语
(1)提出了一种基于升降机式变径机构与丝杠螺母副变径机构的半菱形丝杠螺母副变径机构,并介绍了其工作原理。
(2)新型变径机构的驱动电机转矩较小,且具有更高的驱动效率和更好的管道适应性。
(3)通过对新型变径机构的力学分析和基于ASAMS的动力学仿真分析,了解驱动螺母转矩随支撑杆支撑角度及螺母位移的变化关系,可以选择更好的支撑角变化范围与螺母的移动范围,有助于驱动电机对支撑角更好地控制,同时为管道机器人整体设计及零部件的选择提供了方便。
(4)通过对变径机构的动力学仿真分析,可知在较优驱动转矩范围0~2.5 N·mm 时,支撑角的变化范围为43°~60°,对应管道机器人较优的变径范围是362~421 mm。
