不同强度理论在曲轴疲劳研究中的对比应用

2019-12-17孙嵩松万茂松徐晓美

中国机械工程 2019年23期

孙嵩松万茂松徐晓美张营

南京林业大学汽车与交通工程学院，南京，210037

0 引言

在实际工作过程中，曲轴等发动机零部件会受到不同激励源的周期性非比例载荷的作用，一些关键部位如圆角、油孔等由于截面形状的突变，会产生应力集中现象，并最终导致零部件的疲劳破坏，同时制造工艺、表面处理工艺等因素也会对零部件的疲劳特性产生间接影响[1-2]，因此如何准确预测零部件的疲劳特性，对零部件的生产设计有着重要的指导意义[3]。

针对上述问题，研究人员提出了相应的研究方法，其中临界距离法被认为是能够有效预测构件疲劳极限载荷的方法之一[4]。该方法最先由Neuber等提出[5]，而后TAYLOR[5-6]基于断裂力学的相关理论，提出了临界距离的新定义方法，并基于此方法对一些缺口件及焊接件的疲劳特性进行了预测研究。还有学者基于相应的损伤参量提出了另一种临界距离的定义方法[7]。

目前国内已有不少关于曲轴疲劳方面的研究。戴杰涛等[8]将有限元分析与断口分析相结合，确定了曲轴疲劳断裂的主要原因是倒角半径过小，并提出了相应的改进方法；察博文等[9]采用数值仿真技术对曲轴经过中频淬火工艺处理后的残余应力进行了分析，并对其疲劳极限载荷进行了预测；崔广军[10]将有限元法和多体动力学相结合，对曲轴的疲劳特性进行了预测，取得了更为准确的预测结果；刘海燕等[11]将McDiarmid模型用于曲轴疲劳研究，结果表明，与Basquin等效应力模型相比，该模型能够更加准确地预测曲轴的高周疲劳寿命。

目前在实际工程中，临界距离法主要应用于预测一些结构较为简单的缺口件，关于曲轴这样结构较为复杂的零部件的应用较少。本文基于不同的强度理论及其相应的应力分布，结合有限元法对多款曲轴的疲劳极限载荷进行预测，并对预测结果进行了试验验证。

1 临界距离法的相关定义

最初的临界距离法认为，对于任意构件，其疲劳寿命不仅取决于应力最大点处的应力值，还与一定临界范围内的应力分布有关。临界距离法主要包括临界点法(PM)和临界线法(LM)。随后TAYLOR[5-6]依据断裂力学的相关理论，提出了一种临界距离的新定义方法，其表达式如下：

(1)

式中，L为构件的临界距离；ΔKth为构件材料的应力强度因子门槛值；σ为构件材料的疲劳强度(分为拉伸疲劳极限和剪切疲劳极限)。

在工程实际应用中，对于同种材料、同种工艺制成的构件，可认为二者的材质属性一致，因此当采用该种定义方法定义构件的临界距离时，其临界距离值可视作只与材料属性有关的常数，其中基于该定义的临界点法的等效应力可表示为

(2)

式中，σ(r)为构件破坏路径上某一点的应力值；r为该点距最大应力点的距离。

而基于该定义的临界线法的等效应力可表示为

(3)

对于同种材料制成的零部件，当它们的等效应力值一致时，其疲劳寿命也会一致。而对于曲轴这样结构较为复杂的零部件，当采用临界距离法对其疲劳特性进行分析时，主要存在如下两个问题：

(1)曲轴受到外载作用时，其应力分布状态通常较为复杂，很难用一个简单的分布函数确定，也无法直接对其进行在一定临界范围内的应力积分计算。

(2)曲轴为三维实体，当受到外载作用时，其应力最大处的应力状态往往不是单一的拉伸或剪切应力状态，很可能会呈现出一定的多轴应力应变特性[12]，因此无法采用单一的拉伸或剪切应力对曲轴的应力分布进行分析。

2 临界距离法的应用方法

2.1 应力分布拟合方法

针对上述不足，本文将有限元法和插值法相结合，对曲轴在弯矩载荷作用下的应力分布函数进行近似拟合。该方法的主要步骤如下：

(1)采用有限元法对曲轴在弯矩载荷作用下的应力状态进行分析，并记录曲轴破坏路径上各节点的应力值以及各节点与最大应力点之间的距离。

(2)以各节点与最大应力点之间的距离为自变量，以各节点自身的应力值为从变量，采用高次多项式插值法对应力分布进行拟合，并分别基于临界点法和临界线法获取相应的等效应力值。

2.2 强度理论选择

在实际工程应用中，主要应用的强度理论包括第一强度理论(最大主应力理论)，第二强度理论(最大线应变理论)，第三强度理论(最大剪切应力理论)以及第四强度理论(von Mises应力理论)。本文中，曲轴的材料为高强度合金钢，其疲劳类型属于高周疲劳。在实际工程中，该类疲劳问题通常均是基于应力-寿命疲劳模型进行研究。基于上述实际疲劳现象，选择第一、第三和第四强度理论及其相应的应力分布，并结合临界距离法对曲轴的疲劳极限载荷进行预测。

3 曲轴算例

3.1 基于第一强度理论的预测结果

基于第一强度理论(即最大主应力理论)，选择编号为N0的某款曲轴作为基准的研究对象，相应的有限元模型如图1所示。

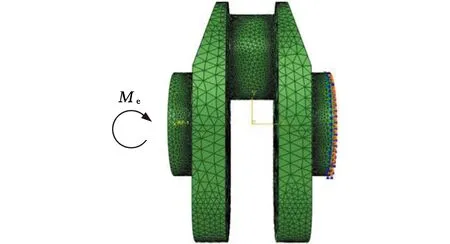
图1 曲轴有限元模型Fig.1 The finite element model of the crankshaft

根据圣维南原理，采用有限元法对曲轴在弯矩载荷作用下的应力状态进行分析时，其边界条件可简化为约束曲轴单拐主轴颈右截面的所有自由度，同时将弯矩载荷Me施加在单拐的左截面，其大小为曲轴的疲劳极限载荷值5 130 N·m，相应地，在该载荷作用下的最大主应力值为643 MPa，其位置位于曲轴的圆角处。

依据图2所示的曲轴疲劳失效过程中裂纹扩展的路径，记录最大应力点至曲轴内部一段距离内各节点的应力值，并利用裂纹模拟法获取在该应力分布下的应力强度因子门槛值[13]，拟合可得标准裂纹体的应力值及裂纹长度分别为312 MPa和2.02 mm。该标准裂纹体和曲轴二者之间的最大主应力分布的对比结果见图3。

图2 曲轴裂纹扩展路径Fig.2 Crankshaft crack propagation path

图3 裂纹模拟结果(基于第一强度理论)Fig.3 Crack-modeling result (based on the first strength criterion)

由图3可以看出，当基于第一强度理论(即最大主应力分布)时，利用裂纹模拟法所得到的标准裂纹体的最大主应力分布与曲轴自身的最大主应力分布基本一致。由断裂力学相关知识可知，在第一强度理论[13]下相应的标准裂纹体的应力强度因子门槛值ΔKth为24.86 MPa·m0.5。本研究中，N0曲轴的材料为高强度合金钢，其拉伸疲劳极限σb为501 MPa，代入式(1)计算可得基于第一强度理论的临界距离值

(4)

基于此参数和临界距离的相应定义，采用插值法对N0曲轴在其疲劳极限载荷作用下的应力分布进行拟合，可得在第一强度理论下N0曲轴相应的极限等效最大主应力值分别为

(5)

(6)

选择与N0曲轴圆角半径不同、材料属性一致的N1曲轴作为研究的对象，对其施加1 000 N·m的弯矩载荷，依照图2所示的路径纪录各节点的最大主应力值，相应的应力分布见表1。

表1 N1曲轴最大主应力分布(1 000 N·m载荷下)Tab.1 The maximum principal stress distribution ofcrankshaft N1(under 1 000 N·m loads)

由表1可知，N1曲轴在1 000 N·m的弯矩载荷作用下时，其圆角处最大主应力的最大值为234.2 MPa。利用已知的临界距离值求解N1曲轴在第一强度理论下相应的极限等效最大主应力值，则有

(7)

(8)

对比N1曲轴和N0曲轴的极限等效最大主应力值，可得N1曲轴在第一强度理论下，基于临界点法与临界线法的疲劳极限载荷预测值分别为

(9)

(10)

3.2 基于第三强度理论的预测结果

第三强度理论(即最大剪切应力理论)认为构件的疲劳寿命是由其最大剪切应力所决定的。基于此理论，记录N0曲轴在其疲劳极限载荷作用下的最大剪切应力分布，利用裂纹模拟法获取在该应力分布下的应力强度因子门槛值，拟合可得标准裂纹体的应力值及裂纹长度分别为9.6 MPa和665 mm。该标准裂纹体和曲轴二者之间的最大剪切应力分布的对比结果见图4。

图4 裂纹模拟结果(基于第三强度理论)Fig.4 Crack-modeling result (based on the third strength criterion)

由图4可以看出，当基于第三强度理论(即最大剪切应力分布)时，利用裂纹模拟法所得到的标准裂纹体的最大剪切应力分布与曲轴自身的最大剪切应力分布基本一致。由断裂力学相关知识可知，在第三强度理论[13]下相应的标准裂纹体的应力强度因子门槛值ΔKth为13.88 MPa·m0.5。同时本研究中N0曲轴材料的剪切疲劳极限τb为294 MPa，代入式(1)计算可得基于第三强度理论的临界距离值

(11)

基于此参数和临界距离的相应定义，采用插值法对N0曲轴在其疲劳极限载荷作用下的应力分布进行拟合，可得在第三强度理论下N0曲轴相应的极限等效最大剪切应力值分别为

(12)

(13)

同样对N1曲轴施加1 000 N·m的弯矩载荷，并记录该曲轴在该载荷作用下的最大剪切应力分布，结果见表2。

表2 N1曲轴最大剪切应力分布(1 000 N·m载荷下)Tab.2 The maximum shear stress distribution ofcrankshaft N1(under 1 000 N·m loads)

由表2可知，N1曲轴在该载荷作用下时，其圆角处最大剪切应力的最大值为118.5 MPa，利用已知的临界距离值求解N1曲轴在第三强度理论下相应的极限等效最大剪切应力值，则有

(14)

(15)

对比N1曲轴和N0曲轴的极限等效最大剪切应力值，可得N1曲轴在第三强度理论下，基于临界点法与临界线法的疲劳极限载荷预测值分别为

(16)

(17)

3.3 基于第四强度理论的预测结果

基于第四强度理论(即von Mises应力破坏理论)，利用裂纹模拟法获取N0曲轴在该应力分布下的应力强度因子门槛值，拟合可得标准裂纹体的应力值及裂纹长度分别为33.6 MPa和187 mm。该标准裂纹体和曲轴二者之间的von Mises应力分布的对比结果见图5。

图5 裂纹模拟结果(基于第四强度理论)Fig.5 Crack-modeling result (based on the fourth strength criterion)

由图5可以看出，当基于第四强度理论(即von Mises应力分布)时，利用裂纹模拟法所得到的标准裂纹体的von Mises应力分布与曲轴自身的von Mises应力分布基本一致。由断裂力学相关知识可知，在第四强度理论[13]下相应的标准裂纹体的应力强度因子门槛值ΔKth为25.8 MPa·m0.5，因此基于第四强度理论的临界距离值为

(18)

基于此参数和临界距离的相应定义，采用插值法对N0曲轴在其疲劳极限载荷作用下的应力分布进行拟合，可得在第四强度理论下N0曲轴相应的极限等效von Mises应力值分别为

(19)

(20)

同样对N1曲轴施加1 000 N·m的弯矩载荷，其von Mises应力分布见表3。由表3可知，N1曲轴在1 000 N·m的弯矩载荷作用下时，其圆角处von Mises应力的最大值为210.9 MPa。利用已知的临界距离值求解N1曲轴在第四理论下相应的极根等效应力值，则有

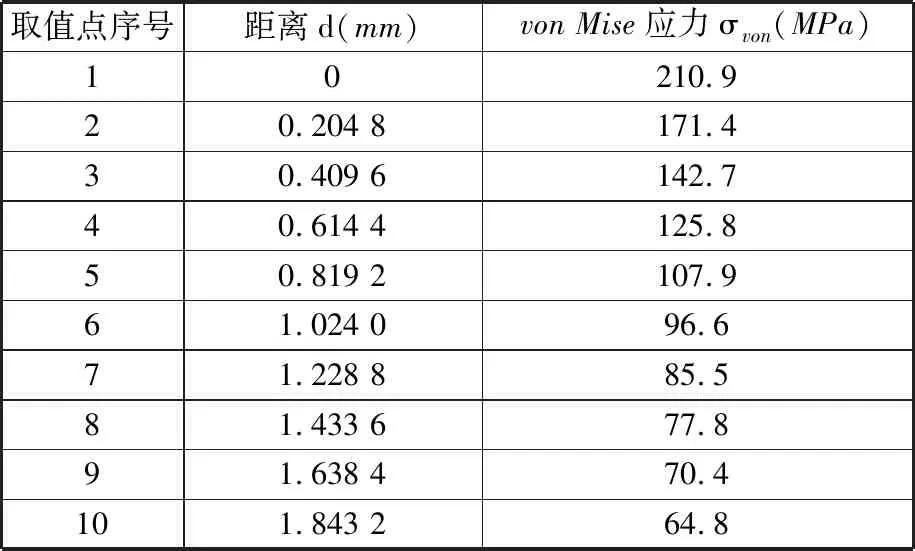
表3 N1曲轴von Mises应力分布(1 000 N·m载荷下)Tab.3 The von Mises stress distribution ofcrankshaft N1(under 1 000 N·m loads)

(21)

(22)

对比N1曲轴和N0曲轴的极限等效von Mises应力值，可得N1曲轴在第四强度理论下，基于临界点法与临界线法的疲劳极限载荷预测值分别为

(23)

(24)

4 试验验证及分析

由前文分析可以看出，基于临界距离法对零部件的疲劳极限载荷进行预测时，即使是同一款曲轴，当采用的强度理论不同时，其临界距离值和疲劳极限载荷的预测结果也有所不同。而且，即使是同一种强度理论，采用临界点法和临界线法的预测结果之间也存在较大的差异。为对该方法的适用性进行更加全面的评价，有必要对N1曲轴进行试验验证，相应的试验结果见表4。

表4 N1曲轴疲劳试验结果Tab.4 Fatigue test results of crankshaft N1

如表4所示，采用正态分布函数对该试验数据进行拟合[14]，可得N1曲轴疲劳极限载荷在50%失效概率下的中值为3 335 N·m，对比该数值及不同强度理论和临界距离法的预测结果，相应的误差见表5。

表5 N1曲轴的预测误差Tab.5 Prediction errors of crankshaft N1

由表5可知,当基于第一强度理论时，预测结果会导致误差较大(有时超过10%)；而基于第三和第四强度理论时，与临界点法相比，临界线法的预测精度更高(误差小于5%)，更适合用于曲轴的疲劳研究。

前期研究[15]中，笔者基于第三、第四这两种强度理论与临界距离法已对某款曲轴的疲劳特性进行了研究，预测结果的结论与本文一致。同时本文中基于第一强度理论的预测结果误差相对较大，笔者分析认为这是因为该强度理论认为构件的疲劳强度只与最大主应力有关，忽略了剪切应力对构件疲劳强度的影响。前期研究结果[16]表明，曲轴疲劳破坏的形式为剪切型破坏，这种差异导致了预测结果精度的不足。