用“等效替代法”破解初中物理难题

袁柏林

(四川省德阳中学校，四川 德阳 618000)

等效替代法是在保证某种效果相同的前提下,将实际的、复杂的物理问题和物理过程转化为等效的、简单的、易于研究的物理问题和物理过程来研究和处理的方法.

在初中物理教学中“等效替代”主要应用于实验探究之中,如:在浮力教学的“曹冲称象”案例中,用石头替代大象利用等效替代称出了大象的体重;在探究平面镜成像特点的实验中,用玻璃板等效替代平面镜、利用两个完全相同的蜡烛,其中一根等效另一根的像来探究物与像的大小关系;在探究合力与分力的关系、电路的总电阻与分电阻的关系、测量电阻等实验中都应用了“等效替代”思想.在实际教学过程中,特别是在竞赛辅导中,笔者通过长期研究发现:对于一些物理难题利用“等效替代”还可以使一些复杂的物理过程得到大大简化,甚至使一些用初中知识无法解答的问题得到破解.下面就列举几个应用实例加以说明.

1 利用力作用效果的等效性

力的作用效果包括静态效果(改变物体形状)和动态效果(改变物体的运动状态),动态效果又分为平动效果和转动效果.大小、方向、作用点、性质不同的力产生的效果可能相同.

1.1 用合力等效代替分力的作用效果

一个力的作用效果可能与几个力的作用效果相同,我们把这一个力叫那几个力的合力.若用合力的等效替代分力来分析研究,就可以使问题得到大大的简化.

图1

例1.两个半球壳拼成的球形容器内部已抽成真空,球形容器的半径为r,大气压强为p,为使两个半球壳沿图1中箭头方向分离,应施加的力F至少为

(A) 4πr2p. (B) 2πr2p.

图2

解析:由于大气压强是向各个方向的,压力的方向是垂直于受力物体表面,所以两个半球壳受到大气压力的方向如图2所示.由于大气对球面各个方向的压强都为p,球体的表面积S=4πr2,根据公式F=pS,若按常规思路,很容易错误的认为要把两个半球壳拉开,施加的力F至少应等于一个半球表面受到的大气压力,即F=2πr2p.

图3

而实际上,如图3所示,要把两个半球壳拉开,只需要克服半球所受大气各个方向压力的合力F′,我们用这个F′等效替代半球各个方向受到大气的压力,其方向与拉力F的方向相反,其受力面积等效于球的横截面积πr2.所以F=F′=pS=πr2p,故应选(C).

1.2 用分力等效代替合力的作用效果

大小、方向、作用点不同的两个力对杠杆的转动效果可能相同,用一个特殊的、便于分析的力等效替代另一个复杂的、变化的、不易研究的力,就可以变复杂为简单、变变量为恒量、变“无解”为“有解”．

图4

解析:要知道链条的节数,就应先求出链条的总重;要判断两木板距离增大时,AB板的旋转情况,就应分析当两木板距离增大时,链条作用在木板B端的力对AB板旋转的影响.然而作用在AB木板B端和CD木板D端力的大小和方向都不确定,仅利用初中知识,采用常规方法无法求解.那就让我们转换思路,采用等效替代法破解此问题.

图5

如图5所示,以长方形木板AB和CD为研究对象,铁链分别对B端和D端的拉力为FB和FD.FB的可以等效分解为FBx和FBy;FD的可以等效分解为FDx和FDy.其中FBx、FDx的方向分别过了杠杆支点O1、O2,其力臂为0,对杠杆AB和CD的转动没有作用效果.所以,FB和FBy、FD和FDy对杠杆的作用效果相同,可以分别用FBy和FDy等效替代FB和FD,这样杠杆的平衡就可以理解为是由木板受到的重力G和FBy(或FDy)决定的.根据杠杆平衡条件:G×O1O=FBy×O1B、G×O2O=FDy×O2D和已知条件:O为杠杆中点、AO1∶O1B=CO2∶O2D=2∶1，可得

(1)

图6

如图6所示,以铁链MN为研究对象,铁链在M端和N端受到的拉力为FM和FN,FM的可以等效分解为FMx和FMy;FN的可以等效分解为FNx和FNy,由平衡力和对称性知识可得

(2)

再根据相互作用力的特点可以得出

FMy=FBy.

(3)

FNy=FDy.

(4)

由(1)-(4)式可得G链=G.

2 利用力做功效果的等效性

在初中阶段,关于力做功问题一般只要求掌握力的大小不变,且力的方向与物体运动的方向一致的情况下,利用公式W=Fs来计算.但在一些初中物理竞赛和名校高中自主招生考试中常出现一些变力提升物体做功的问题,采用常规方法很难解答.但从力做功的效果来看,相当于把物体的重心提高一定的高度,此力所做的功与克服物体重力所做的功具有等效性，即W=Fs=Gh.

图7

例3.如图7所示,在力F的作用下要把一根长度为L,质量为m的均匀细圆柱体从水平放置竖立起来,若F的方向始终与圆柱体垂直,则在此过程中F至少要做多少功?

解析:如图7所示,在力F的作用下要把圆柱体从水平放置竖立起来,且F的方向始终与圆柱体垂直.说明圆柱体在提升过程中F的方向不断变化,但其力臂不变;重力的大小不变,其力臂逐渐变小.根据杠杆平衡条件可得F逐渐减小.若利用常规方法,直接利用W=Fs无法求解.

3 利用热传递效果的等效性

当温度不同的物体接触时,高温物体放出热量温度降低,低温物体吸收热量温度升高,直到温度相同,达到热平衡.若不计热损失,Q吸=Q放.把多个温度相同的物体先后逐个与另一个物体混合和把多个温度相同的物体同时一起与那个物体混合,在不计热损失的情况下,热传递的效果是相同的.但后者热传递的过程就简单多了.

例4.将一杯热水倒入盛有冷水的足够大的容器中,冷水的温度升高了10℃,再向容器内倒入一杯相同质量和温度的热水,容器中的水温又升高了6℃.如果继续向容器中一杯又一杯地倒入同样的热水,则倒入第13杯同样的热水时,容器中的水温会升高多少℃?(不计热损失)

解析:设原来冷水的质量为m1、初温为t01,一杯热水的质量为m2、初温为t02,第一杯热水与冷水混合后冷水的温度升高了Δt1;Q吸1=cm1Δt1,Q放1=cm2(t02-t01-Δt1).由于不计热损失:Q吸1=Q放1,即cm1Δt1=cm2(t02-t01-Δt1),又因为Δt1=10℃，所以

m1×10℃=m2(t02-t01-10℃).

(5)

若采用常规方法:设当倒入第二同样的热水混合后容器中的水温又升高了Δt2.

Q吸2=c(m1+m2)Δt2，

Q放2=cm2(t02-t01-Δt1-Δt2).

由Q吸2=Q放2,且Δt1=10℃,Δt2=6℃可以得

(m1+m2)×6℃=m2(t02-t01-16℃).

(6)

联解(5)、(6)式可得

t02-t01=40℃,m1=3m2.

设当倒入第三同样的热水混合后容器中的水温又升高了Δt3.

Q吸3=c(m1+2m2)Δt3，

Q放3=cm2(t02-t01-Δt1-Δt2-Δt3).

由Q吸3=Q放3,且t02-t01=40℃,m1=3m2，可以得Δt3=4℃.

利用同样的方法就可以逐一求每增加一杯热水,容器中的水升高的温度,至到计算出倒入第13杯同样的热水时,容器中的水升高的温度.此题虽然采用常规方法最终能得到答案,但此方法太繁琐,且倒水的次数越多,越不容易计算出结果.

若采用等效替代法:由于不计热损失,一杯一杯的热水先后倒入冷水中与把这几杯热水一起同时倒入冷水中效果相同.设把n杯热水一起同时倒入冷水中,容器中的水温升高ΔTn,那么,第n杯热水倒入后升高的温度Δtn=ΔTn-ΔTn-1.

一杯热水与冷水混合后,由Q吸1=Q放1，得

cm1×10℃=cm2(t02-t01-10℃).

(7)

两杯热水与冷水混合后,由Q吸2=Q放2，得

cm1×16℃=2cm2(t02-t01-16℃).

(8)

联解(7)、(8)式可得

t02-t01=40℃,m1=3m2.

12杯热水与冷水混合后,由Q吸12=Q放12得

cm1×ΔT12=12cm2(t02-t01-ΔT12).

(9)

将t02-t01=40℃,m1=3m2代入(9)式得

T12=32℃.

13杯热水与冷水混合后,由Q吸13=Q放13得

cm1×ΔT13=8cm2(t02-t01-ΔT13).

(10)

将t02-t01=40℃,m1=3m2代入(10)式得

ΔT13=32.5℃.

则倒入第13杯同样的热水时,容器中的水升高的温度:Δt13=ΔT13-ΔT12=0.5℃.

拓展:还可以推导出第n杯热水时容器中的水升高的温度的规律:

由cm1×ΔTn=ncm2(t02-t01-ΔTn)，

得3ΔTn=n(40℃-ΔTn).

4 利用电路、电阻的等效性

等效电路是指同一个电路的不同表示方法,元件的种类和位置都相同,但是在画电路图时有不同的画线方法;将一个电阻代替原来的几个电阻后,对整个电路的效果与原来几个电阻的效果相同,这一个电阻叫做那几个电阻的等效电阻(又叫总电阻).

图8

例5.把19个阻值均为r的电阻丝连接成如图8所示的图形,则AB间的总电阻为________r.

解析:要求电路的总电阻,就要先分析清楚其电路的连接情况,但图8不是简单的串联、并联或混联电路,利用初中知识、采用常规方法无法解答.

方法1:利用高中知识,电位相等的不同点之间即使用导线连通也没有电流,这些等电位的节点合成一个点不会影响电路效果,可称为等效电路.

图8中根据AB之间电路的对称性C、D两点的电位相等,E、F两点的电位相等,等效电路如图9.

图9

方法2:如图10所示,当两条相同电流通过一导体时,可以等效把此导体沿电流方向“切开”平分成两条电路,由于每一半的横截面积为原来的一半,所以其阻变为原来的2倍.这样既没有改变原来电路的等效阻值,又突破了解题的“瓶颈”,这样利用初中知识就可以解答此题了.

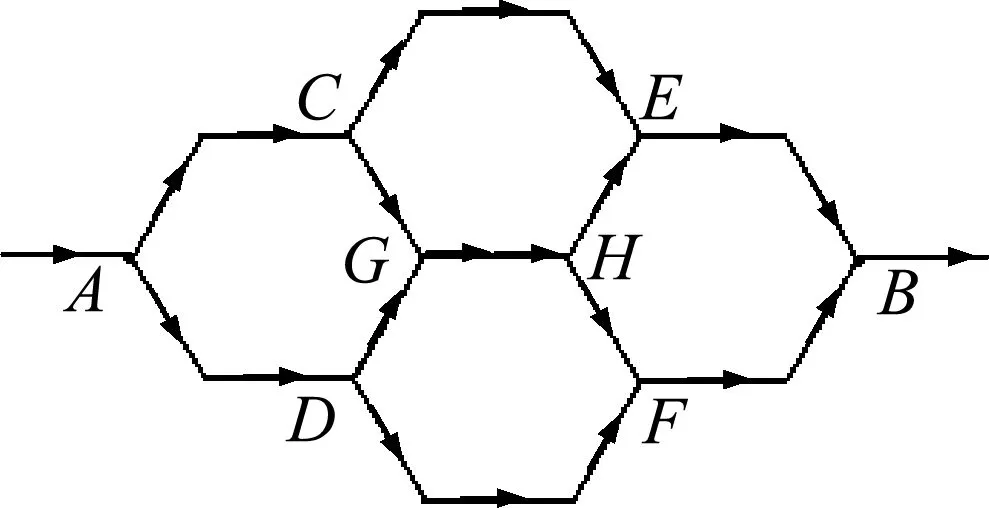
图11

图8的电流流向如图11所示,其中GH电阻丝上的“双箭头”表示有两条相同电流流过此电阻丝,可以等效成阻值为2r的两条电路,一条与CG、HE串联,另一条与DG、HF串联.

图12

综上所述,“等效替代法”是科学研究的重要方法.在初中物理教学中,除了在实验教学中有着广泛应用以外,在分析、解答一些物理难题上也能起到不可忽视的积极作用.恰当地利用等效替代法既可以使一些利用常规方法不易解答的难题得到破解,又能培养学生的科学思维能力,提高其理解、分析、推理以及思维的迁移和创新等能力,为学生进一步的学习乃至终身学习奠定基础.这正是素质教育的要求. 在提倡“核心素养”的今天,中考、高考、竞赛等选拔愈来愈注重考生的能力和素质,其命题愈加明显地渗透着物理思想、物理方法的考查,等效思想和方法作为一种迅速解决物理问题的有效手段,仍将在问题的突破过程中充分发挥其作用.