1种软轴推拉钢索运动关系的建模分析方法
2019-12-13郑伟连张让威
郑伟连,张让威
(中国航发沈阳发动机研究所,沈阳110015)
0 引言
在航空发动机结构设计中,运动关系的传递除齿轮传动、连杆传动和链条传动等结构形式外,软轴推拉钢索结构也得到了广泛应用。冯春玲等对软轴钢索的研制过程和关键技术开展了研究[1-3]。石晓龙对复材飞机操纵钢索的设计和应用进行了论述,总结性的提出了软式钢索操纵的设计步骤[4]。杨春宁等在利用等效动态模型法建立某型飞机机械式操纵系统完整的数学模型时,采用硬式传动机构的建模处理方法对软式钢索进行等效处理[5]。金忠庆[6-9]等开展了对钢丝绳传动机构的分析与实验研究。但是,目前对软轴推拉钢索运动传递关系尚未建立有效的数学模型,基于软轴推拉钢索的运动关系传递函数的设计还停留在试验仿真模拟阶段。
本文通过对软轴推拉钢索结构的简化,建立软轴推拉钢索运动关系传递模型。基于该模型对发动机中采用软轴推拉钢索实现运动关系传递的主燃油泵调节器和高压压气机静子可调叶片角度反馈机构进行了建模,得到运动关系传递函数并进行了优化设计,验证了本文方法的有效性。
1 软轴推拉钢索的建模
软轴推拉钢索结构由内心钢丝绳、复合外套、导向杆、螺母等组成,具体结构如图1所示。内芯钢丝绳在复合套管中的推拉运动传递运动关系,通过螺母将软轴推拉钢索两端固定在发动机外廓机匣上,导向杆可以绕螺母存在16°的偏转角。

图1 软轴推拉钢索结构
软轴推拉钢索在航空发动机运动关系的传递中具有以下优势:
(1)可靠性较高。软轴推拉钢索结构相对简单,能够满足航空发动机高可靠性的要求;
(2)体积小、质量轻。1根长度1700 mm的软轴推拉钢索质量不大于0.5 kg;
(3)能够适应发动机的复杂外廓。软轴推拉钢索柔性,能够满足发动机曲面弧形外廓的特点,占用空间小。
简化后的软轴推拉钢索如图2所示。软轴推拉钢索由状态1变成状态2,内芯钢丝绳在套管中相对两侧固定点运动。由于内芯钢丝绳和套管之间存在间隙,在往复拖动钢索时,拖动初期存在响应迟滞现象,即存在“空行程”ξ1。同时考虑内芯钢丝绳拉伸弹性,在拖动力的作用下弹性变形量为ξ2。将钢索的“空行程”和弹性变形引起的位移行程偏差统一定义为“空行程”:ξ=ξ1+ξ2。则内芯钢丝绳右端串动量L1和左端串动量L2满足:L1=L2+ξ。同时导向杆能够绕钢索固定点摆动,保证软轴推拉钢索能够传递角度运动关系。因此软轴推拉钢索运动传递关系模型为
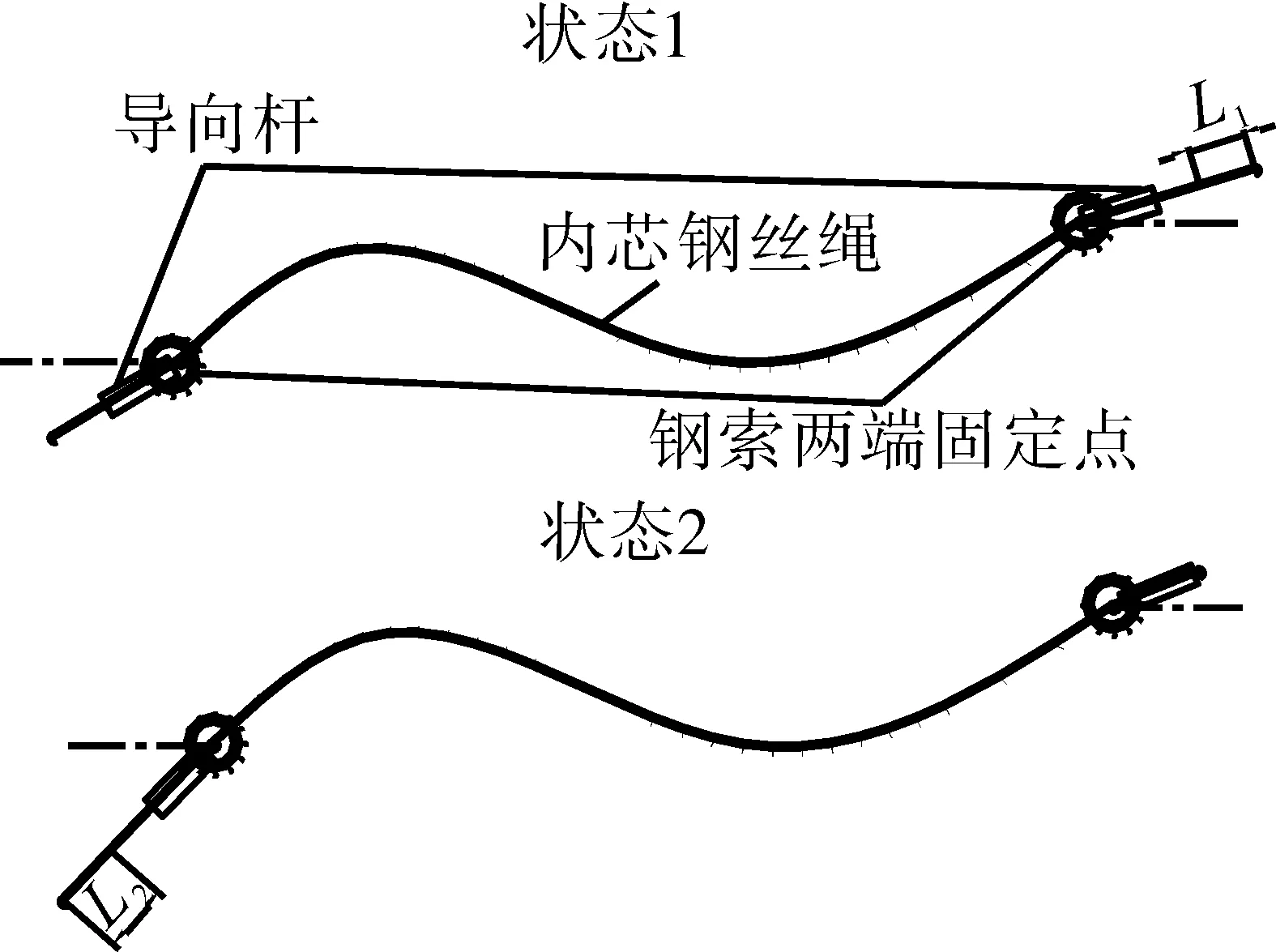
图2 软轴推拉钢索运动模型

式中:△L1和△L2均为钢索的位移绝对值。
2 软轴推拉钢索建模应用
在某型航空发动机中,主燃油泵调节器(以下简称主泵)将高压压气机静子可调叶片角度α2作为发动机控制的输入参数之一[10-12]。通过软轴推拉钢索及连杆机构实现主泵摇臂旋转角度和α2作动筒摇臂旋转角度关系的传递,将α2反馈给主泵。结构形式如图3、4所示,简化后的反馈调节机构如图5所示。
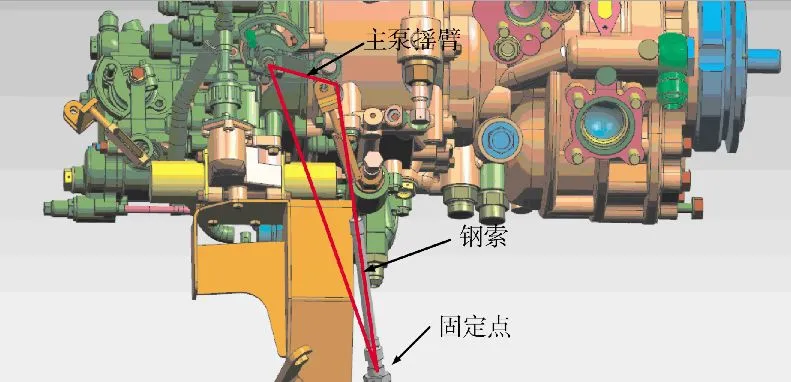
图3 主燃油泵控制器摇臂结构
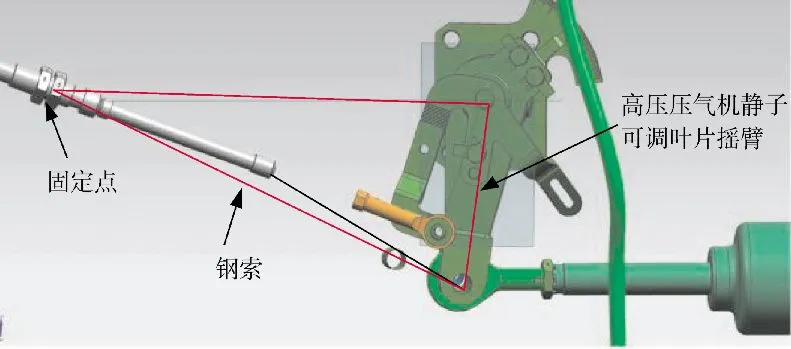
图4 α2作动筒摇臂结构
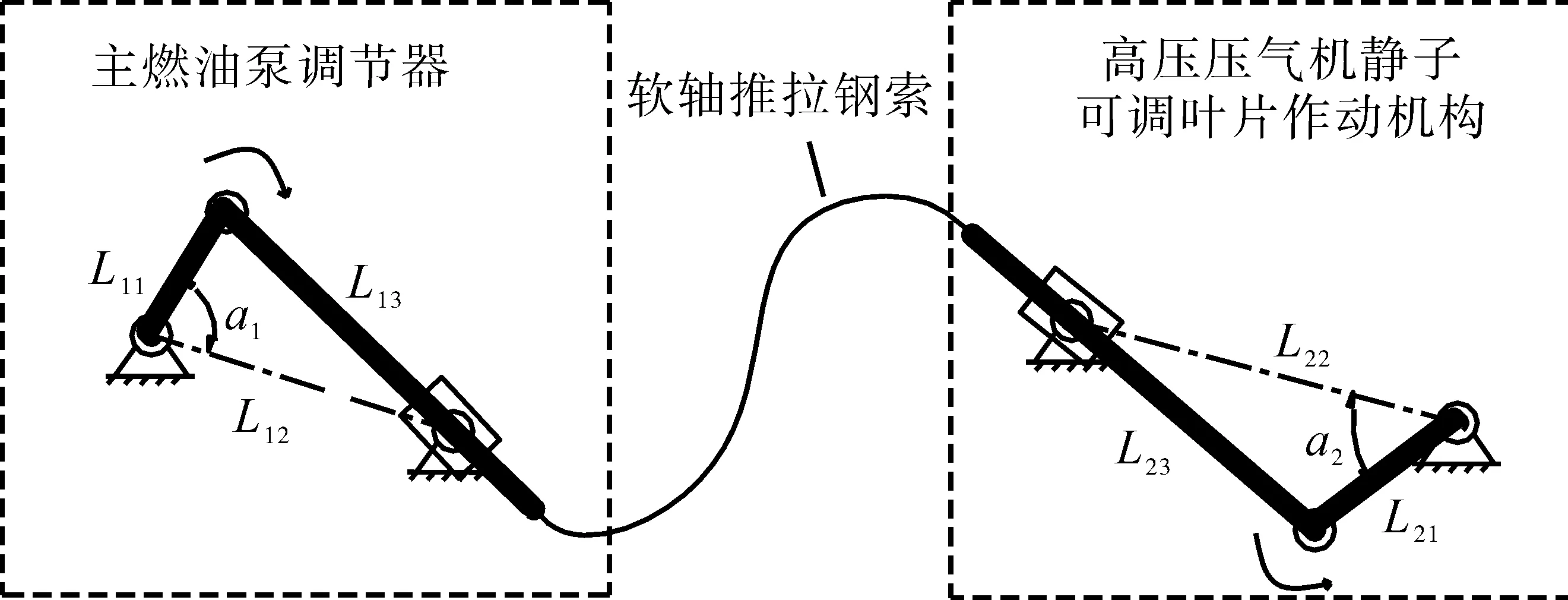
图5 简化后的a2角位移反馈机构
在图 5 中:L11=40 mm,L12=210 mm,a1的初始角度为 60°(可调),转动角度范围为 30°;L22=190 mm,a2的初始角度为50°,转动角度范围为45°。在反馈机构安装过程中,通过调节L21的长度保证a1和a2的角度范围关系相互协调,即当 a1=60°时,a2=50°;当 a1转动30°后,a1=60°-30°=30°时,a2=50°+45°=95°。
设主泵摇臂摆动角度为 y,0<y<30°,则摇臂摆动过程中L13的伸长量为

△L13随主泵摇臂转动的变化曲线如图6所示。
从图中可见,△L13单调增加,求出最大的△L13Max=16.64 mm。依据软轴推拉钢索运动关系的传递特点:△L13=△L23+ξ,求出此时L23的长度
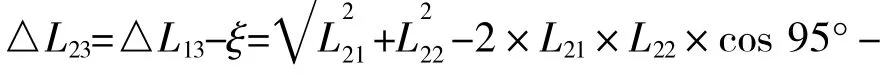
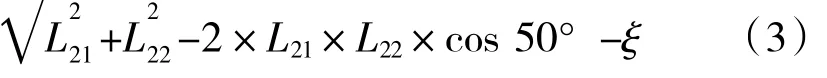
该型软轴推拉钢索的产品说明书中描述其“空行程”不大于1 mm,本文取“空行程”ξ=1mm 。求得 L21=20.87 mm。
为了使L11的转动范围(0~30°)和L21的转动范围(0~45°)一致,主泵摇臂初始角度α1和α2作动机构摇臂长度L21之间的关系曲线如图7所示,并应满足
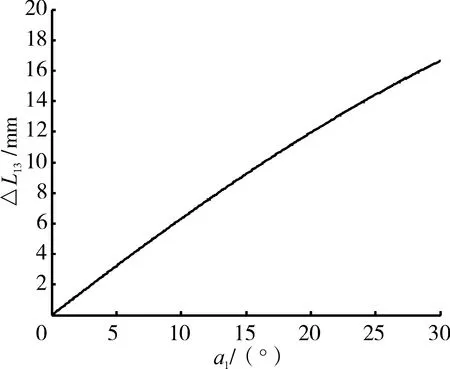
图6 △L13随主泵摇臂转动的变化曲线
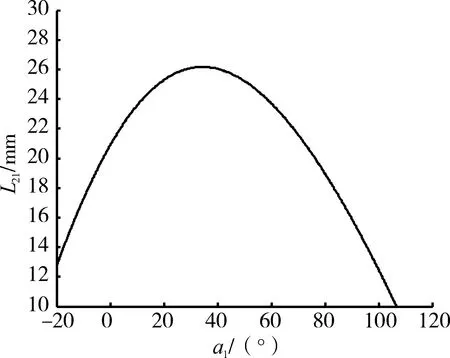
图7 a1和L21约束关系曲线
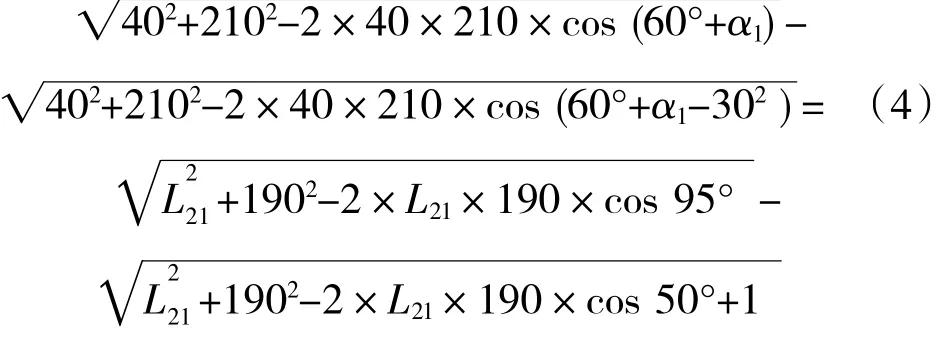
从图中曲线可以得出:在满足摇臂摆动角度行程协调的情况下,α2作动筒摇臂的长度存在1个极大值。
主泵摇臂和α2作动筒摇臂角度关系的传递通过软轴推拉钢索实现。基于第1章的建模,得到钢索两端的移动量分别为

当正向拖动钢索时(正行程),满足

当反向拖动钢索时(反行程),满足

当忽略钢索空行程时,满足

主泵摇臂角度α1和α2作动筒摇臂角度α2运动关系曲线如图8所示。
由于“空行程”的存在,导致“理论曲线”发生平行偏移,即主泵摇臂角度α1和α2作动筒摇臂角度α2对应关系点在2条“曲线带”内。
将发动机理论计算得到的α1和α2关系曲线和发动机实际装配过程中排除“空行程”后测得的a1和a2关系数据点进行对比,结果见表1,并如图9所示。从图中可见,理论计算关系曲线和实际测量结果接近,偏差小于3%,证明了建模方法的合理性和建模结果的有效性。
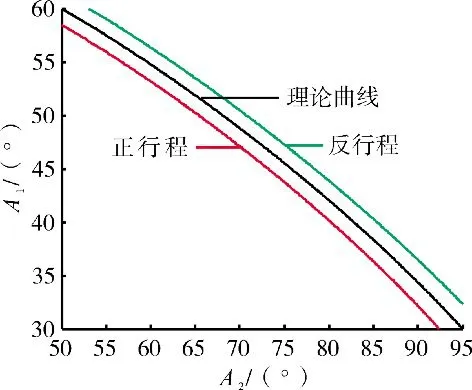
图8 a1和a2理论关系曲线
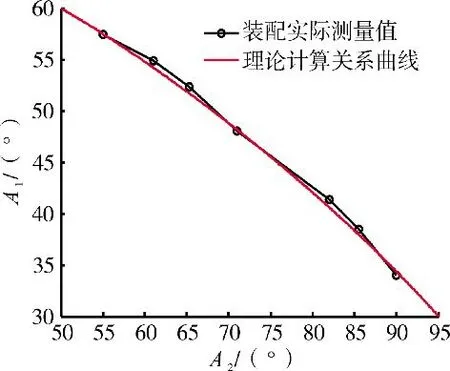
图9 a1和a2理论关系曲线和实测值对比
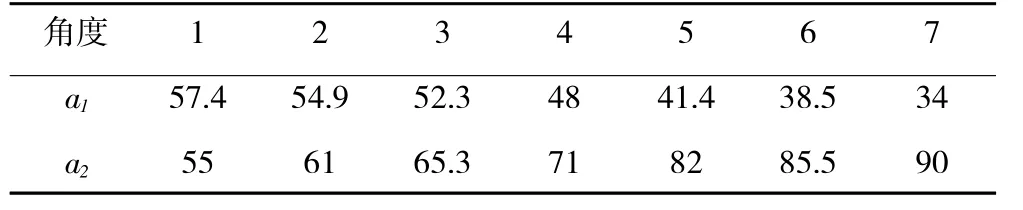
表1 a1和a2关系实测数据 (°)
3 关系曲线的优化设计
第2章中得到的a1的a2理论关系曲线为1个非线性的函数关系。在工程实际中,为了对发动机的控制规律进行现场掌握和调节,需要根据主泵摇臂角度a1的读数计算a2角度。由于a1的a2理论关系曲线的非线性给计算带来了困难,发动机试车人员通过现场作图描点的方法确定a1的a2对应关系,存在准确性差、效率低的问题。
为了降低发动机试车现场试车人员的工作难度,有必要对a1和a2的理论关系曲线进行优化,得到近似线性形式的关系曲线函数。
定义理想的1阶线性函数为

式中:a、b为线性函数系数。
由于a1和a2角度关系分别满足其角度行程范围,即当 a1=60°时,a2=50°;当 a1=30°时,a2=95°。即理想线性函数通过点(50,60)和点(95,30)。因此得到理想线性函数
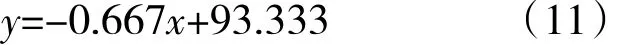
通过对a1初始角度和L21进行优化,得到最优的a1和L21组合,使得a1和a2的关系曲线近似于式(11)的直线形式。
同时还必须保证a1和a2的转动范围协调一致,即需要满足式(4)规定的a1和L21约束关系。
理论关系曲线的隐函数表达式为
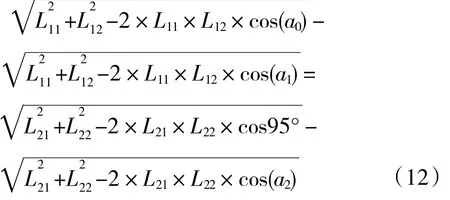
式中:a0为a1的初始角度。
a0和L21为优化变量。由于“空行程”仅会引起a1和a2关系曲线平移,不影响其线型,此处未考虑“空行程”对关系曲线的影响。
定义优化目标函数为

式中:y1为a1和a2理论关系曲线隐函数(式(12));y2为理想线性函数(式(11))。
为使得优化曲线y1和理想线性曲线y2更加“贴合”,定义优化目标为阴影部分的面积最小,如图10所示。即求出最优的主泵摇臂的初始角度a0和a2作动筒摇臂长度L21使得a1和a2理论关系趋近如式(11)所示的直线形式。
同时优化变量a0和L21还必须满足如下约束关系
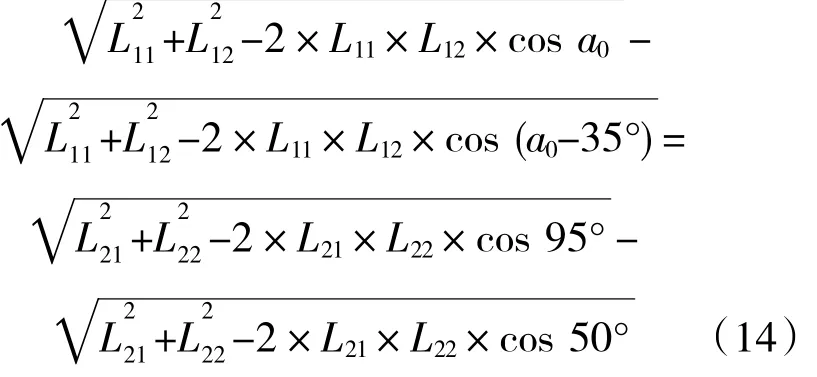
以上优化问题为1个包含约束的非线性优化问题。
共轭梯度法是介于最速下降法与牛顿法之间的1个方法,克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,是解决非线性最优化问题最有效的算法之一[13-15]。采用共轭梯度法对以上问题进行优化计算,得出优化结果为:a0=62.3°,L21=22.88 mm。a1和 a2理论关系曲线优化前、后的结果对比如图11所示。在发动机总装安装推拉反馈钢索时,保证主泵摇臂初始角a0=62.3°,α2作动筒摇臂长度L21=22.88 mm,测量a1和a2关系数据实测值。将实际测量结果和式(11)的理想线性函数进行对比,如图12所示。实际测量结果和理想线性函数的误差小于1%,达到了优化的目标。
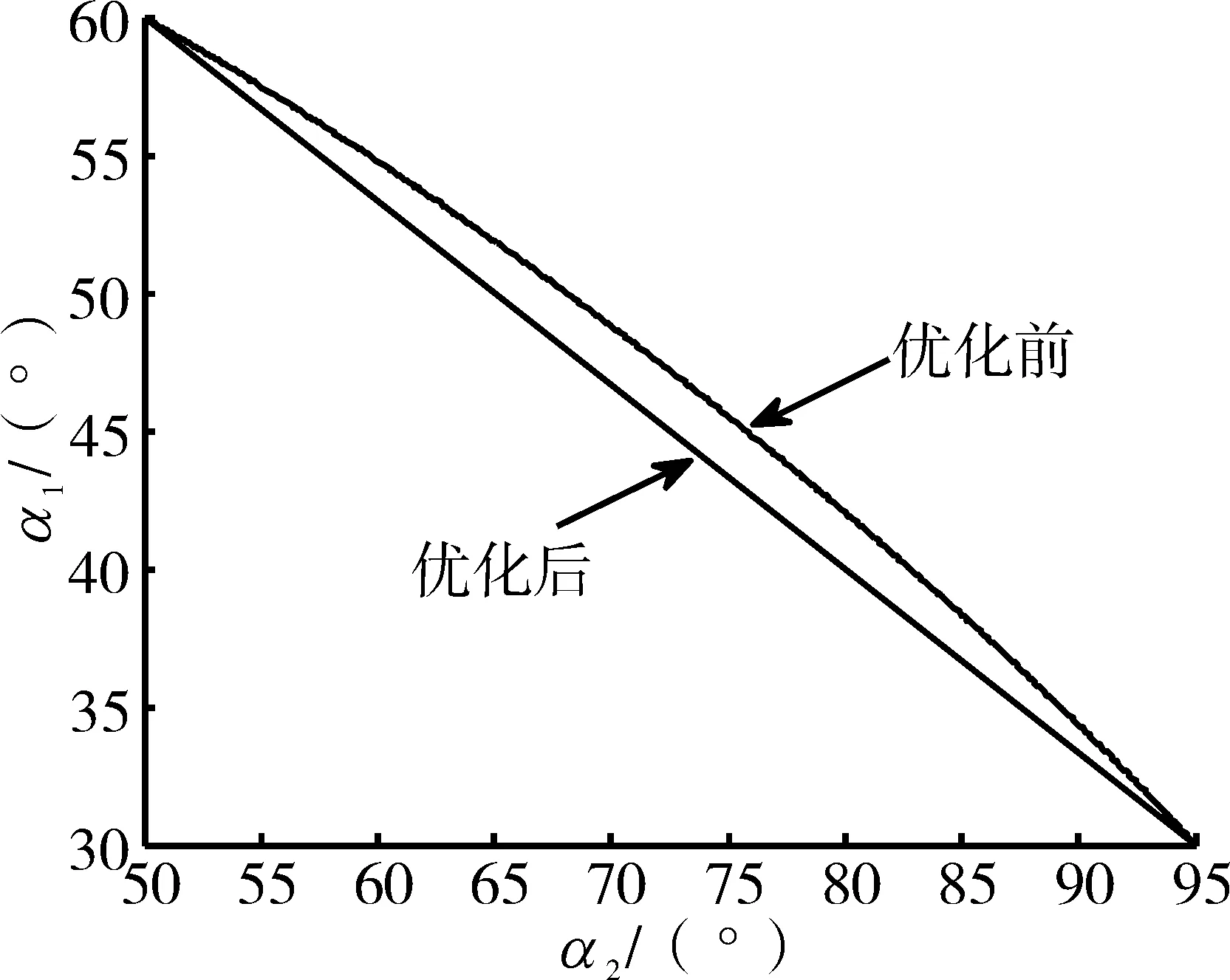
图11 优化后的a1和a2理论关系曲线
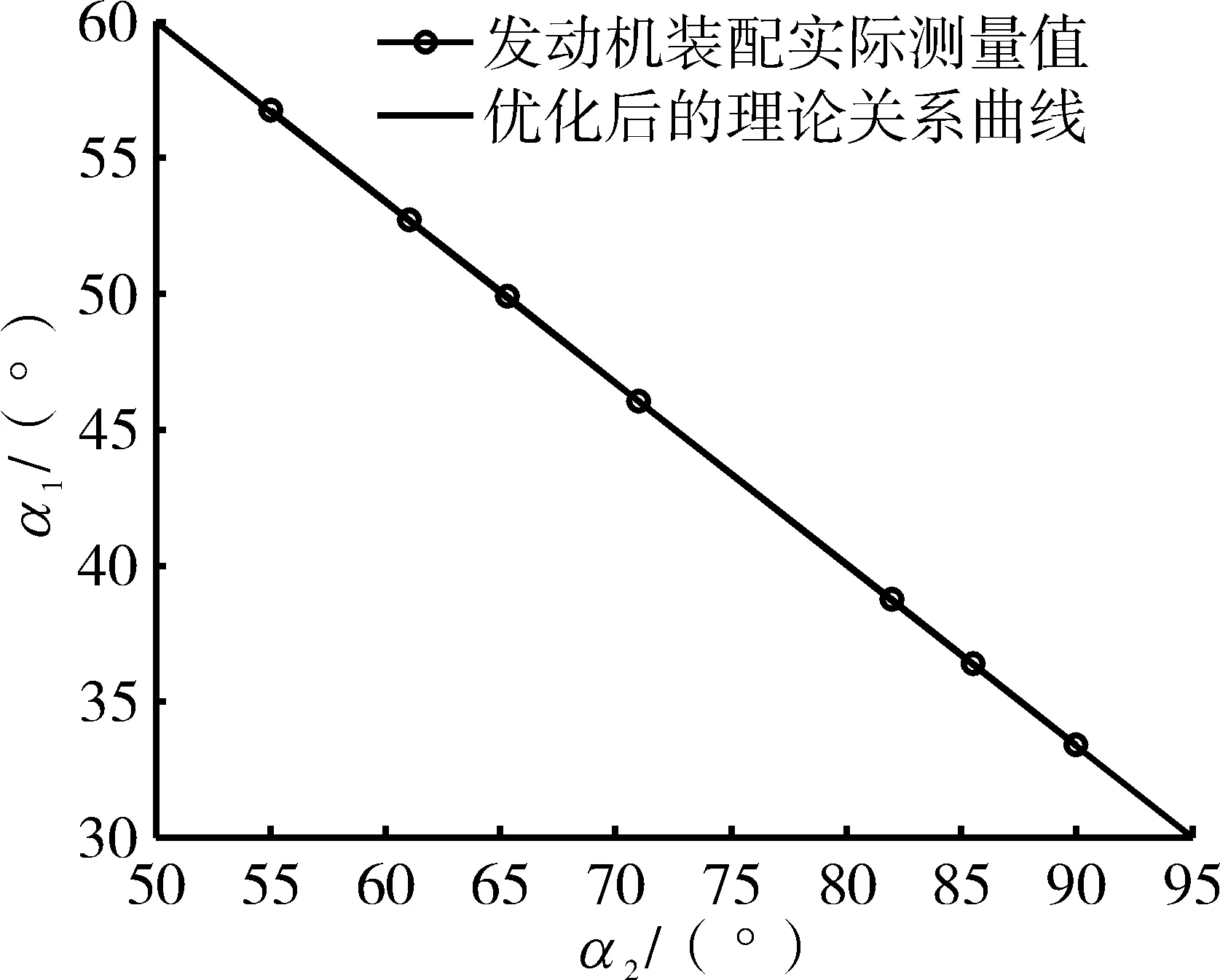
图12 优化后关系曲线和实测结果对比
4 结论
本文对软轴推拉钢索运动的传递关系建立了模型,并通过航空发动机上的应用实例对建模进行了验证,得出结论如下:
(1)基于软轴推拉钢索位移绝对值构建的运动关系传递模型能够准确地描述软轴推拉钢索的运动关系;
(2)通过对航空发动机α2反馈调节机构模型的构建和运动关系的优化设计,表明本方法切实可行;
(3)通过对发动机主泵摇臂初始角度和α2作动机构摇臂长度的调节可以将α2关系曲线变成直线。
