基于图像化变差函数的性能数据异常判别
2019-12-13师利中孙天宇蔡舒妤
师利中,孙天宇,蔡舒妤
(1.中国民航大学航空工程学院,天津300300;2.航天工程大学宇航科学与技术系,北京101416)
0 引言
随着航空发动机智能维修技术的发展,发动机性能监控对于跟踪其性能变化、分析其运行状态、实时预警性能异常具有重要意义。快速存取记录器(Quick Access Recorder, QAR)是飞机上主要的性能数据记录设备,其采集性能数据量大、特征维数高,使得数据分析处理困难,目前对QAR数据的应用还不到其潜在价值的10%。
近年来,针对发动机性能数据处理方法的理论和应用研究不断深入,成果显著。Zhang等[1]提出关联事件QAR超限综合严重程度的GREEN模型,将QAR超限与其并发相关事件相关联;Wang等[2]提出利用QAR数据对典型机载系统进行故障诊断和状态评估,挖掘相应的QAR参数与失效模式之间的关系;杨慧等[3]针对QAR数据集提出1种改进的小波聚类算法CWave Cluster,划分非均匀网格,进一步细化边界网格,对不满足密度阈值的网格进行处理,最终形成聚类;张春晓等[4]利用HOLT双参数指数平滑方法,建立基于机载QAR数据的对称发动机性能参数的差异监控模型,并给出实现对称发动机差异监控的算法;张鹏等[5]提出1种融合卷积神经网络与长短时记忆网络的双通道融合模型CNN-LSTM,使模型能同时表达数据在空间维度和时间维度上的特征。在应用研究方面,Li等[6]将性能监控数据应用于波音飞机空调系统的温度状态预测中;Liang等[7]以民机引气系统为对象,提出引气系统故障检测算法,设计实现了基于QAR数据的民机引气系统健康监测方法;Chen等[8]提出基于QAR数据的飞机纵向飞行控制律辨识机制;LYU等[9]提出1种基于大规模QAR数据的超限风险评估方法;Wang等[10]提出基于QAR数据的航空发动机润滑油消耗率在线监测方法;Gao等[11]提出基于QAR数据的民机发动机起动系统健康监测方法;Sun等[12]提出1种基于时态地理信息系统的FQA方法,对不同时空飞行数据的有效相关性进行分析;孙见忠等[13]提出1种基于涡轮叶片外场故障数据及性能数据的涡轮叶片剩余寿命评估方法,为民航发动机在翼寿命评估及送修方案的制定提供决策支持;谷润平等[14]引入外界环境因素变量,分析发动机燃油流量的影响因素,建立发动机性能异常检测模型。
本文通过引入变差函数研究发动机性能数据的图像转化方法,以融合不同时刻不同参数的性能数据,提升特征表示的关联性和运算效率,并提出了基于变差函数的发动机性能数据异常判别方法,实现发动机性能图像中异常的直观显示和高效判别。
1 性能图像转化方法
为实现发动机性能数据的降维,减小多参数关联性分析的复杂度,需要对性能图像转化方法进行研究。
1.1 性能数据向标准大气条件的换算
发动机性能数据采集于不同的飞行时刻,其高度、气压、温度等环境因素存在较大差异,使得性能数据不具备可比性。因此,需通过标准化方法将性能数据换算到标准大气状态下。
假设性能数据中某性能参数“时间-参数”数据分布图像如图1所示。

图1 “时间-参数”数据分布
可依据对应的高度值对性能参数的分布进行统计,并对其进行曲线拟合,如图2所示。

图2 “高度-参数”数据统计分布
对于性能参数α,假设曲线L为高度-性能参数α拟合曲线,曲线方程为y=f(x)。H0为设定的标准高度,则a0=f(H0)。当α=a1时,对应的高度值为H1,将L平移到a1点的高度,则有曲线L'的方程为

式中:y为曲线方程因变量;x为曲线方程自变量;f(x)为拟合曲线方程;a1为H1高度对应的性能参数取值。
性能参数α的标准化转换公式为
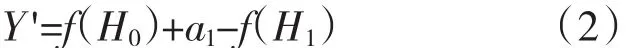
式中:Y'为标准化转换公式。
1.2 性能数据图像化
采用性能图像转化方法将实现性能参数连续值域空间映射到RGB离散彩色空间,如图3所示。

图3 性能数据图像化映射
假设αmax、αmin为标准化修正后性能参数α的最大值、最小值,当α=a时,则性能图像转化公式为

式中:R/G/B为计算所得颜色分量值。
由此形成的性能图像横轴为时间域的表示,纵轴为各参数取值,以实现对不同时刻不同参数的性能数据的融合。
2 基于变差函数的性能图像特征表示
变差函数常用于纹理结构分析和纹理信息的相关性统计[15-16]。不仅可以用于描述低频纹理特征在小尺度上的相关性,还能反映高频纹理信息在大尺度上的结构性。因此,引入变差函数理论对发动机性能图像进行分析,并对关键特征点进行提取,以表示发动机性能图像的特征信息,实现发动机性能多参数关联分析。
假设性能图像大小为M·N,其中任意像素点P坐标为(x,y),对应图像特征值为 I(x,y)。 在尺寸为2d+1的滑动窗口中,窗口中心点设为(x0,y0),变差函数定义为

式中:h为滑动窗口内两点的距离;N(h)为滑动窗口内所有距离为h的点对个数;I(P)为滑动窗口内任意像素点的图像特征值;I(P+h)为滑动窗口内与点P距离为h的像素点的图像特征值。
细化性能图像在 0°、45°、90°、135°4 个方向上变差函数定义为

以 0°、45°、90°、135°4 个方向上的变差函数均值为窗口中心点变差函数值,即该窗口中心像素点(x0,y0)的性能特征值为

对于性能图像,计算其性能特征值,并采用SIFT算法提取关键特征点。利用SIFT方法的多量性,保证在较少的性能图像信息中仍能够提取较为充分的关键特征点。
设第i幅图像Pi尺寸为Mi·Ni,关键特征点共计ni个,第i幅图像第j个关键特征点表示为rij(j=1,2,…,ni),其坐标表示为(xij,yij)。
由于不同性能数据样本数有所差异,生成的性能图像大小有所不同,不同图像间提取的关键特征点坐标不具备可比性,因此需对关键特征点坐标进行处理,转化为相对坐标(x'ij,y'ij)。

式中:xij、yij和 x'ij、y'ij分别为第 i幅图像第 j个关键特征点的横、纵坐标值和横、纵坐标相对坐标值;Mi、Ni分别为第i幅图像长度和宽度。
3 基于变差函数的性能图像异常判别方法
3.1 基于特征值的性能图像差异识别方法
对于任意若干发动机性能图像Pi,选取图像Pk,满足nk=min{ni}。
对于性能图像Pk中的关键特征点r'kl,于其他性能图像Pi中,寻找匹配关键特征点r'ij,满足
发动机性能图像差异距离定义为

发动机性能图像差异距离是识别发动机性能图像差异的标准。
3.2 基于变差函数的性能图像异常判别流程
基于变差函数的发动机性能异常判别方法具体流程如图4所示。
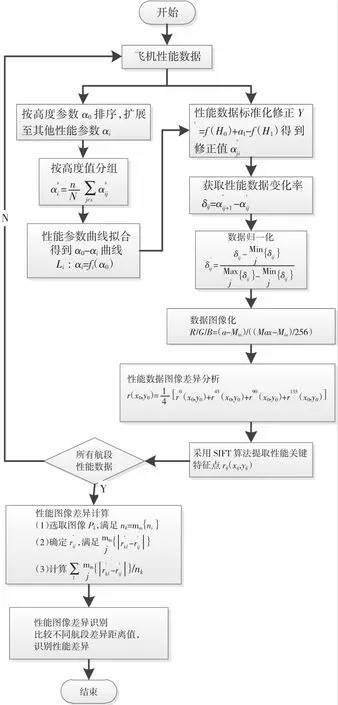
图4 方法流程
设N表示发动机性能数据样本数量,αi表示发动机性能数据中第i个性能参数,其中α0为高度参数,αij表示第i个性能参数第j个数据的取值。
(1)按高度值排序。对高度参数α0进行排序,并扩展至其他性能参数αi。
(2)按高度值分组。按高度参数α0将发动机性能数据样本分为n组,计算每个性能参数分组后取值。表示第i个性能参数的第s组。对应取值为=
(3)性能参数曲线拟合。对每个性能参数αi分组后取值进行曲线拟合,得到α0-αi曲线Li:αi=f(α0)。
(4)性能数据标准化修正。对每个性能参数αi,将拟合曲线方程Li:αi=f(α0)代入式(2),得到性能参数αi数据标准化修正方程,进行性能数据标准化修正。αij表示标准化修正后第i个性能参数第j个数据的取值。
(5)获取性能数据变化率。对每个性能参数αi,获取其性能变化率 δij=αij+1-αij。
(6)数据归一化。对每个性能参数δij,进行数据归
(7)数据图像化。对每个性能参数 αi,依据式(3),得到发动机性能图像。对于性能参数数量较少的情况,形成图像时可放大映射。
(8)性能图像特征表示。对性能图像中所有像素点 P(x,y),依据式(5)~(11)计算得到各像素变差函数值r(x,y)。
(9)性能关键特征点提取。采用SIFT算法提取关键特征点,获取关键特征点坐标,并进行相对坐标处理。
(10)对所有性能数据进行性能图像转化及关键特征点提取。
(11)发动机性能图像差异计算。选取性能图像中,关键特征点数最少的图像;对于其他性能图像,根据式(12),计算关键特征点差异距离。
(12)不同航段性能图像差异识别。比较不同性能图像差异距离值,在发动机不同运行状态下的差异距离值有明显变化,以此识别发动机性能差异。
4 方法验证与结果分析
飞机的起飞、进近和着陆阶段约占总飞行时间的17%,但其事故发生概率高达78%。为验证基于图像化变差函数的发动机性能数据异常判别方法,选取某机型飞机起飞阶段性能数据为实例,共计4组数据样本量见表1。性能数据包含21个性能参数,分别为:2台发动机的增压比REP(engine pressure ratio)、低压转子转速N1(low pressure compressor rotor speed)、高压转子转速N2(high pressure compressor rotor speed)、排气出口温度TEG(exhaust gas temperature)、燃油流量FF(fuel flow)、油门杆角度ATL(throttle lever angle)、滑油流量Oq(oil quantity)、滑油压力Op(oil pressure)、低压转子振动值N1V(low pressure compressor rotor vibrate)、高压转子振动值 N2V(high pressure compressor rotor vibrate)。在4组数据样本量中,3组为正常起飞状态数据;1组为异常起飞状态数据,起飞阶段推油门至40%N1时,出现警告终止起飞。

表1 起飞阶段性能数据实例样本
首先依据性能图像转化方法对实例数据进行预处理,将高维度性能数据转化成2维性能图像,获得实例数据对应性能图像,如图5所示。
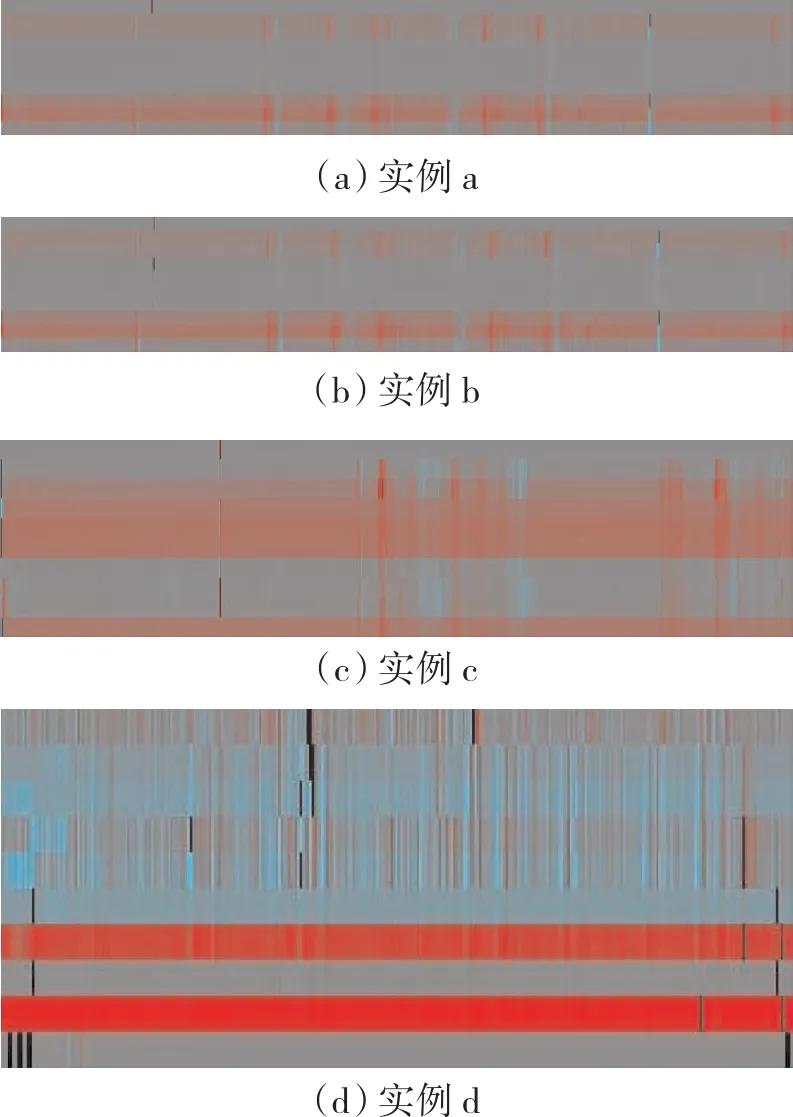
图5 4个实例性能图像转化结果
从图 5(a)~(c)中可见,对于正常起飞阶段,经标准化修正后性能参数较为平稳;转化的性能图像各参数对应图像区域,没有明显颜色变化;局部存在由飞行高度引起的轻微波动。
从图5(d)中可见,对于异常中断起飞状态下的性能图像,PER、N1、N2、TEG、FF等 5 个性能参数所对应的图像区域色彩波动明显,Oq、N1V2个参数值明显高于正常状态。
依据式(9),对发动机性能图像计算其性能特征值,实现实例图像进行特征表示;分别采用Harris方法和SIFT方法对特征表示后的性能图像提取关键特征点,结果图像如图6、7所示。

图6 Harris方法提取关键特征点
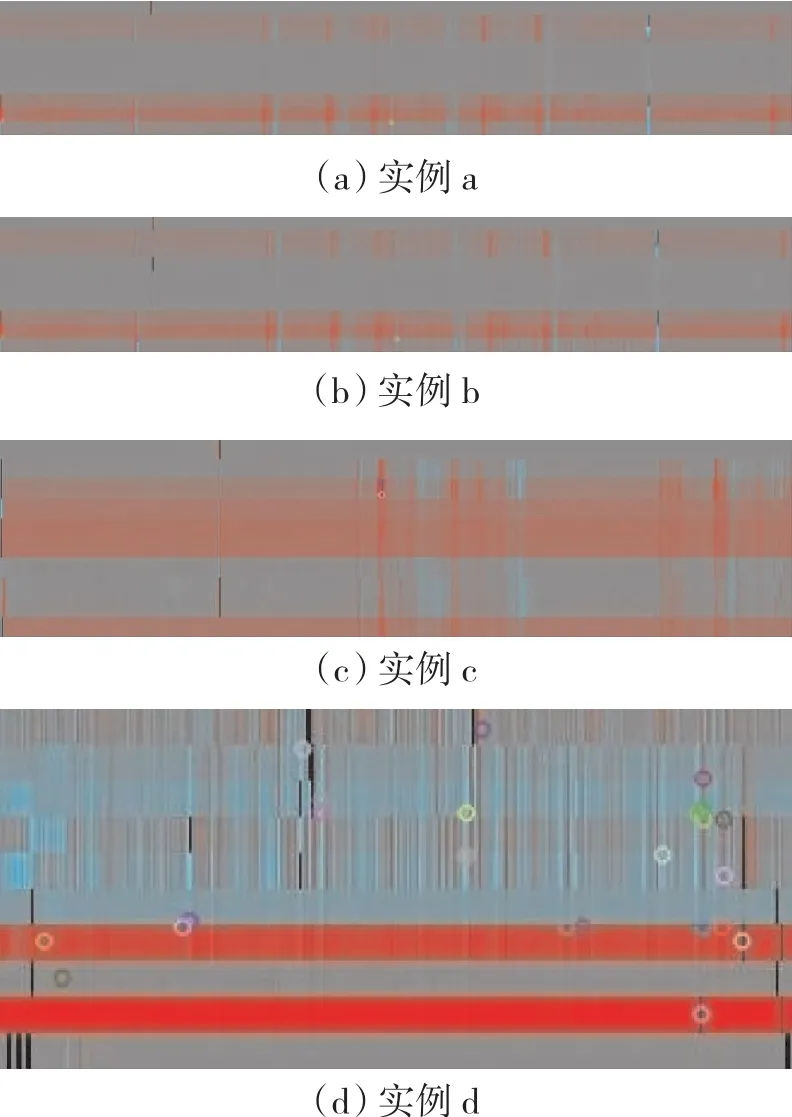
图7 SlFT方法提取关键特征点
从图6、7中可见,对于信息并不充分的发动机性能图像,SIFT方法所提取的特征点明显比Harris方法数量多,为后续性能特征分析提供了数据保证。
由于实例性能数据样本量不同,需将关键特征点坐标转化为相对坐标,依据式(10)、(11),对 SIFT 方法所提取的关键特征点转化为相对坐标,散点如图8所示。
根据关键特征点匹配并计算差异距离值,结果见表2,该方法运算时间如图9所示。

图8 关键特征点相对坐标散点

表2 关键特征点差异距离值

图9 实例运算时间
由关键特征点相对坐标散点图和差异距离值可见,实例a、b在关键特征点分布上有较大的相似性,差异距离值极为接近,可由此判断其运行状态具有较高的一致性。
实例c与a、b在关键特征点数量上有所差异,但三者差异距离值较为接近,因此三者应处于相同运行状态。
实例d与其他实例关键特征点分布存在较大差异,差异距离值偏差较大,由此可判断其运行状态与其他实例不同。
假设已知其中1个实例的状态,即可判断出其他实例的状态。
从运行时间来看,图像化、特征表示、特征提取阶段所需计算时间相对较长,异常识别阶段均在毫秒级时间范围内完成运算过程,总体运行效率较高。
5 结论
本文通过研究发动机性能图像转化方法,结合变差函数理论,提出了1种基于图像化变差函数的发动机性能数据异常判别方法,并以发动机实际性能数据为实例,进行了方法验证。由验证结果可知:
(1)从运算速度方面,本文方法能够在毫秒级时间范围内完成各阶段运算过程,时间复杂度较低。
(2)从异常判别质量方面,可依据关键特征点分布和差异距离值,实现对不同性能图像特征的分类,从而实现对应性能数据运行状态的自动判别。
(3)本文方法为发动机性能数据的智能监控与机器分析提供了数据基础,后续将对性能特征的完备表示、机器分析进一步研究,以提高发动机性能监控的智能化程度。
