科技创新驱动柳州制造业转型升级的实证研究
2019-12-12张光明魏锋
张光明 魏锋


[摘 要] 基于2003-2017年柳州市专利授权数和工业增加值数据,运用ADF检验、VAR模型脉冲响应函数分析、协整检验与误差修正模型等方法对科技创新驱动柳州制造业转型升级之间的关系进行了实证研究。结果表明,柳州市科技创新与制造业发展之间的长期稳定关系显著,而科技创新对柳州制造业发展的短期影响关系不显著,但长期影响持续有效,科技创新与柳州制造业发展之间的短期波动偏离二者长期关系的程度并不高。柳州市应发挥科技创新在制造业转型发展中的引领和驱动作用,持续加大科技创新投入,加快科技创新成果转化,积极引导各种创新要素聚集到企业,促进企业成为创新决策和创新成果转化的主体,全面提升企业的自主创新能力,最终实现制造业的全面转型升级。
[关键词] 科技创新;制造业转型升级;协整
[中图分类号] F204[文献标识码] A[文章编号] 1009-6043(2019)11-0054-02
科技创新与制造业转型升级之间的关系一直是众多学者的研究热点。李胜文等(2016)利用1998-2010年制造业企业经验数据进行实证分析,发现科技创新对产业升级具有显著贡献[1]。杨智峰等(2014)通过建立投入产出模型分析各产业部门产出增长发现,科技进步推动了2002-2007年的产业结构优化升级[2]。王维(2012)认为中国工业转型升级的制约因素之一就在于科技创新效益不高[3]。李杰(2009)在研究产业结构演进的一般规律后发现,技术密集化和信息化将是制造业发展的方向及其结构演进的核心动力[4]。以上研究大多基于国民经济产业角度,而且主要针对发达地区,缺乏对区域经济特别是欠发达地区科技创新与制造业发展关系的深入研究。本文以中国西部工业城市——广西柳州市为研究对象,对其科技创新与制造业发展关系进行了实证研究,以期能为该地区科技创新驱动制造业的转型升级提供理论参考和政策建议。
一、指标选择与数据处理
(一)指标选择
现代制造业科技创新成果的主要表现形式为专利,考虑数据的可得性,因此选用专利授权数(文中记为ZL)作为科技创新水平的衡量指标。由于制造业属于工业的主要产业门类,考虑数据的可得性,因此选用工业增加值(文中记为GY)作为制造业发展水平的衡量指标。
(二)数据来源和处理
本文选择2003-2017年柳州市专利授权数与工业增加值数据(原始数据均来源于各年度《柳州市国民经济与社会发展统计公报》),为消除原始数据序列可能存在的异方差性,同时不改变两个指标之间的长期关系,本文对专利授权数ZL与工业增加值GY两个指标原始数据均作了自然对数变换处理,处理后的数据序列分别记为LNZL与LNGY,所有数据见表1。
二、科技创新驱动柳州制造业发展关系的实证分析
(一)变量的平稳性检验
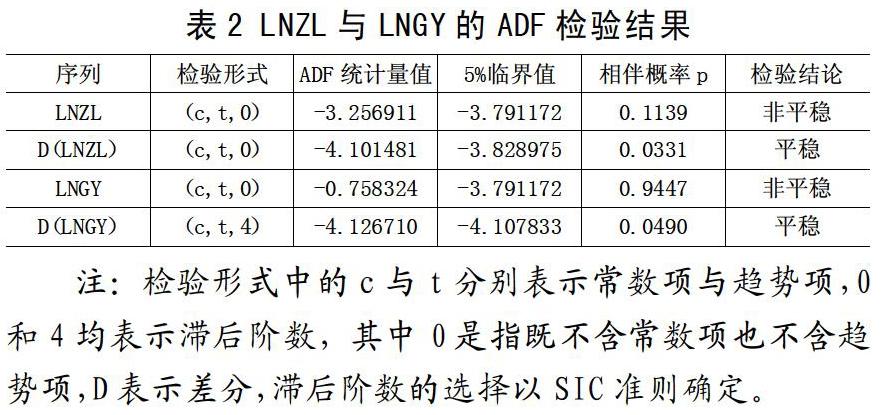
經典回归分析理论要求所使用的时间序列数据满足平稳性特征,否则对不平稳时间序列数据直接使用回归分析会产生“伪回归”的不合理现象,计量经济学中解决该问题的办法是对数据进行平稳性检验,ADF检验就是一种常用的数据平稳性检验方法,本文使用Eviews7.0对LNZL与LNGY分别进行了ADF检验,检验结果见表2。
由表2可知,LNZL与LNGY的ADF统计量绝对值小于其5%临界值的绝对值,同时相伴概率p也均大于5%,说明两个数据序列在显著性水平为5%时均不平稳,但是两个差分数据序列D(LNZL)与D(LNGY)在显著性水平为5%时均为平稳序列,由此证明LNZL与LNGY两个均属于一阶单整数据序列,二者之间可能会存在协整关系。
(二)VAR模型及脉冲响应函数分析
1.VAR模型
VAR是一种常用的计量经济模型,它是用模型中的当期变量对所有变量的若干滞后变量进行回归,一般用来估计多个内生变量间的动态关系。VAR建模无需任何关于变量的约束条件,但需确定变量的滞后阶数,一般通过LR、FPE、AIC、SC与HQ五种检验准则进行比较来选择最优滞后阶数,本文使用Eviews7.0分别得到五种准则的检验结果,并在各准则最优滞后阶数对应的检验值右上角标注星号,所得结果如表3所示,显然五种准则确定的最优滞后阶数均为3,因此本文可得一个VAR(3)模型,同时可由VAR估计结果知该模型所有特征根均落在单位圆内,表明该VAR模型结构是稳定的,可以进行脉冲响应函数分析。
2.脉冲响应函数分析
脉冲响应函数描述了VAR模型中每个内生变量的一个标准差冲击对自身及其他内生变量所造成的影响。在VAR模型中第i个内生变量的一个冲击不仅直接影响其本身,而且通过VAR的动态结构传递给其他的内生变量,脉冲响应函数刻画的就是这种影响的轨迹,从而显示任意一个变量的扰动是如何通过模型影响所有其他变量,最终又反馈到本身的过程[5]。本文使用Eviews7.0得到了LNGY的脉冲响应表(见表4)。
(三)协整检验
协整检验是常用来处理非平稳变量数据之间是否存在长期均衡关系的计量分析方法,关于两变量之间的协整检验常用方法是EG两步法,具体如下[6]:
第一步,根据两个变量数据进行OLS回归,本文以LNZL为解释变量,以LNGY为被解释变量,运用Eviews7.0进行了回归分析,结果见表5。由表5可知,回归方程拟合优度较高(可决系数R2=0.870416),自变量LNZL对应回归系数(0.689125)的相伴概率接近0说明该回归系数很显著,回归方程的F值(87.32090)很高同时相伴概率接近0说明整个回归方程效果显著[6]。
第二步,对所得回归方程的残差序列进行平稳性检验,如果残差序列属于平稳序列,第一步所建立的回归方程是有效的,表明变量间的协整关系成立。本文运用Eviews7.0对该残差序列进行了ADF检验,结果见表6。由表6可知,残差序列的ADF检验统计量值小于5%显著性水平下的临界值,表明在5%显著性水平下残差序列是平稳序列,这说明LNZL和LNGY之间存在协整关系[6],即科技创新对柳州制造业转型发展的影响关系是长期稳定的,这与前文脉冲响应函数分析得出的结论是一致的。
(四)误差修正模型
协整回归方程反映的是变量之间的长期均衡关系,这种长期关系实际上是在短期关系的不断累计中形成的。根据Granger表述定理,如果两个变量之间是协整的,则它们之间的短期非均衡关系一定可以通过一个误差修正模型(ECM)来描述[7]。本文借助Eviews7.0建立了LNGY与LNZL的以下误差修正模型:
Δ(LNGYt)=0.177815-0.053051Δ(LNZLt)-0.11177ecmt-1
其中误差修正项ecmt-1=LNGYt-1-0.689125LNZLt-1
-1.918557,它反映了变量在短期波动中偏离其长期均衡关系的程度。误差修正模型反映了前文中协整方程因变量LNGYt的短期波动Δ(LNGYt)受两个因素影响:一是自变量LNZLt的短期波动Δ(LNZLt)带来的影响,二是误差修正项ecmt-1的影响。误差修正项ecmt-1的系数-0.11177为负,这种负向修正机制可以这样去解释:当LNGYt-1大于其长期均衡值时ecmt-1为正,则Δ(LNGYt)减小,使得LNGY对其长期均衡值的偏离减弱;当LNGYt-1小于其长期均衡值时ecmt-1为负,则Δ(LNGYt)增大,使得LNGY对其长期均衡值的偏离增强,无论出现哪种情况LNGY与LNZL之间的长期均衡关系均得以维持。误差修正系数-0.11177反映了LNGY与LNZL之间的短期波动中有大约11%会在下一年获得修正[7],这说明科技创新与柳州制造业转型发展之间的短期波动偏离二者长期均衡关系的程度并不高,此结论与前文脉冲响應函数分析不谋而合。
三、结论与建议
本文运用ADF检验、VAR模型脉冲响应函数分析、协整检验与误差修正模型等方法对科技创新驱动柳州制造业转型升级之间的关系进行了实证研究。其中,ADF检验发现柳州市专利授权数和工业增加值均为不平稳序列,但二者的一阶差分序列均为平稳序列;VAR模型脉冲响应函数分析表明科技创新对柳州制造业转型发展的短期影响不稳定,但长期影响是持续有效的;协整检验进一步证明柳州市科技创新与制造业发展之间存在显著的长期均衡关系,科技创新对柳州制造业转型发展的促进作用是长期稳定的;误差修正模型显示科技创新与柳州制造业转型发展之间的短期波动偏离二者长期均衡关系的程度并不高。因此,柳州市应始终坚持科技创新在制造业转型发展中的引领和驱动作用,持续加大科技创新投入,加快科技创新成果转化力度,积极引导各种创新要素聚集到企业,促进企业成为创新决策和创新成果转化的主体,全面提升企业的自主创新能力,最终实现制造业的全面转型升级。
[参考文献]
[1]李胜文,杨学儒,檀宏斌.技术创新、技术创业和产业升级——基于技术创新和技术创业交互效应的视角[J].经济问题探索,2016(1):111-117.
[2]杨智峰,陈霜华,汪伟.中国产业结构变化的动因分析——基于投入产出模型的实证研究[J].财经研究,2014(9):38-49.
[3]王维.全球视角下的中国工业转型升级制约因素分析[J].亚太经济,2012(4):66-70.
[4]李杰.产业结构演进的一般规律及国际经验比较[J].经济问题,2009(6):31-34.
[5]张光明.广西物流业与制造业联动关系的实证研究[J].物流技术,2014(5):201-220.
[6]张光明.广西区域物流与区域经济互动关系的实证分析[J].物流技术,2014(6):121-140.
[7]张光明,廖志高.广西港口物流与对外贸易关系的实证研究[J].物流技术,2015(6):93-95.
[8]高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2009.
[责任编辑:史朴]
