内压和地震同时作用下的核电站安全壳响应分析

2019-12-12彭齐驭刘玉岚王彪

中山大学学报(自然科学版)(中英文) 2019年6期

彭齐驭，刘玉岚，王彪

(1.中山大学航空航天学院，广东广州 510006；2.中山大学中法核工程与技术学院，广东广州 510275)

我国能源结构不平衡，核电作为少数技术较为成熟的重要清洁能源，一直是我国战略性发展的重要方向[1]。核电事故的危害性使得核电站的安全性要求较一般建筑结构要高得多。而，安全壳作为核电站发生事故时屏蔽放射性物质的最后屏障，必须满足安全性的高要求。2011年日本福岛核事故发生以来，应对高强地震成为了核电站安全设计越加重视的问题[2]。另外，因冷却系统管道破裂产生高压气体、严重事故下核燃料包壳锆水反应产生的氢气以及其他原因产生的巨大压力，也会对核电站安全产生较大的威胁[3]。极端情况下，地震和内压有可能同时作用于核电站系统，如：高强地震诱发主蒸汽管道破裂同时对安全壳产生影响等。在现有的研究成果当中，有许多仅考虑地震作用的安全壳分析。地震响应分析主要采用反应谱分析法和时程分析法，如：Dundulis等[4]使用反应谱法计算Ignalina核电站楼层地震响应；Ahme等[5]使用时程分析法探究核电站内剪力墙在周期荷载下的响应。核电站安全壳在内压作用下的承载力分析也有报道，如：张会东等[6]使用ANSYS进行核电站安全壳的位移和应变分析。从整体来看，考虑两者同时作用的相关研究较少。因此，本文针对核电站的CPR1000建立了精细三维有限元模型，使用ABAQUS分析软件，计算了单独地震、单独内压、以及不同地震与内压组合作用时的安全极限，以及地震与内压组合作用时核电站安全壳的响应规律。

1 模型与设置

1.1 安全壳模型外观尺寸

CPR1000核电站安全壳，主要由扁球壳形穹顶、筒体和筏板基础三部分组成，内置0.006 m的钢衬里。模型参照文献[7]的数据，安全壳的总高度为66.68 m。上部穹顶半径为24 m，中部筒体壁厚0.9 m，内径为37 m，筒体上部与壁厚为0.8 m的穹顶相连接。筒体中部还设有一个直径为7.4 m的设备闸门孔，中部偏下和底部分别设置一个直径为2.94 m的人员闸门孔。设备闸门孔作额外加固，筒体壁沿互相垂直的x、y方向各设置两扶壁柱，顶部设环梁。安全壳的几何剖面图如图1所示。

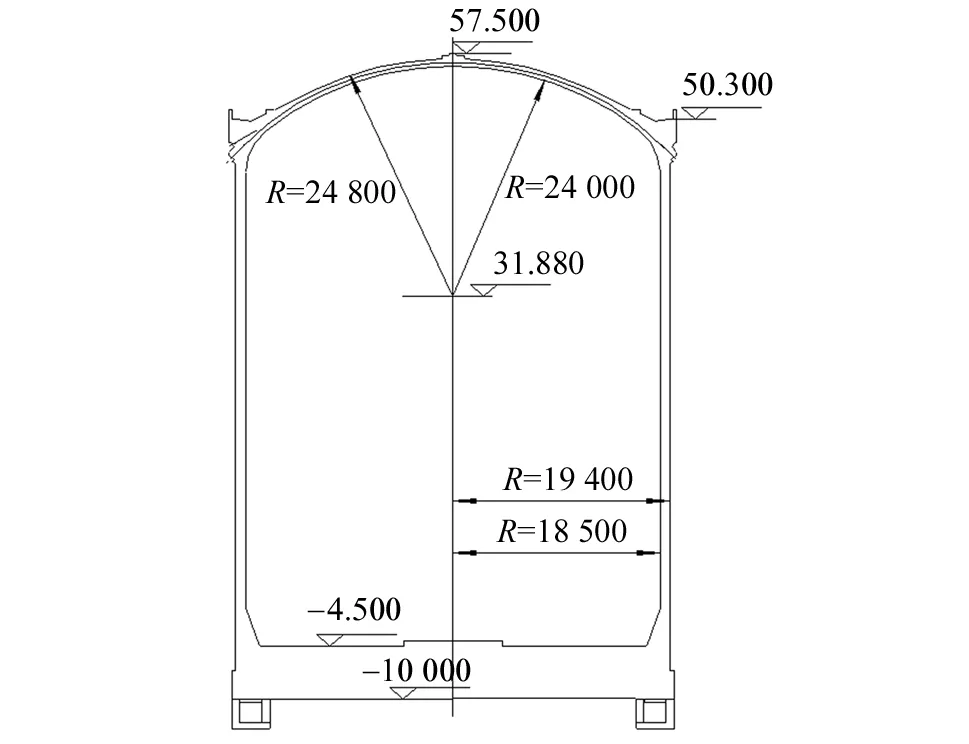
图1 安全壳几何剖面图Fig.1 Geometric profile of containment

1.2 计算模型

本文采用ABAQUS有限元分析软件进行安全壳的非线性分析。穹顶、筒体及基础混凝土部分采用三维八节点的实体单元C3D8R单元模拟。预应力筋采用T3D2杆单元模拟。普通钢筋采用ABAQUS内置的rebar surface层模拟，使用SFM3D4R面单元。钢内衬结构在混凝土内侧模型上设置了一层skin面模拟，并选用S4R壳单元类型。整体三维有限元模型如图2所示。

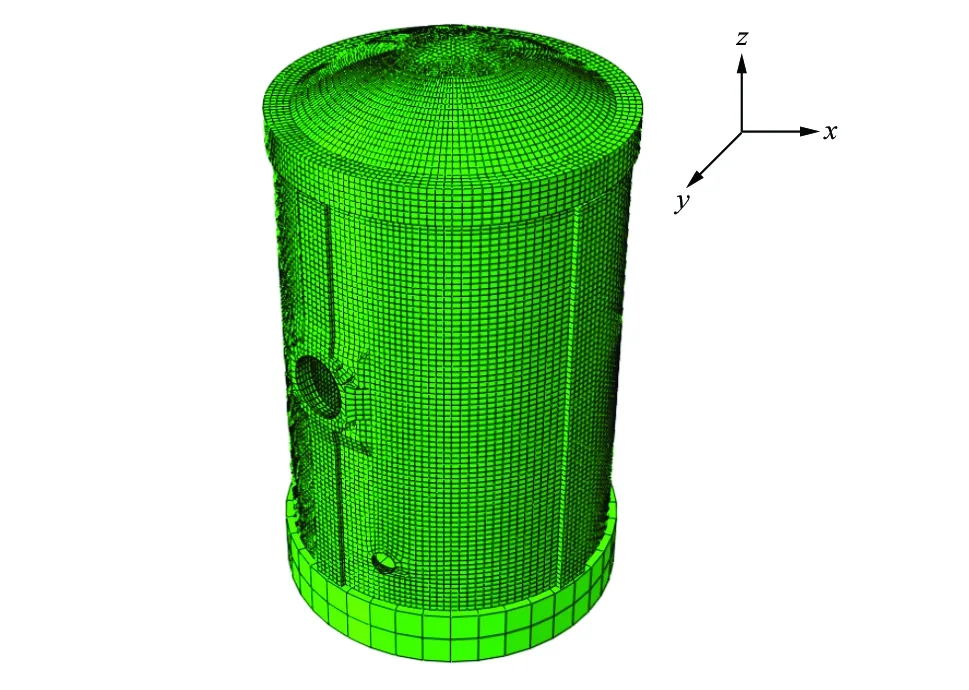
图2 安全壳三维有限元模型Fig.2 3D finite element model of containment

1.3 材料属性

核电站安全壳为预应力混凝土结构，混凝土强度等级采用C50。考虑混凝土结构的非线性，在实际有限元数值模拟分析中，采用ABAQUS的塑性损伤模型模拟混凝土的性质[8]。为了计算方便，忽略钢筋与混凝土的滑移，用钢筋层直接嵌入到混凝土的形式模拟钢筋与混凝土的黏结。普通钢筋包括壳体的内中外三层、扶壁内的普通钢筋以及在设备闸门口附近设置的加强筋。普通钢筋采用ABAQUS中rebar surface层来模拟；而，预应力钢筋则采用降温法实现，即设置线膨胀系数和降温使得钢筋收缩产生预应力。预应力钢束的空间定位和钢束预应力值的确定参考文献[9]。通过对钢束空间几何曲线方程的推导和数值计算，最终确定的预应力钢束如图3所示。具体材料属性见表1。

表1 安全壳结构各部件的材料特性Table 1 Properties of each component of the containment

图3 预应力钢束Fig.3 Model of prestressed tendons

1.4 地震荷载

根据我国《核电厂的抗震设计与鉴定》，要求核电站对厂址按照每年10-4超越概率(万年一遇)的地震水平进行设防。而，现今我国主要厂址万年一遇的地震水平大都低于0.2g，少数在0.2g～0.3g之间[10]。一般取0.2g作为标准设计基准地震水平，即水平方向地面峰值加速度设置为0.2g，竖直方向峰值加速度为水平方向的2/3。本文采用人工合成的30 s LBNS基准地震波作为荷载输入，如图4所示。LBNS地震波是根据美国长滩时程记录加上人工修正得来的，此地震时程的反应谱能够包络美国RG1.6标准反应谱。

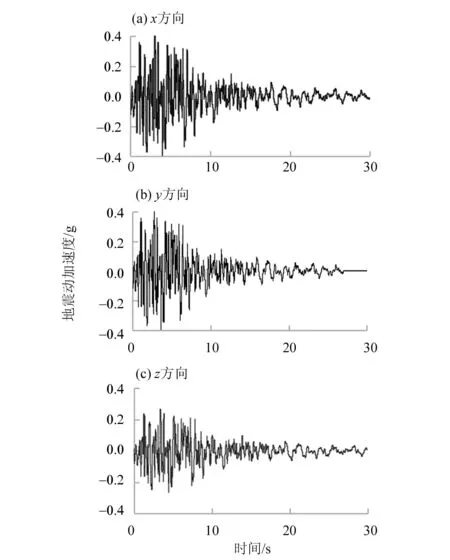
图4 LBNS人工地震波Fig.4 LBNS artificial seismic wave

1.5 假设以及边界条件

假设地震动荷载直接施加于核电站圆形阀板基础底部，安全壳主体直接固接在底部基础，而内压则平均作用于安全壳内部表面。本次分析不考虑土-结构的相互作用、底部基础变形、安全壳外围建筑的影响，以及安全壳内部设备等对安全壳的作用。依据参考文献[11]，钢筋混凝土结构的临界阻尼比一般是在3%～8%之间，这里临界阻尼比取为3%。由模态分析和时程分析可以发现：x、y方向的模态、加速度、位移响应结果类似，而z方向响应远小于水平方向。因此，仅以x方向响应作为考察对象，并通过安全壳的加速度、位移和应变响应来探究安全壳的安全极限。对于安全壳的失效判断，考虑最坏情况，即反应堆内散热系统失效、紧急停堆失效、堆芯熔融损坏反应堆压力容器或释放放射性物质。在其他内部措施失效的情况下，作为防止放射性物质扩散的最后屏障，安全壳务必须保持完整屏蔽。一旦混凝土开裂区域贯穿安全壳，在钢内衬未能完全保护的情况下，即使未达到钢筋混凝土安全壳的承载极限，亦有产生核泄漏的危险。因此，本文以此种情况为核电站安全壳的核泄漏安全极限，参照文献[12]有关混凝土开裂的应变值，取1.5×10-4。一般, 地震响应计算主要分为时程分析法和地震反应谱法。一般的多自由度体系有以下动力方程：

(1)

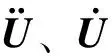
(2)

(3)

(4)

{φj}为第j阶模态，γj、ωj、ξj分别为第j阶模态的参与系数、固有频率和阻尼比。而地震反应谱法则直接得到第j振型在有地震条件下的影响系数αj，并得到地震作用力：

Fji=|Fji(t)|max=αjγjφjimig

(5)

再通过振型叠加得到最终解。为了更精确地分析，本文在现行的反应谱法的基础上采用时程分析法的最终加速度与位移响应结果，即：选取安全壳外壁不同高度处各点在整段地震时长中的加速度和位移响应最大值作为安全壳响应代表值。且，由于在塑性假设中混凝土开裂后抗拉能力急剧降低，故通过混凝土的应变进行分析。应变分析选取整段地震时长中安全壳应变响应最大时的最大主应变分布作为代表值。

2 仅考虑地震作用的响应分析

实际地震不但对核电站安全壳，同时对安全壳内部设备也具有较大的危害。因此，一方面需考察地震下安全壳的应力应变分布，另一方面还需较准确地计算安全壳的地震加速度和位移响应。本文主要分析标准设计基准地震(0.2g)到两倍标准设计基准地震(0.4g)时安全壳的地震响应。

2.1 模态分析

通过模态法进行结构的自振频率、振型等动力特性分析，反映地震响应特性。表2是安全壳结构前16阶模态频率信息。

安全壳的第一阶振型、第二阶振型分别以x方向和y方向为主，对应频率分别为4.245 Hz和 4.262 Hz，两个方向的频率近似相同；实际结构在x方向和y方向的动力响应也接近；而以竖直z向为主的振型出现在第十二阶模态，x和y方向是结构的主要运动方向。因而，本文仅考察x方向上的响应。

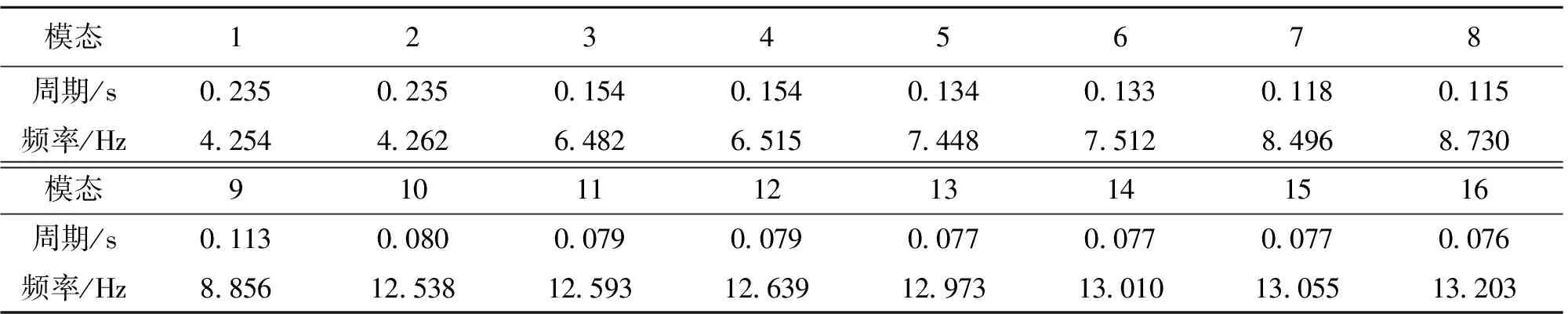
表2 安全壳结构前16阶振动特性Table 2 First 16 order vibration characteristics

2.2 加速度与位移响应

如图5所示，随着地震强度不断提高，安全壳的加速度响应与高度的斜率越来越大。另一方面，加速度响应曲线由0.2g时的线性逐渐变为非线性。地震动峰值加速度为0.2g时，安全壳尚未有任何部分进入塑性区，整体响应呈线性分布。但，进入地震动峰值加速度较高的地震荷载，如0.4g时，在高度为10～30 m的筒体中段，可以明显看到非线性的增长，这说明安全壳的局部进入塑性阶段。

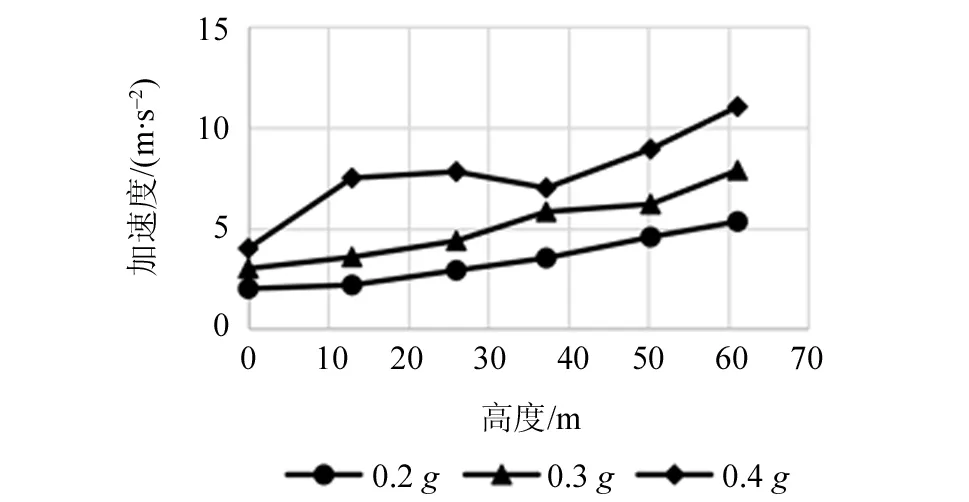
图5 核电站安全壳地震加速度响应Fig.5 Seismic acceleration response of containment

从图6可以看到，随着地震强度增大，安全壳位移响应仍沿高度方向线性递增。另外，地震达到0.4g时，安全壳局部进入塑性阶段，所得位移响应在15 m和25 m高度处略有增加，但位移响应整体仍呈线性增加。这说明核电站安全壳除局部进入塑性阶段外，整体结构仍处于弹性阶段。

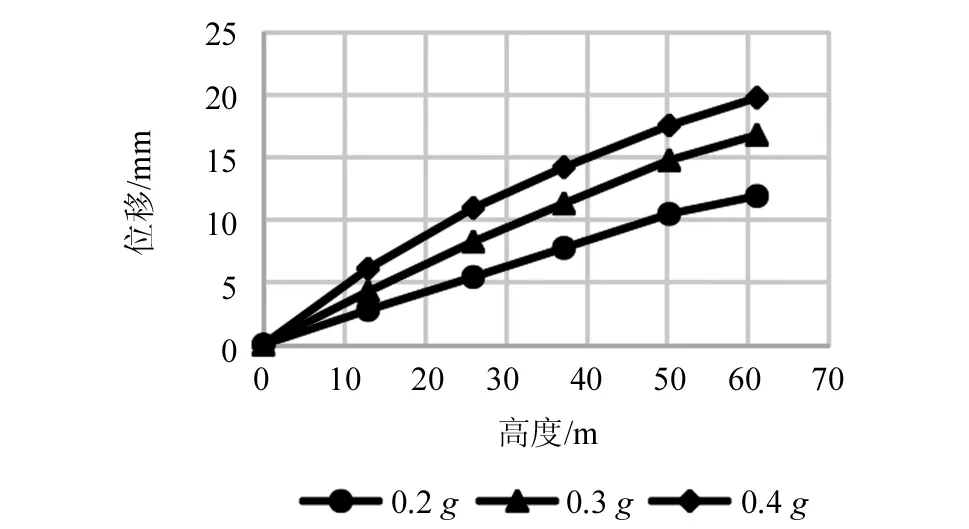
图6 核电站安全壳地震位移响应Fig.6 Seismic displacement response of containment

2.3 应变响应分析

安全壳混凝土部分的最大主应变分布，如图7所示。在图7(a)中，地震动峰值加速度为0.2g时，安全壳大部分区域未达主拉应变极限值；在如图7(b)中，地震动峰值加速度为0.3g时，安全壳中部设备闸门孔附近区域开始出现局部开裂，但并未贯通壁面。在如图7(c)中，当地震水平提高至0.4g时，安全壳底部变截面区域(图右下)最先出现开裂区域贯通安全壳壁面，紧接着底部人员闸门孔处壁面也被贯通，底部区域逐渐连成开裂区域带。由此可知，安全壳底部变截面位置与底部人员闸门孔在地震作用下容易发生应力集中而最先到达极限；随着地震强度继续增加，将出现混凝土开裂贯通区域。因此，在仅有地震作用时安全壳的安全极限为0.4g。安全壳地震响应应力主要集中在底部，包括底部变截面区和底部人员闸门孔。且，在地震达到0.4g前，未出现放射性物质泄漏的危险，安全壳未失效。

图7 安全壳在不同强度地震作用下的最大主应变分布图Fig.7 Maximum principal strain distribution of containment under different earthquakes

3 仅考虑内压作用的安全壳分析

在人为失误、设备局部疲劳或其他非地震因素下也可能发生冷却管道破裂、堆芯熔融、锆水反应等事故，最终使得安全壳内压大大增加。本文在安全壳内表面均匀施加0～130 kPa的内压，并考察安全壳的应变。

由于开裂区域最先贯通于中下部的人员闸门孔和中部设备闸门孔两侧，作此处的剖面图考察最大主应变分布。当内压在100 kPa以下时，混凝土主应变分布基本未达到开裂极限。当内压达到100 kPa时，混凝土安全壳中部设备孔处附近开始出现应力集中，局部达到混凝土拉应变极限，但未贯通安全壳，如图8(a)所示。在内压为110 kPa时，中下部的闸门孔(图片右下)开始逐步逼近开裂极限，如图8(b)所示。在内压为120 kPa时，闸门孔达到开裂极限，并贯通安全壳内外表面，出现放射性物质泄漏的危险，安全壳失效，如图8(c)所示。在图8(d)中，在内压为130 kPa时中部设备孔两侧开裂区域也贯通混凝土壁面，安全壳壁面再也无法作为放射性物质的屏蔽保护措施。因此，仅考虑内压作用时120 kPa为安全壳的内压失效极限；而且，应力主要集中在中部包括中部设备孔和中下部闸门孔。因安全壳在120 kPa后已经失效，将内压在120 kPa以内作为设置条件。

图8 安全壳在不同内压作用下的最大主应变分布图Fig.8 Maximum principal strain distribution of containment under different internal pressure

4 地震和内压同时作用时的安全壳响应

4.1 不同内压作用下的地震响应

4.1.1 加速度与位移响应考虑标准设计基准强度的地震作用下，不同内压对安全壳响应的影响。地震作用设置为0.2g，同时施加0～150 kPa的内压，并分析安全壳的应变响应。当安全壳内部压力逐渐增大时，安全壳的刚度也将慢慢增加，加速度与位移响应将有所变化。由图9～10可以看到，随着内压的增大，安全壳的加速度和位移变化较小，这说明实际压力对加速度与位移的影响并不大。在内压达到100 kPa时，加速度响应开始有所变化，如高度为12.96 m处(闸门孔位置)的加速度。这是因为安全壳在内压作用下开始有局部屈服并开始进入塑性阶段。因此，内压小于100 kPa时可不考虑地震加速度和位移响应的变化对内部设备的影响。

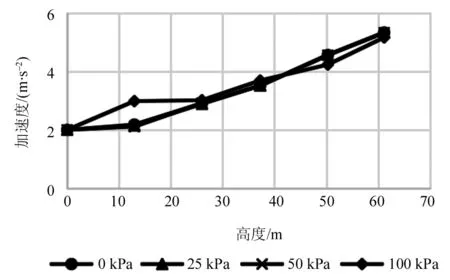
图9 不同内压作用下安全壳的地震加速度响应Fig.9 Seismic acceleration response of containment under different internal pressure

4.1.2 应变响应分析由图11可以看出，内压小于50 kPa的阶段，安全壳仅在设备孔处有局部应力集中，整体尚未达到极限拉应变的区域；内压达到75 kPa时，中下部闸门孔附近开始出现应力集中的区域，主应变值较高，如图11(c)所示。在内压达到100 kPa时，中下部闸门孔(图右下)最先被开裂区域贯通，然后底部闸门孔和中部设备孔两侧也依次贯通，安全壳失效，如图11(d)所示。对比仅有内压作用时安全壳出现开裂贯通区域的内压(120 kPa)，发现其安全极限下降了16.7%。

4.2 不同地震强度下的响应分析

4.2.1 加速度与位移响应考虑较小内压下，不同地震强度对安全壳响应的影响。伴随着地震强度增大，很可能发生冷却系统管道破裂或锆水反应产生大量氢气，导致内压大大增大的情况。内压设置为50 kPa，同时施加0.2g～0.4g的地震荷载，分析安全壳的应变响应。同上节一样，在100 kPa以下的内压作用下，安全壳的加速度和位移并无显著变化，因此不作另外详述。

4.2.2 应变响应如图12，随着地震动加速度的不断增大，安全壳应变响应不断增大。当地震强度为0.2g时，安全壳混凝土尚未达到开裂极限。当地震强度为0.25g时，虽然设备孔处有局部开裂，但开裂区域仍未贯通壁面。当地震强度达到0.3g时，安全壳底部闸门孔被开裂区贯通，底部变截面区域(图右下)也逐渐贯通，如图12(c)所示。当地震强度达到0.4g时，裂缝贯通区域开始连成一片，由底部向上发展。