非标准抛物线型变截面板簧力学特性解析计算

李雪，周长城*，于曰伟，张云山，欧学昊

(1.山东理工大学 交通与车辆工程学院， 山东 淄博 255000；2.山东汽车弹簧厂淄博有限公司， 山东 淄博 255000)

0 引言

随着汽车轻量化政策的实施，少片变截面钢板弹簧已经广泛应用到汽车上。实际车辆为了满足悬架刚度的设计要求，通常所采用的少片变截面钢板弹簧的抛物线段的坐标原点不在力的作用点上，而是与力的作用点存在一定的坐标偏移量，即少片非标准抛物线型变截面板簧。据所查文献可知，先前对少片变截面钢板弹簧的挠度、刚度及应力的解析计算一直未给出可靠的解析计算公式，均未考虑到抛物线段坐标偏移量及其影响，因此，设计值与实际值存在较大偏差，难以满足少片变截面板簧数字化设计和生产的要求。

目前，国内外大多采用有限元仿真分析法、多体动力学仿真分析法和试验法等对少片变截面钢板弹簧的力学特性进行研究[1-3]。其中，叶南海等[4]通过建立有限元模型，利用ANSYS仿真与实验结果对比，分析了摩擦因数对少片变截面钢板弹簧刚度以及应力的影响；吕新飞和莫立庸等[5]利用Solidworks、ANSYS软件对钢板弹簧进行有限元分析，得到钢板弹簧在不同工作状况下的应力分布状况；唐应时和柴天等[6]利用有限元法对钢板弹簧的预应力进行计算，并通过调整各片板簧的自由弧高和自由曲率半径对各片板簧的预应力进行调整，提高了板簧的使用寿命；文献[7-9]基于解析计算和ANSYS仿真分析，对少片变截面钢板弹簧的刚度及应力特性进行了相关研究；文献[10-13]采用CAE建模仿真和板簧台架试验，对少片变截面钢板弹簧的力学特性进行了对比分析。然而，上述研究方法都是基于少片变截面钢板弹簧的抛物线段的坐标原点在力的作用点的基础上进行的，均没有考虑抛物线段坐标偏移量的影响。对于存在坐标偏移量的非标准抛物线型变截面板簧尚没有准确可靠的刚度以及应力的解析计算方法，不能为少片变截面钢板弹簧的智能化生产提供可靠的理论支撑，也阻碍了钢板弹簧产业的智能化升级进程。

本文根据单片非标准抛物线型变截面板簧的力学模型，利用莫尔积分，建立了变形、刚度的解析计算公式，并分析了坐标偏移量x0对板簧结构及力学特性的影响；在此基础上，根据少片簧与各片板簧之间的刚度与载荷及应力之间的关系，建立了少片非标准抛物线型变截面板簧的变形、刚度和应力的解析计算公式。最后，通过实例，进行了仿真验证和实验验证。

1 单片非标准抛物线型变截面板簧的刚度及应力的解析计算

1.1 单片非标准抛物线型变截面板簧的结构以及力学模型

将单片非标准抛物线型变截面板簧的一半等效为悬臂梁，在卷耳中心位置施加垂向载荷，与车轴固定连接的位置为固定端约束，忽略卷耳部分，端部的起始点为非标准抛物线型变截面板簧的卷耳中心。由于板簧的端部厚度变化较小，将其近似看作等厚的平直段，端部的有效长度取卷耳中心到抛物线端部的跨度。由于钢板弹簧中间平直段受U型螺栓夹紧的影响，在计算时，取其长度的一半作为有效长度。基于以上假设，建立单片非标准抛物线型变截面板簧一半对称结构的力学模型，如图1所示。

图1 单片非标准抛物线型变截面板簧一半对称结构的力学模型Fig.1 Half of the mechanical model of the symmetrical structure of the single-chip nonstandard parabolic tapered leaf spring

图1中，板簧的根部到自由端的总长度为L，端部平直段的长度为l1，板簧抛物线段根部到自由端的长度为l2，根部平直段长度为l3，l3的长度取决于车轴的安装尺寸；根部平直段的厚度为h2，端部平直段的厚度为h1，抛物线段厚度比为β，其中β=h1/h2；板簧的宽度为b，弹性模量为E。在板簧的自由端施加集中力F，其大小为整簧承受载荷的一半。

① 抛物线段在理论坐标下的坐标偏移量x0

以板簧的自由端O为坐标原点建立坐标系，抛物线段的理论坐标原点为OT，板簧自由端O与抛物线段的理论坐标原点OT之间的距离为抛物线段的坐标偏移量x0。利用在理论坐标系OT下，抛物线段的根部和端部到理论坐标原点的距离l2+x0和l1+x0之间的关系，可得抛物线段的坐标偏移量x0为

(1)

② 抛物线段在原坐标x位置的厚度h(x)

根据抛物线段根部厚度h2、抛物线段的根部到板簧自由端的长度l2、端部平直段的长度l1及坐标偏移量x0，可建立板簧抛物线段在原坐标下的厚度h(x)表达式，即

(2)

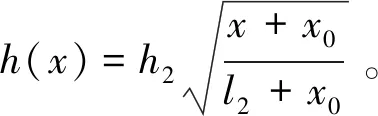
1.2 单片非标准抛物线型变截面板簧变形及刚度的解析计算

根据单片非标准抛物线型变截面板簧一半对称结构的力学模型，利用莫尔积分可知，板簧在端部集中力F作用下的端部挠度可表示为

(3)

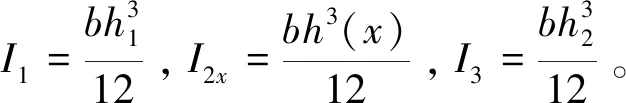
对式(3)进行积分运算并整理，可得单片非标准抛物线型变截面板簧端部挠度的解析计算式为

(4)

式中，GD为单片非标准抛物线型变截面板簧的端部挠度系数，且

由式(4)可知单片非标准抛物线型变截面板簧的刚度为

(5)

1.3 单片非标准抛物线型变截面板簧应力的解析计算

根据图1所示的单片非标准抛物线型变截面板簧一半对称结构的力学模型，当板簧端部受到集中力作用时，由材料力学可知，板簧在任意x位置处的应力为

(6)

式中，M(x)为板簧任意x位置处承受的弯矩，且M(x)=Fx；W(x)为任意x位置处的抗弯截面系数，W(x)=bh2(x)/6，h(x)为不同位置x处板簧的厚度。

因此，整理式(6)，可得单片非标准抛物线型变截面板簧在任意x位置处的应力解析计算式为

(7)

2 单片非标准抛物线型变截面板簧抛物线段坐标偏移量x0的影响分析

由式(2)、式(4)、式(5)和式(7)可知，抛物线段的坐标偏移量对板簧的厚度、刚度、变形及应力有重要影响。以某单片变截面板簧为例，分析抛物线段坐标偏移量x0对板簧自身结构和力学特性的影响规律。其原始结构参数为：板簧宽度b=80 mm，作用长度L=550 mm，根部平直段的长度l3=50 mm，抛物线段的根部至自由端的长度l2=500 mm，板簧的根部厚度为h2=20 mm，抛物线段的厚度比为β=0.4。板簧端部所受集中力F=1 000 N，弹性模量E=206 GPa。

2.1 坐标偏移量x0对抛物线段厚度的影响分析

根据单片非标准抛物线型变截面板簧的厚度表达式，绘制不同坐标偏移量x0下板簧厚度随位置的变化规律曲线，如图2所示。

图2 不同坐标偏移量x0下板簧厚度的变化规律曲线Fig.2 Thickness curve of the leaf spring under different coordinate offsets x0

分析图2可知，当作用长度L，宽度b，根部平直段长度l3以及根部厚度h2确定时，坐标偏移量x0对于板簧的根部平直段和端部平直段的厚度没有影响；当x0越大，同一位置处，板簧抛物线段的厚度越大，其中x0对于近端部的抛物线段的厚度影响最大；除此之外，随x0增大板簧端部区间长度减小，抛物线段区间长度增大。

2.2 坐标偏移量x0对板簧刚度和挠度的影响分析

当坐标偏移量x0在一定范围内变化时，其对板簧刚度和板簧挠度均产生一定影响。根据单片非标准抛物线型变截面板簧刚度、挠度的解析计算式，分别绘制板簧刚度、挠度随坐标偏移量x0的变化规律曲线，分别如图3、图4所示。

据图3、图4可知，当其他参数相同时，坐标偏移量x0对板簧的刚度和挠度均有重要影响。其中，板簧的刚度随着坐标偏移量x0的增大而增大，且整体呈现非线性变化；板簧的挠度随着坐标偏移量x0的增大而减小，整体也呈现非线性变化。

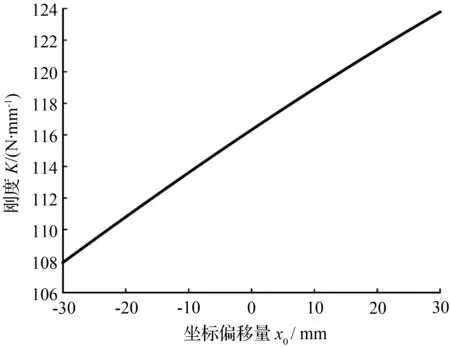
图3 板簧刚度随坐标偏移量x0的变化规律曲线Fig.3 Stiffness curve of the leaf spring with coordinate offset x0

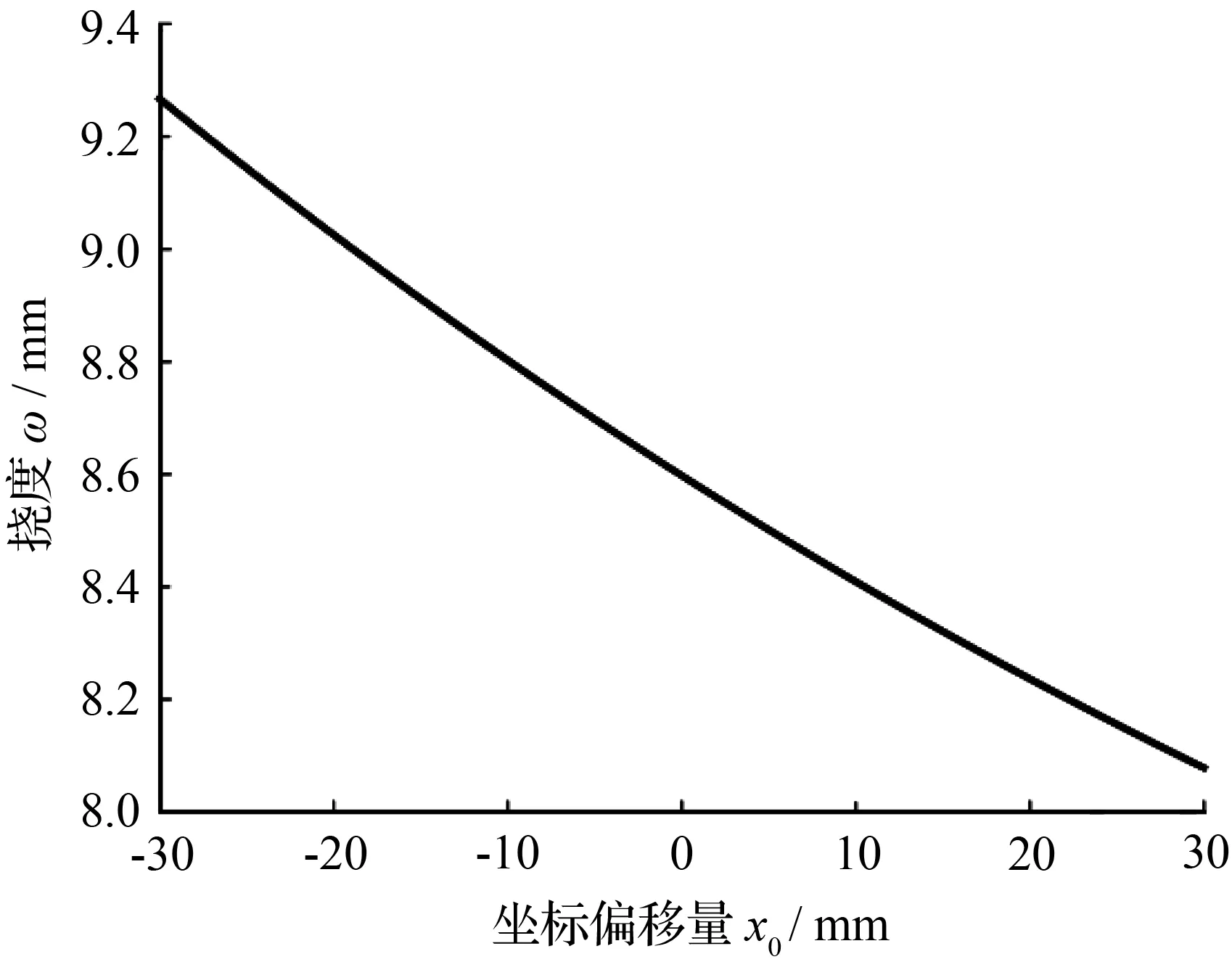
图4 板簧挠度随坐标偏移量x0的变化规律曲线Fig.4 Deflection curve ofthe leaf spring with coordinate offset x0

2.3 坐标偏移量x0对板簧应力特性的影响分析

根据单片非标准抛物线型变截面板簧的应力计算式，利用Matlab软件绘制不同坐标偏移量x0下应力随位置的变化规律曲线，如图5所示。

由图5可知，单片非标准抛物线型变截面板簧的应力，在其端部平直段和根部平直段，随长度x的增大呈线性增大趋势；当x0=0时，板簧抛物线段呈等应力变化，最大应力出现在在板簧根部；当x0>0时，抛物线段不再呈现等应力变化，而是随长度x的增大而增大且总体上呈现非线性变化，且随着x0增大，其端部平直段区间长度减小，抛物线段区间长度增加，最大应力出现在板簧根部。而当x0<0时，抛物线段的应力，随长度x的增大而减小且总体上呈现非线性变化，且随着x0增大，其端部平直段区间长度减小，抛物线段区间长度增加，最大应力出现在板簧的根部或者抛物线段的端部处，这与x0的取值有关。

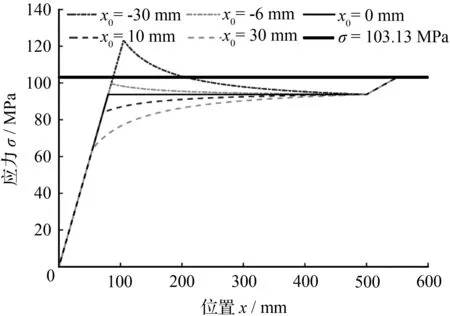
图5 不同坐标偏移量x0下应力随位置的变化规律曲线Fig.5 Stress curve with position under different coordinate offset x0

根据其应力计算式，绘制抛物线段和根部平直段的最大应力随坐标偏移量x0的变化规律曲线，如图6所示，其中，虚线代表板簧根部平直段的最大应力，实线代表板簧抛物线段的最大应力。

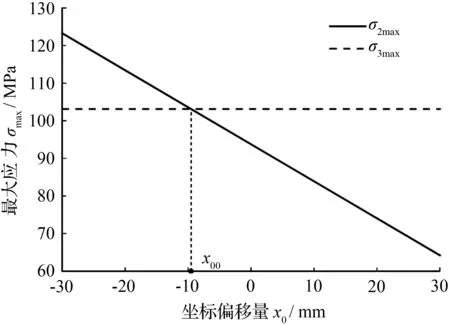
图6 板簧的最大应力随坐标偏移量x0的变化规律曲线

根据图6可知，板簧抛物线段的最大应力随着x0的增大而减小，且整体呈现线性变化。当板簧抛物线段最大应力与根部的最大应力相等，即σ2max=σ3max时，此时抛物线段的坐标偏移量为

因此，当x0x00时，其最大应力出现在板簧根部，即x=L处；当坐标偏移量x0=x00时，非标准抛物线型变截面板簧的抛物线段与根部平直段的最大应力相等，此时x=l1、x=L处均为该板簧的最大应力位置。

3 少片非标准抛物线型变截面板簧刚度及应力的解析计算

3.1 少片非标准抛物线型变截面板簧刚度及挠度的解析计算

少片非标准抛物线型变截面板簧是由单片非标准抛物线型变截面板簧叠加而成，其一半对称结构的力学模型如图7所示。板簧的片数为n，一般2≤n≤5，板簧的宽度为b，弹性模量为E，各片非标准抛物线型变截面板簧的端部厚度为hi1，根部厚度为hi2，抛物线段的厚度比βi=hi1/hi2板簧的根部到自由端的总长度为L。端部平直段的长度为li1，l2为抛物线段根部到自由端的长度，l3为根部平直段的长度，各片板簧抛物线段的坐标偏移量为xi0=(l2βi2-li1)/(1-βi2)，板簧端点集中力为F。

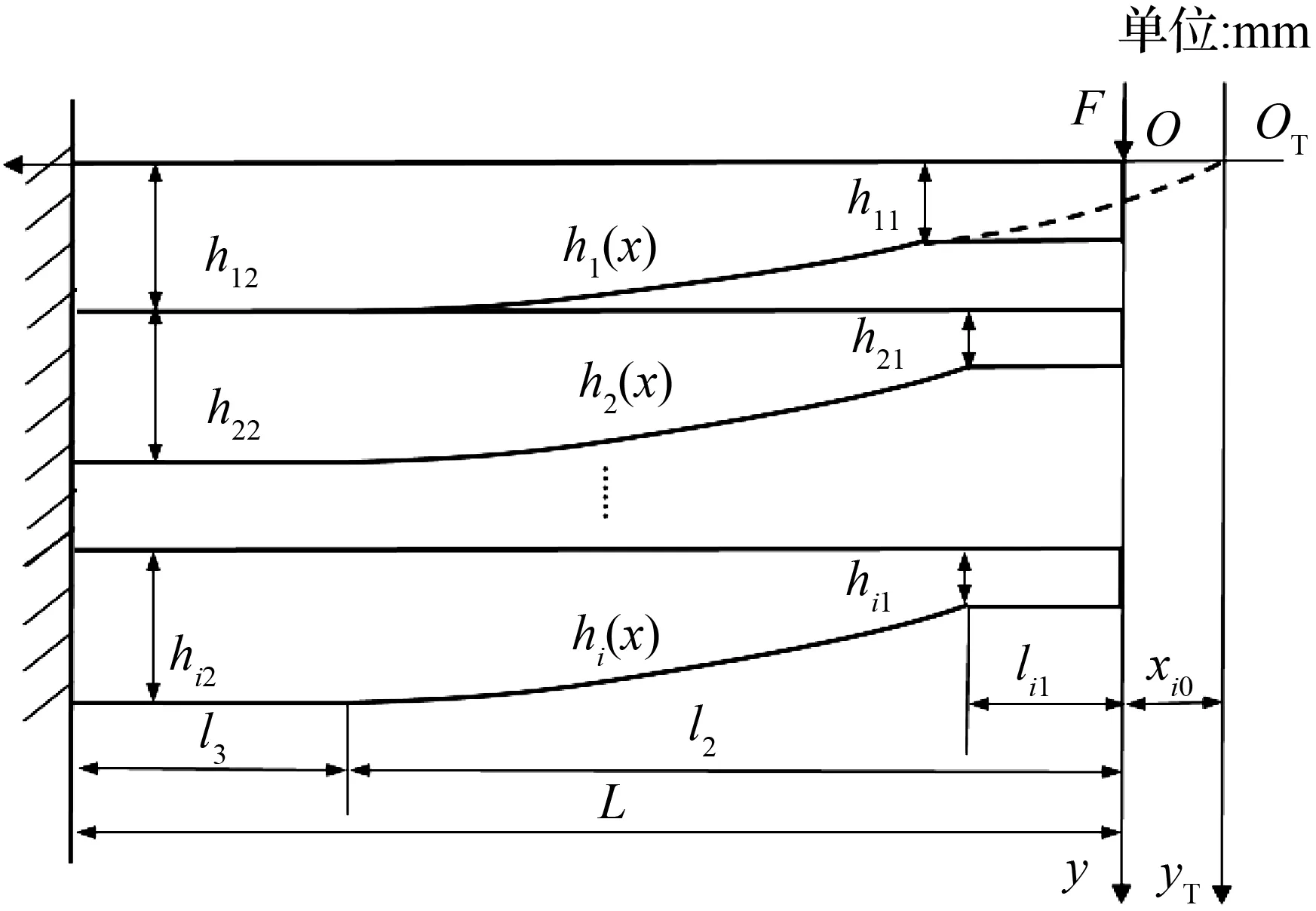
图7 少片非标准抛物线型变截面板簧一半对称结构的力学模型Fig.7 Half of the mechanical model of the symmetrical structure of the few-chip nonstandard parabolic tapered leaf spring

由式(5)可知，少片非标准抛物线型变截面板簧各片的刚度为

(8)

式中，GDi为各片板簧的端部挠度系数，即

因此，少片非标准抛物线型变截面板簧的总刚度可表示为

(9)

根据挠度与刚度的关系式，可求得少片非标准抛物线型变截面板簧端部的变形为

(10)

由各片板簧承担的载荷之和等于总载荷，端部变形等于总变形，易求得各片板簧承担的载荷为

(11)

3.2 少片非标准抛物线型变截面板簧应力的解析计算

根据少片非标准抛物线型变截面板簧各片的刚度和载荷之间关系，由式(7)和式(11)，可得各片板簧任意x位置处的应力解析计算式为

(12)

4 实例计算与ANSYS仿真验证

4.1 实例参数

已知某款车型前悬架板簧的片数为n=3，板簧宽度b=80 mm，弹性模量E=206 GPa。板簧的作用长度L=550 mm，根部平直段的长度l3=50 mm，抛物线段的根部至自由端的长度l2=500 mm，端部平直段的长度分别为l11=110 mm、l21=l31=90 mm。板簧根部平直段的厚度为hi2=15 mm，端部平直段的厚度分别为h11=7.5 mm、h21=h31=6 mm；各片板簧抛物线段的厚度比分别为β1=7.5/15=0.5、β2=β3=6/15=0.4；板簧端部所受的集中载荷为F=8 250 N。

4.2 实例计算

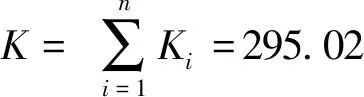
图8 第1片板簧应力变化曲线图Fig.8 Stress curve of the first leaf spring

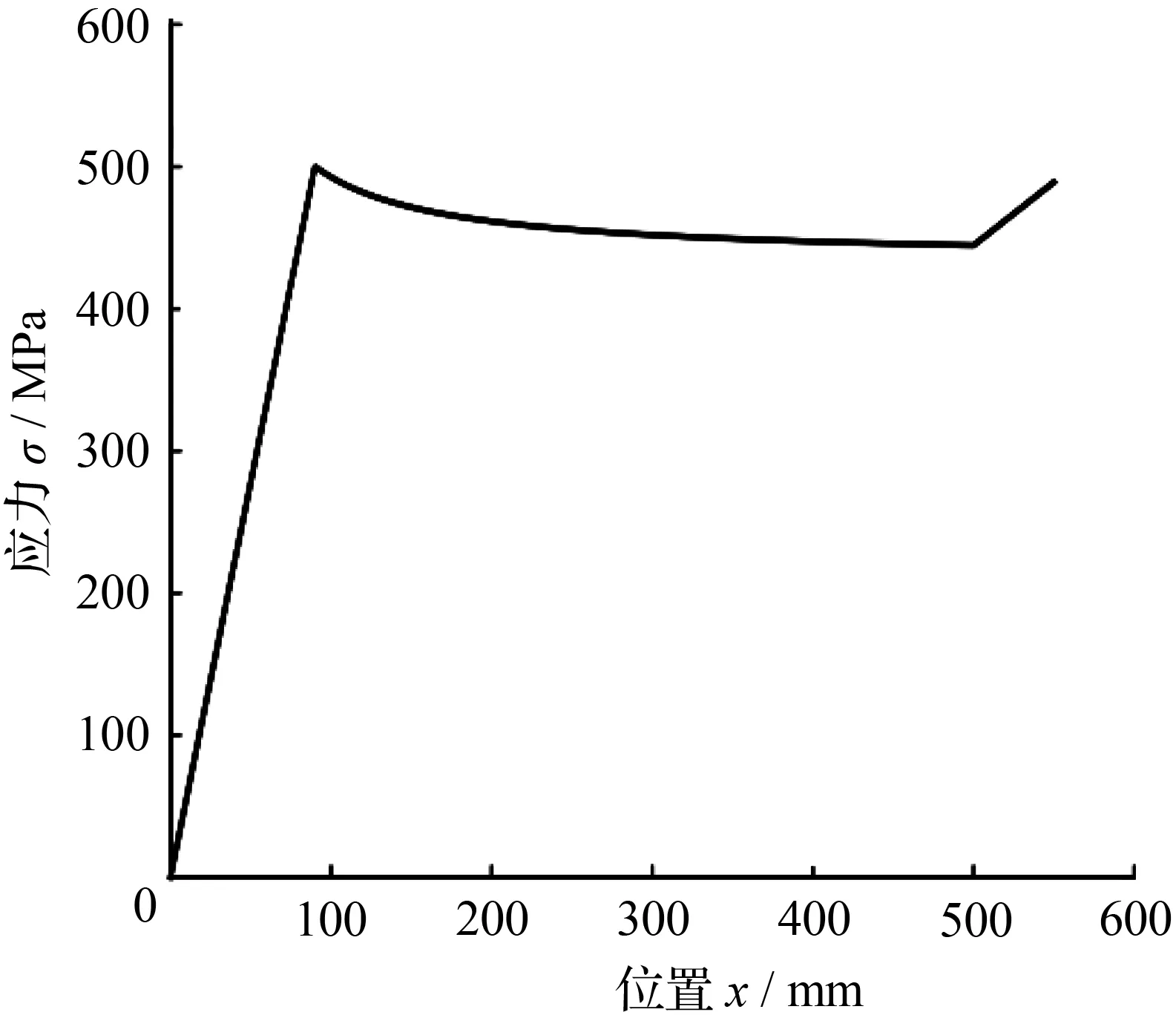
图9 第2、3片板簧应力变化曲线图Fig.9 Stress curve of the second, third leaf spring

由图8可知，首片板簧的最大应力出现在根部，即首片板簧在车桥上的固定位置，其最大应力为546.99 MPa。由图9可知，第2、3片板簧的最大应力应力出现在x=90 mm处，即抛物线段的端部，且其最大应力为510 MPa。

4.3 ANSYS仿真验证

根据计算实例中板簧的结构参数、弹性模量和载荷，利用ANSYS软件建立其三维模型并对其变形和最大应力进行仿真计算，所得到的少片非标准抛物线型变截面板簧的变形仿真云图和各片板簧的应力仿真云图，分别如图10、图11所示。

图10 少片非标准抛物线型变截面板簧的变形仿真云图Fig.10 Deflection simulation cloud diagram of the few-chip nonstandard parabolic tapered leaf spring

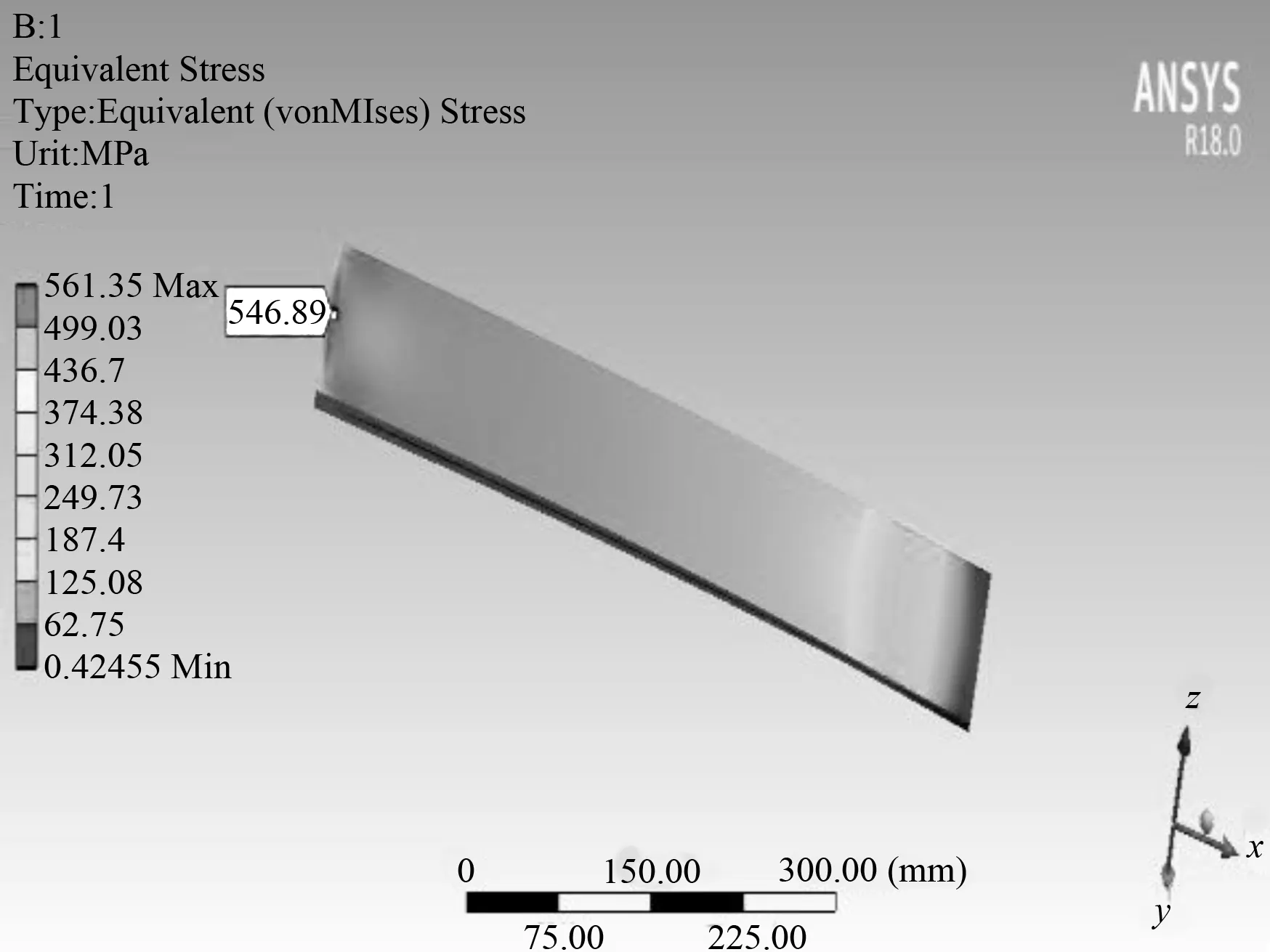
(a) 第1片板簧

由图10、图11可知，仿真得到的少片簧的最大挠度值为55.55 mm，其刚度值为297.02 N/mm；首片板簧的最大应力为546.89 MPa，第2、3片板簧的最大应力为510 MPa，与解析计算值的相对偏差分别为0.7 %，0.7 %，2.3 %和1.9 %。结果表明，所建立的少片非标准抛物线型变截面板簧的挠度、刚度及应力解析计算公式及方法是正确的。

4.4 试验验证

为进一步验证所建立的非标准抛物线型变截面板簧的挠度及刚度解析计算方法的可信性，进行了试验验证。所用设备为济南时代试金集团生产的TYE-W400I微机控制液压式弹簧压力试验机，如图12所示。该设备可自动进行试验数据的采集与处理，并通过微机显示屏直接输出板簧试验力、板簧变形量及板簧特性曲线。利用该设备对板簧进行加载-卸载挠度特性试验。其中板簧片间已做好润滑，板簧已用骑马螺栓夹紧，所加载的最大载荷为10 500 N。对该板簧样机加载和卸载的挠度数据进行拟合处理，得到该少片非标准抛物线型变截面板簧的实验刚度值为283.1 N/mm，与解析计算值相比，相对偏差为4.2 %。结果进一步表明所建立的少片非标准抛物线型变截面板簧的挠度及刚度的解析计算公式及方法是可靠的。

图12 少片簧加载-卸载试验平台Fig 12 Loading-unloading test platform of the few-chip leaf spring

5 结语

本文通过对非标准抛物线型变截面板簧力学特性的理论分析、实例计算及仿真和实验验证，可知：

① 根据非标准抛物线型变截面板簧的结构参数，可对板簧抛物线段的坐标偏移量x0及不同位置x处的板簧厚度h(x)进行解析计算。

② 根据非标准抛物线型变截面板簧的力学模型，利用莫尔积分，可建立非标准抛物线型变截面板簧的挠度和刚度的解析计算式，可实现对其挠度和刚度进行解析计算。

③ 根据少片非标准抛物线型变截面板簧的各片端部所受载荷与刚度的关系，建立少片非标准抛物线型变截面板簧在任意位置处的应力计算公式。

④ 当板簧跨度、宽度、根部平直段长度以及根部厚度确定时，不同抛物线段坐标偏移量x0，对板簧抛物线段在任意x位置处的厚度、刚度和应力均有重要影响。

⑤ 仿真结果表明，少片非标准抛物线型变截面板簧的变形解析计算值及最大应力解析计算值与其相对应的仿真值均相吻合，相对偏差均在2.3 %以内。所建立少片非标准抛物线型变截面板簧的变形及应力计算公式是准确的。少片簧的刚度测试结果与解析值吻合，相对偏差在4.2 %以内。对比结果进一步表明，所建立的挠度和刚度的解析计算方法是可靠的。

本文所建立的非标准抛物线型变截面板簧力学特性的解析计算方法，可得到准确的刚度计算值和板簧任意位置处的应力值，为少片变截面钢板弹簧的设计、刚度匹配和应力校核等提供了可靠的技术基础，也为悬架系统的零部件现代化设计及特性仿真提供了理论参考。