数学问题链设计“三步曲”*——以“基本不等式”为例

(象山县第二中学,浙江 象山 315731)

“问题链”是教师为了实现一定的教学目标，根据学生的已有知识或经验，针对学生学习过程中将要产生或可能产生的困惑，将教材知识转换成为层次鲜明、具有系统性的一连串的教学问题；是一组有中心、有序列、相对独立而又相互关联的问题[1].“问题链”教学具有一般传统教学无可比拟的优越性：一方面，它为学生提供了数学学习的骨架，使学生能够经问题链获得较高水平的数学知识；另一方面，问题链中问题间的跨度又为学生的高水平思维提供了无限的可能[2].问题链是知识探究的程序链，更是学生思维的触发器，显然，决定问题链教学成败的关键是“问题链”的设计.下面，笔者就以“基本不等式”一课为例，谈谈问题链设计的“三步曲”.

1 深入解读教材，探寻“联结点”

构建问题链的第一步是寻找知识的“联结点”，然后按照一定的教学逻辑把各个“联结点”串联起来，从而实现教学过程的协调统一与有序转化，这也是“问题”能够“成链”的关键.那么“联结点”如何找呢？这就需要教师深入解读教材.对于“基本不等式”这节课，我们需要思考以下两个问题.

1.1 为什么学习基本不等式

很多教师会把学习基本不等式的目的归结为“获得求最值问题的有利工具”，但这只是说明了基本不等式很有用，却不是学习它的直接理由.学习基本不等式应该立足“不等式”的整个章节，从知识系统的角度来分析.《普通高中数学课程标准(2017年版)》指出，学习“不等式”的目的是让学生体会“不等式是刻画现实世界的重要模型”.教材从“不等关系”入手明确不等式的表示，通过“不等式的8个基本性质”明确不等式的逻辑关系与运算法则，通过解“一元二次不等式”与“绝对值不等式”获得运算经验，至此不等式的一般理论雏形基本建立.于是，就开始学习不等式的具体模型——基本不等式.其实，高中阶段所有的数学内容都是按照“概念—表示—运算—逻辑关系—具体模型”的方式展开，这符合认识数学对象的一般套路.因此，学习基本不等式的目的就是认识一个具体的不等式模型，从而进一步体会不等式是刻画现实世界的重要模型.

1.2 为什么基本不等式能被称为“基本”

2 拓展联结点，确定“问题主干”

联结点是问题链的“根基”，通过拓展联结点来确定“问题主干”是问题链设计的第二步.通常一个联结点可以沿着不同的方向进行拓展，每个方向都可以确定一个相对独立的问题主干，问题链就是依附于这些“问题主干”而生成的.

基本不等式这节课的联结点落在“基本”上面，拓展的关键就是如何揭示“基本”的内涵.“基本”按照字面的理解就是“基础+本质”.“基础”的东西往往意味着“容易”，因此，可以通过从不同的视角来解释基本不等式的“容易”，从而来揭示基本不等式的“本质”.按照这个思路，本节课的问题主干可以从以下几个方面进行确定.

2.1 因基本而“容易发现”

作为“基本”的数学模型，基本不等式的“发现”途径有很多.可以从“几何图形”中发现，人教A版教材就是先从“弦图”中抽象出“重要不等式”，然后通过“降维”得到“基本不等式”.如果能够借助“圆内接直角三角形的中线与高”这个图形，基本不等式的发现就会容易得多.当然，还可以从更多的“几何图形”中发现基本不等式.基本不等式还可以从“生活”中发现，苏教版教材就是从“失衡天平称重物”这一生活经验中发现基本不等式的.基本不等式还可以从“物理运动”中发现、从数列中发现，在此笔者就不再赘述.总之，由于“基本”，基本不等式的发现就很“容易”.因此，问题链设计的一个主干问题就是如何使学生“容易发现”基本不等式.

2.2 因基本而“容易证明”

基本不等式的证明也很“容易”.“作差法比较”是学生最容易想到的方法，人教A版教材采用的是“分析法”.其实，还可以利用方程性质、函数最值、向量数量积、点到直线的距离等技巧进行证明，方法不下10余种.由于“基本”，基本不等式的证明视角很多，方法很多，学生很“容易证明”.因此，问题链设计的另一个主干问题就是如何让学生感受基本不等式证明之“容易”.

2.3 因基本而“容易推广”

这个不等式链分别揭示了4个平均数“调和平均数、几何平均数、算术平均数、均方根平均数”的大小关系.不仅如此，基本不等式还可以拓展到三维、n维，还可以生成其他一系列的齐次不等式.因此，让学生经历基本不等式的变形推广过程是问题链设计的另一个主干.

3 细化主干问题，生成“问题链”

问题主干的不断细化与延伸就可以生成问题链，若干个主干就有若干条问题链，若干条问题链就构成了整节课的问题系统.“问题链”中的问题要求按照一定的教学逻辑进行串联，层层递进，环环相扣，步步深入，由此及彼[3].一条“问题链”就是一条知识线、思维线，不断地驱动着学生的思考与学习的进程.

3.1 如何“发现”基本不等式

相对于“从生活中发现基本不等式”与“从物理中发现基本不等式”，从“几何图形”中发现基本不等式不仅比较直观，而且还可以实现“不证自明”的效果.因此，第一个主干问题应该回答的是：

主干问题1如何从几何图形中发现基本不等式?

图1 图2

问题1-1我们知道不等关系与不等式在生活与数学中无处不在，如图1所示，比较图中的线段长度，说说存在着哪些明确的不等关系？

问题1-2设线段AD=a，DB=b，你能得到怎样的不等式？

问题1-3如图2所示，比较图形中的面积，你能发现什么不等式关系？

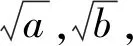
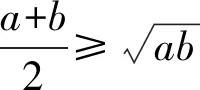
图3

意图通过图形的直观呈现，引导学生经历从定性到定量、从一维到二维、从浅层到深度的思维过程，感受基本不等式的几何背景，感受基本不等式是“容易发现”的，体会基本不等式是刻画现实世界的“基本”模型.

3.2 如何“证明”基本不等式

主干问题2证明基本不等式的方法有哪些?

问题2-1证明不等式常用的方法有哪些？

问题2-2如何证明基本不等式？

问题2-3分析基本不等式的结构，还有其他证明方法吗？

意图引导学生用最容易想到的方法——“作差比较法”去证明不等式，在已有证明的基础上，经历观察、分析、构造的思维过程，进一步探索比较巧妙的证明方法，从而进一步感受基本不等式的“基本”.

基本不等式有很多巧妙的证明，例如可以用函数的视角去证明：

不妨设a≥b，令m=a-b，则m≥0，即b=a-m，从而

即

当然，这种方法学生不容易想到，教师可以通过设计相应的“问题链”启发学生.

3.3 如何“推广”基本不等式

主干问题3基本不等式能够推广为哪些不等式？

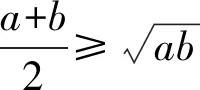
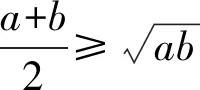
问题3-3已知不等式通过降维、换元、升维等方法，可以获得新的不等式.从基本不等式出发，你能够获得哪些新的不等式呢？你能够证明这些不等式吗？

意图通过前面两个问题的解决，学生可以获得不等式推广的一般经验，为后续问题的解决做好必要的思维铺垫.问题3-3是一个开放性的问题，能够启迪学生的思维，深入体会基本不等式的“基本”属性.

问题链就是问题研究的支架与框架，它促使学生有序、有向、有度地进行数学学习，从而有效地避免了课堂教学中存在的“琐碎问”“满堂问”“满堂灌”等弊端，学生的认知结构也在不断地“发现问题—解决问题—再发现问题”的过程中走向完善.