一种新型短波矢量阻抗检测设计与实现*

邹晶晶

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引 言

在短波发信机种，天线调谐器作为功放与天线间的匹配设备，通过检测天线负载的阻抗调整匹配网络参数，使得功放与天线间阻抗得到良好匹配，提高短波发射系统的功率传输效率，避免功放与天线间因阻抗失配导致反射功率过大而损坏发射系统。矢量阻抗检测模块是天线调谐器的关键模块，是天调执行调谐算法的基础，其检测精度直接决定了天调的调谐精度。高精度矢量阻抗检测技术可在短波全频段提供准确的负载阻抗检测，是实现快速、高精度天调调谐器的关键技术[1]。短波频段内矢量阻抗检测技术通常存在两种电路处理构架：一是变频处理构架，二是射频直采处理构架。

1 变频构架矢量阻抗检测

1.1 检测原理

变频处理构架的工作原理[2]如下：射频信号下变频后，通过ADC采样低频信号，获取与负载相关的电压、电流矢量信号，基于矢量阻抗定义式

计算求得负载阻抗。该种方式直观，且阻抗幅角即是电压、电流信号的相位差。电压、电流矢量信号获取方式一般采用耦合器完成，变压器耦合射频电压信号，电流耦合器耦合通过负载的电流信号，为降低耦合器本身对负载阻抗的影响，一般耦合系数相对较小，耦合信号需通过放大后再进行后续下变频、滤波等处理得到中频信号，中频信号经放大、滤波处理后进行低频采样，在数字域中提取低频采样信号的幅度、相位信息，计算得到阻抗值，其处理构架如图1所示。

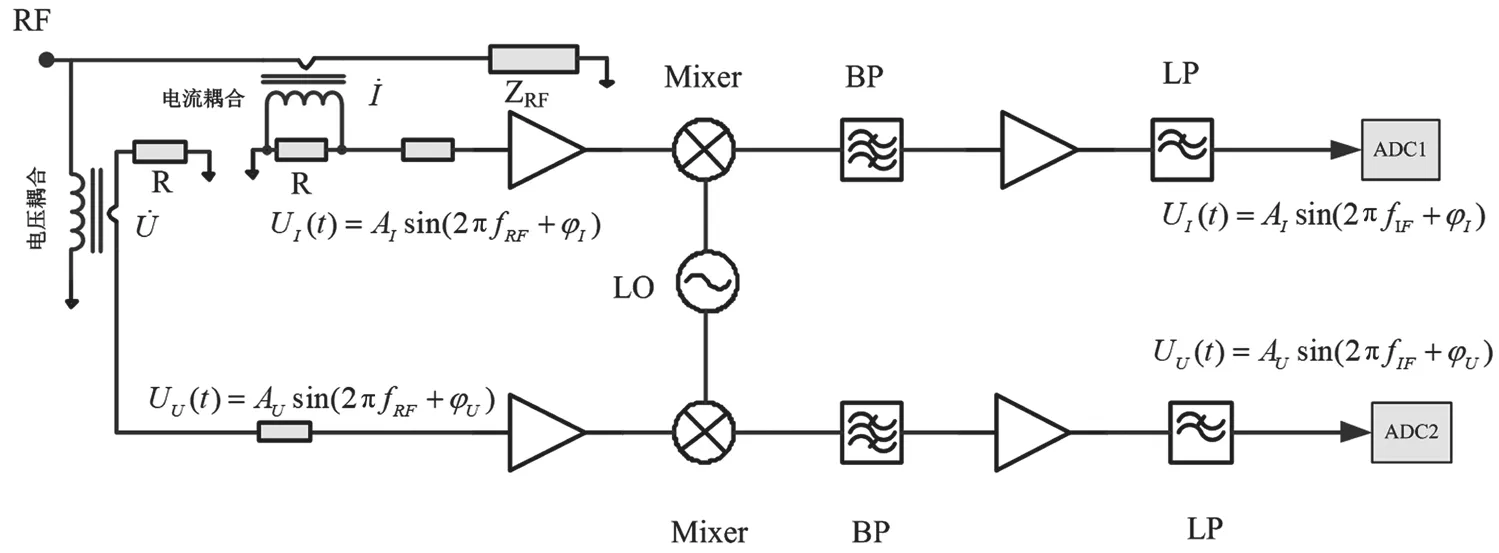
图1 变频构架矢量阻抗检测原理

1.2 矢量阻抗计算方法

耦合器耦合与负载相关的电压、电流射频信号：

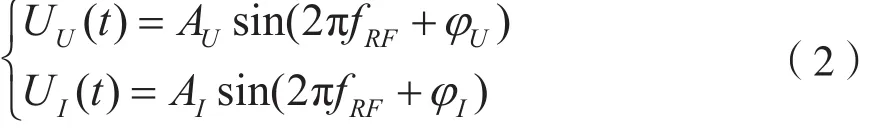
在射频耦合器中，电压耦合器为变压器，电流耦合器为线圈互感器[3]，其耦合后的电压、电流与调谐信号的关系可表示为：

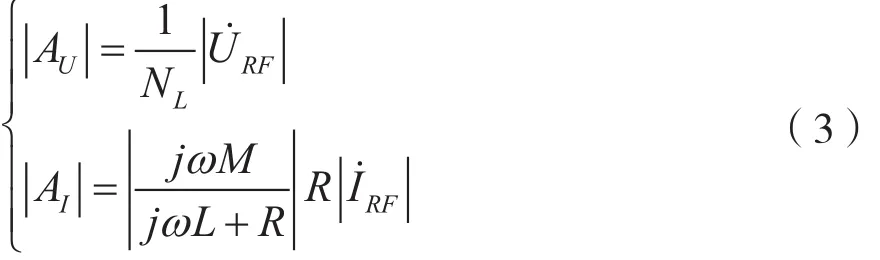
式中NL为耦合器线圈匝数比，M为电流耦合器的互感，L为电流耦合器的自感，且L/M=NL，R为耦合器取样电阻。

经混频器下变频后，得到中频电流电压采样信号：

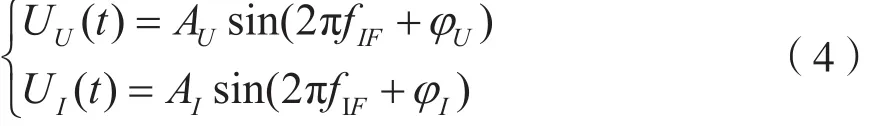
A/D采样后的离散样点信号可表示为：

计算离散信号的幅值：

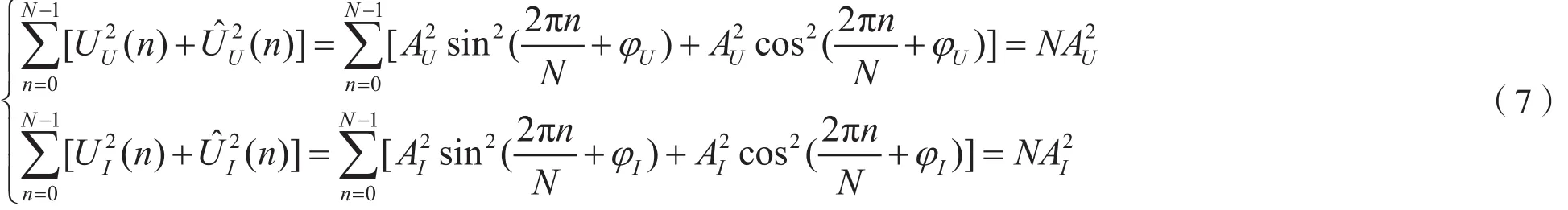
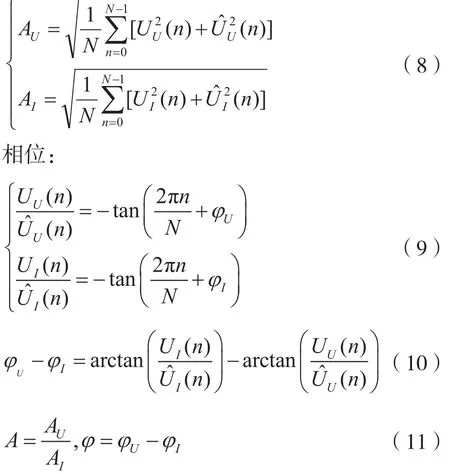
最后得到阻抗：

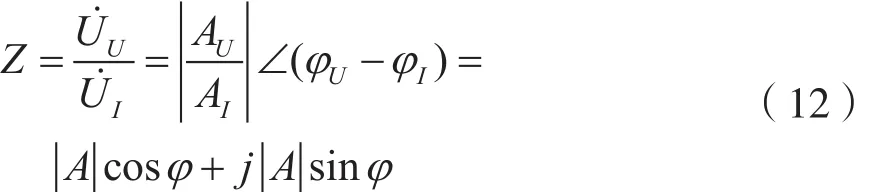
检测到的实际矢量阻抗为：

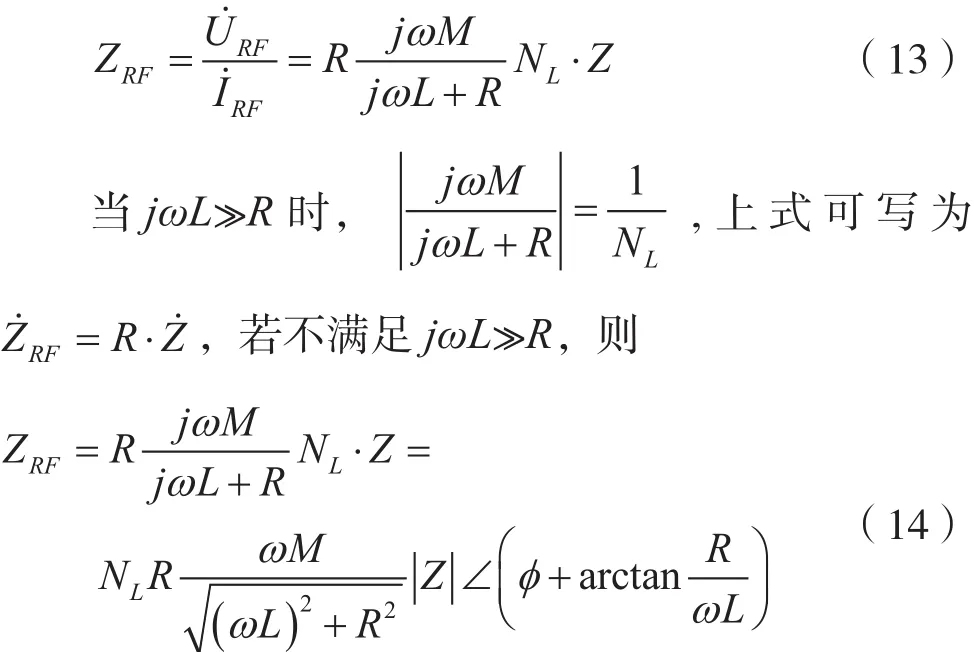
变频构架下的矢量阻抗检测处理电路较为复杂，中频采样后进行数据处理计算负载阻抗，数据处理中提取电流、电压信号幅度、相位特性需进行希尔伯特变换，算法复杂度高。此外，由于工程实现中，耦合器存在固有频率特性，两路射频处理电路处理的不平衡性，对阻抗检测误差造成较大影响（误差在5%～10%）。此种检测方式中感性耦合器尺寸大、电路复杂、功耗高，在体积、功耗受限的设备中难以实现。

2 射频直采构架矢量阻抗检测

2.1 检测特点

针对变频处理构架下短波矢量阻抗检测器电路复杂、体积大、功耗高、数据处理复杂度高等问题，本文在电路处理构架、数据处理算法两方面提出改进，设计了一种短波射频直采桥式矢量阻抗检测（以下简称“桥式检测”）方法。与传统方法相比，表征负载阻抗的电压、电流信号不经过下变频处理，直接进入高速ADC进行采样，在数字域进行数据处理得到负载阻抗。该种检测方式下，不存在耦合器、下变频等处理电路，电路复杂度降低，可实现低功耗、小体积设计，与变频构架检测电路相比，具有如下特点：

（1）硬件电路实现上，基于射频直采电路构架，无感性耦合器、混频器、滤波器、放大器等部件，缩小检测电路模块体积、功耗，降低外围电路引入的检测误差；

（2）采用短波频率特性较好的纯电阻网络代替电压、电流耦合器，降低耦合器频率特性造成的检测误差；

（3）在数据处理算法上，直接对采样数据处理，无需对数据进行下变频、希尔伯特变换等处理，处理算法简洁、高效。

2.2 检测原理

桥式检测电路构架如图2所示。

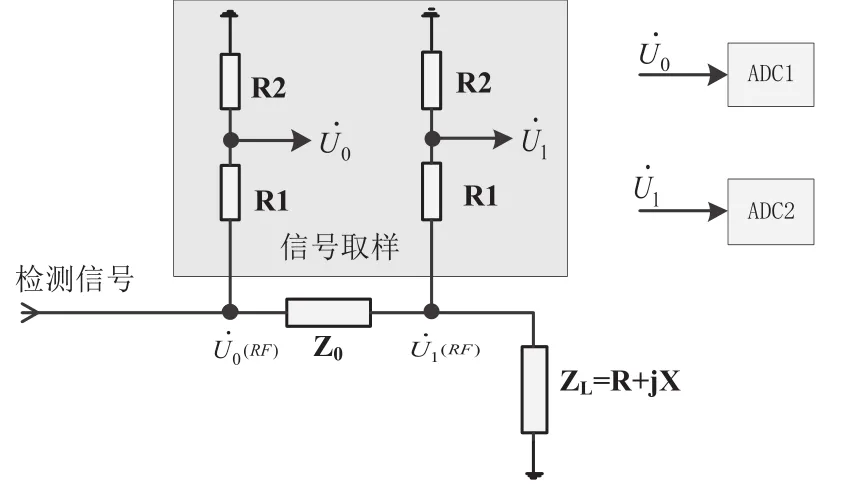
图2 桥式检测电路构架

检测电路由参考桥接阻抗Z0及信号取样电路构成，对于任意负载Z=R+jX，可假设流过Z0的电流也流入了负载ZL，有如下公式成立：

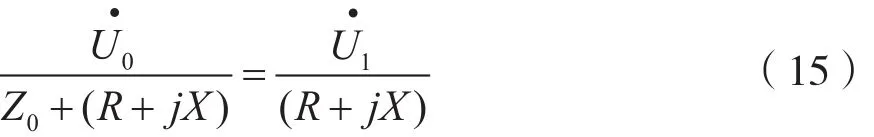
其中，

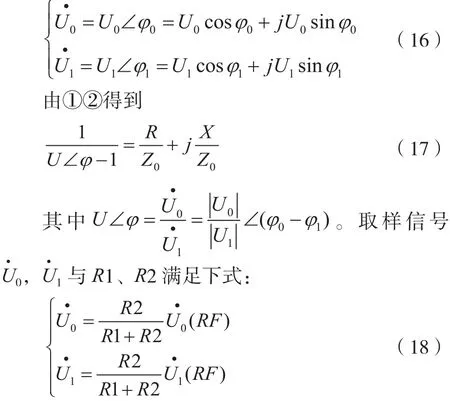
信号取样电路中R1、R2为纯阻，当R1、R2远大于ZL时，取样后不影响检测信号在参考桥接阻抗Z0两端的相位，只在幅度上等比例缩小，因此，矢量电压之比可用表示为：

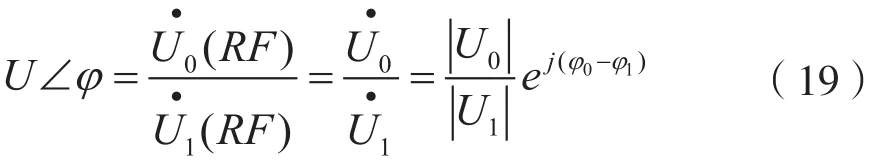
其中|U0|、|U1|取样信号幅度，φ0-φ1为相位差。对进行直接采样，通过对样点数据的分析处理，提取相位、幅度信息，可计算得到负载阻抗ZL。

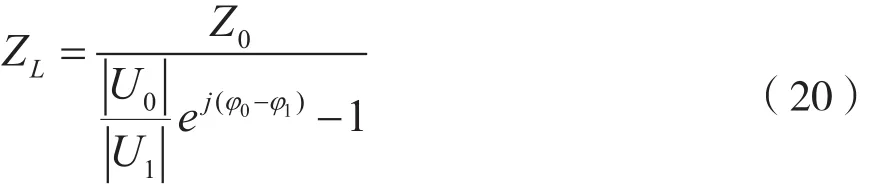
由此可见，只需求得检测器Z0前后两端的电压向量，即可得到负载ZL。由于①基于流过Z0的电流也流过ZL，这就需要U1支路的引入不影响ZL的值，即U1支路的阻抗远大于负载支路阻抗。

基于样点数据提取两路信号的幅度、相位信息，带入阻抗计算公式⑥得到负载阻抗值。两路采样信号的幅度可由样点数据计算均方根值得到。信号的相位差分两步进行：第一步求相位差绝对值|φ0-φ1|，第二步求判定U0与U1的超前/滞后关系，确定相位差符号。

|φ0-φ1|的求取基于相关分析法。两路采样信号U0(n)与U1(n)可表示为：

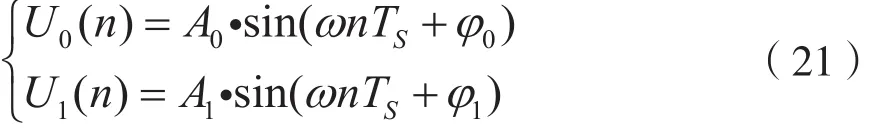
其中TS为采样周期。其互相关函数

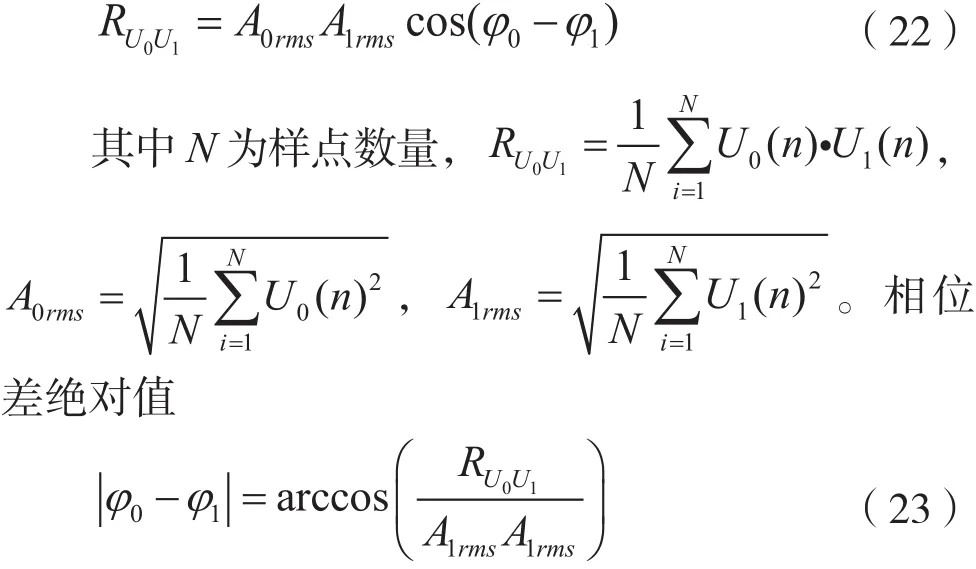
相位超前滞后的判定基于统计思想，通过判定两路信号极大值出现的时刻，并统计极大值出现时刻，根据统计结果，判定相位差符号。极大值的定义为：在一段连续采样的区间内，若区间中某个点的值大于区间内前序所有点的值，同时大于区间内后序所有点的值，则此点称为序列的一个极大值点。考虑到采样的误差，区间的长度随调谐信号的频率而发生变化。比较极大值点所处的时间轴（采样后的序列ID），先出现极大值的点定义为序列的相位超前点，后出现极大值的点定义为序列相位滞后点，若极大值的ID相同，则丢弃。统计相位超前、滞后点数，若相位超前的点数多于相位滞后的点数，则判定为相位超前，相位差符号为“+”；若相位滞后的点数多于相位超前的点数，则判定为相位滞后，相位差符号为“-”。

以下举例说明相位计算过程。如图3为检测信号为2 MHz、样点数位128时数据。

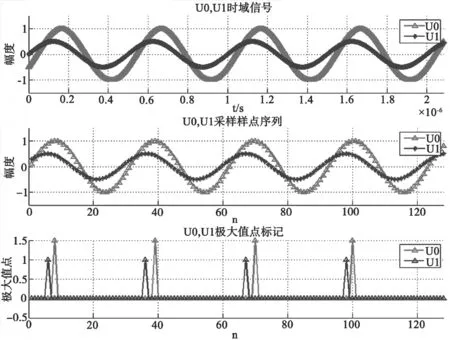
图3 相位计算举例

图3（上）位时域信号，图3（中）为样点数据，图3（下）两路信号极大值（非0点）序列。通过式⑨计算可得相位差绝对值

U0极大值点与U1极大值点数相同，且均滞后于U1，相位差判定为滞后，相位差符号位“-”，因此，最终相位差

3 桥式检测器仿真

3.1 检测精度仿真

借助Multisim仿真软件，提取示波器时域样点数据，样点速率为65 MHz，基于采样点计算负载阻抗，仿真原理如图4所示。

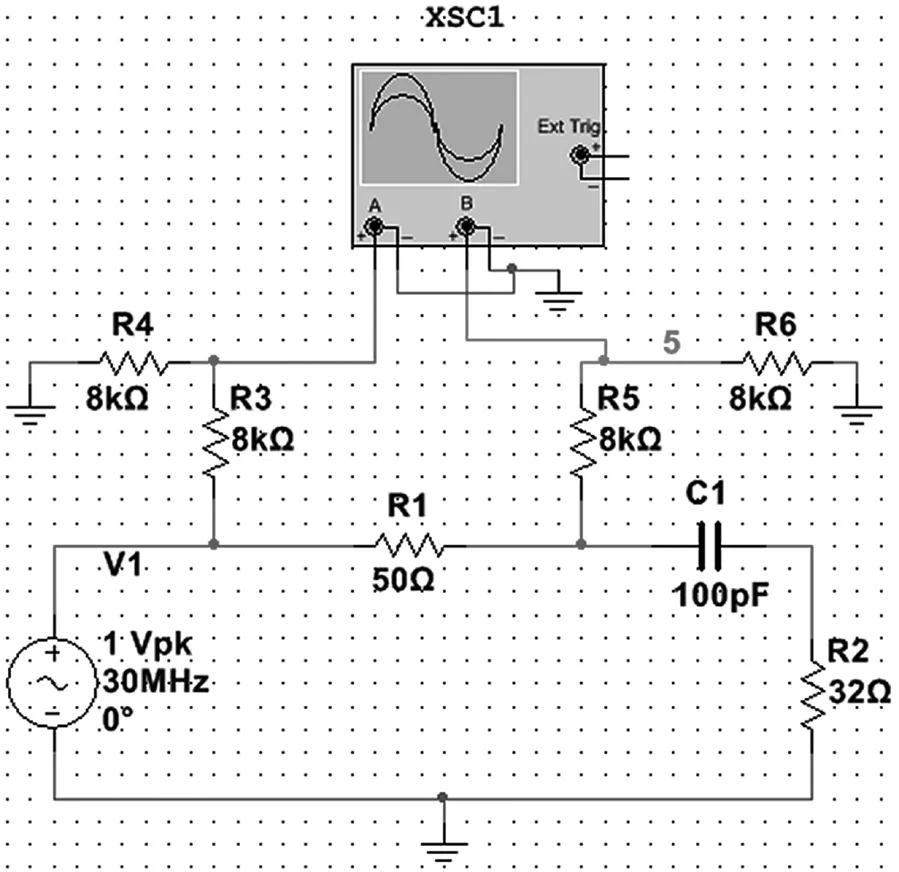
图4 矢量阻抗检测电路Multisim仿真原理

输出仿真数据，借助Matlab软件计算负载阻抗。时域输出波形如图5所示。

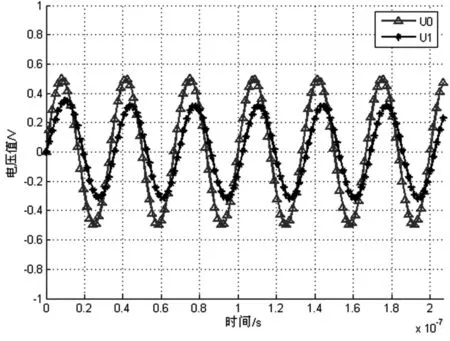
图5 矢量阻抗检测时域波形（Z0=50Ω）

根据③式计算得到的负载阻抗Z=31.17-j52.65，与理想值32-j53.05吻合接近。当负载阻抗变化（纯感、纯容、感性负载、容性负载）时，采用上述相同方法，对比不同频率点下桥式检测阻抗与理论阻抗，如表1所示。

从以上仿真数据可以看出，在全频段内，桥式检测阻抗与理论阻抗误差百分比不超过2%，检测精度优于传统检测方法（5%～10%）。

3.2 检测误差分析

在工程实现中，采样数据与真实数据会存在偏差，有必要对采样数据的偏差对计算引入的误差进行分析，以评估该误差是否在可接受范围内。

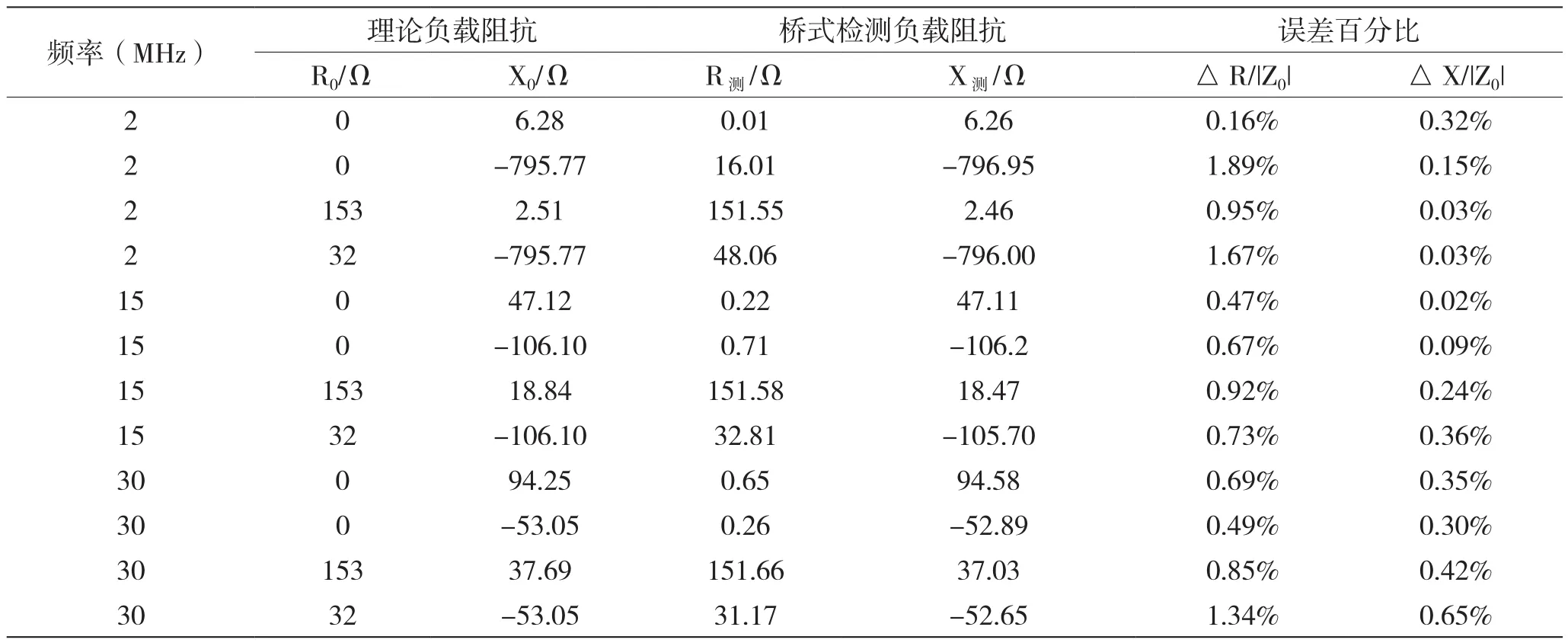
表1 理论负载阻抗与桥式检测阻抗仿真对比（样点数量512，采样速率65 MHz）

对固定的相位差φ0=-π/9，U0=1，U1=0.2，每个采样点存在幅度为5%的随机偏差，总样点数为512，采样速率为65 MHz，在2～30 MHz内以扫频方式（步进为100 kHz），误差分析结果如图6所示。

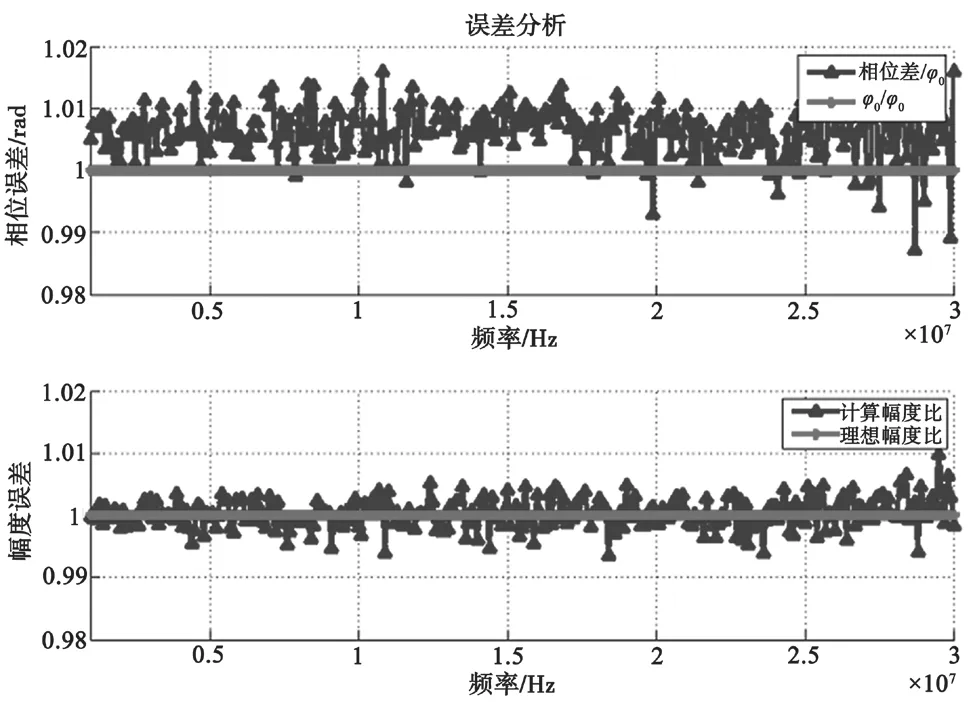
图6 样点偏差幅度为5%误差分析

当每个样点的随机偏差幅度为10%时，误差分析如图7所示。

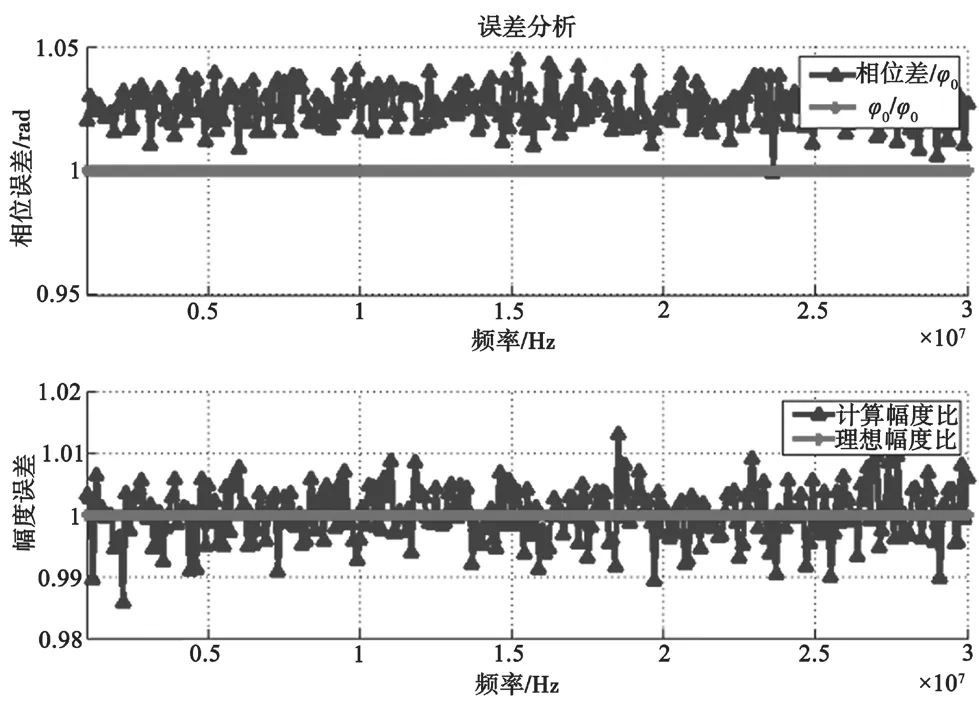
图7 样点偏差幅度为10%误差分析

从以上误差分析可以看出，当样点偏差在5%时，计算的相位误差小于2%，幅度误差小于1%；当样点偏差在10%时，计算的相位误差小于5%，幅度误差小于2%。

4 结 语

矢量阻抗检测模块作为天线调谐器的关键模块，是天调执行调谐算法的基础，其检测精度直接决定了天调的调谐精度。本文分析了传统短波矢量阻抗检测器的检测原理及存在问题，提出一种新型桥式检测器的设计方法，该检测方法具有电路复杂度低、低功耗、小体积等特点，处理算法简洁、高效。通过Multisim与Matlab进行联合仿真，验证了新型阻抗检测器的可行性，并对采样数据存在随机偏差时引入的检测误差进行定量分析。