基于PGC技术的水下极低频信号检测解调方式研究*
2019-12-11何如龙孙剑平隗小斐
何如龙,孙剑平,隗小斐
(1.海军工程大学 电子工程学院,湖北 武汉 430033;2.海参指挥保障大队,北京 100086)
0 引 言
极低频信号(这里指的是0~20 Hz)也叫作次声波,普遍存在于人类各项活动与自然领域。火山喷发、海啸、地震还有轮船航行与核爆炸等,均会产生大量的极低频信号。因为这一信号在水下具有诸多特点,如衰减速度慢、损耗较低、传播距离相对较远等,所以它的应用得到了更多领域的重视。为了全面适应水声学应用尤其是水下反潜战的各种需求,在传感技术持续进步、发展的基础上产生了光纤水听器[1]。运用传感器进行全面的探测,在地震事先预测、次声监测、水下反潜战及低频声纳等诸多军用、民用领域均有着极其宽广的应用空间。换句话说,极低频信号检测是日后光纤传感技术发展及应用的主要趋向。
2007年,Beverini N等[2]人利用光纤做传感单元,采用非平衡Mach-Zehnder实现了全面的解调[3],同时极低频传感系统的探测频率也实现了由0.05 Hz增加至几十赫兹。2010年,学者叶欣[4]等人以干涉仪与相位生成载波(Phase Generation Carrier,PGC)解调技术为基础,将低频信号传感系统的最低探测频率降至1 Hz。
干涉型光纤传感器存在多种信号检验方法,当中PGC解调方法[5]因为构造单一、动态范畴较大和灵活度较高等优点,拥有普遍的运用区域及较大的实力而受到大家的关注。为实现对水声信号的检测,国内外提出多种PGC解调方法,主要包含有相位抽取法、微分交叉相乘(Differential Cross Multiplication,DCM)、相位抽取法以及反正切(Arctangent)等[6]。随着研究的深入,当PGC技术运用在极低频信号解调时,由于噪声和温漂等外部的干预,信号难以经过滤波分开,因此PGC算法中无法用高通滤波区分信号。所以,有关DCM式PGC计算法在积分中形成直流滤波项不能清除,进而会从中加入直流漂移项[7],而Arctangent式PGC的计算法没有直流项问题,所以对极低频信号的精准解调有望完成。
1 PGC解调原理
当极低频待测信号应用于光纤干涉仪中的信号臂时,干涉仪两臂之间的相位差将随着待检测信号的改变而发生一定的变化。假设φs是这一信号所引起的干涉仪两臂之间的相位差[8],那么光纤干涉仪所输出的各类干涉信号可以表示为:

A=I0表示干涉仪入射光强,B=I0k,k表示干涉条纹可见度。
在PGC解调技术中,经过在干涉仪的一端实行相位调动,光纤干涉仪所输出的PGC干涉信号可表示为[9]:

ω0表示PGC调制载波的角频率,C表示相位调制深度。当DCM和Arctangent两种算法运用在极低频信号解调时,在没有检测的信号之外,外面环境的噪声和温度漂移等物理量处在同一频段,很难经过滤波器滤除去其干预,使得用在极低频信号解调的PGC算法无法包括高通滤波过程。可见,DCM式PGC算法和Arctangent式PGC算法应该用在极低频信号解调时,流程算法如图1所示[10]。
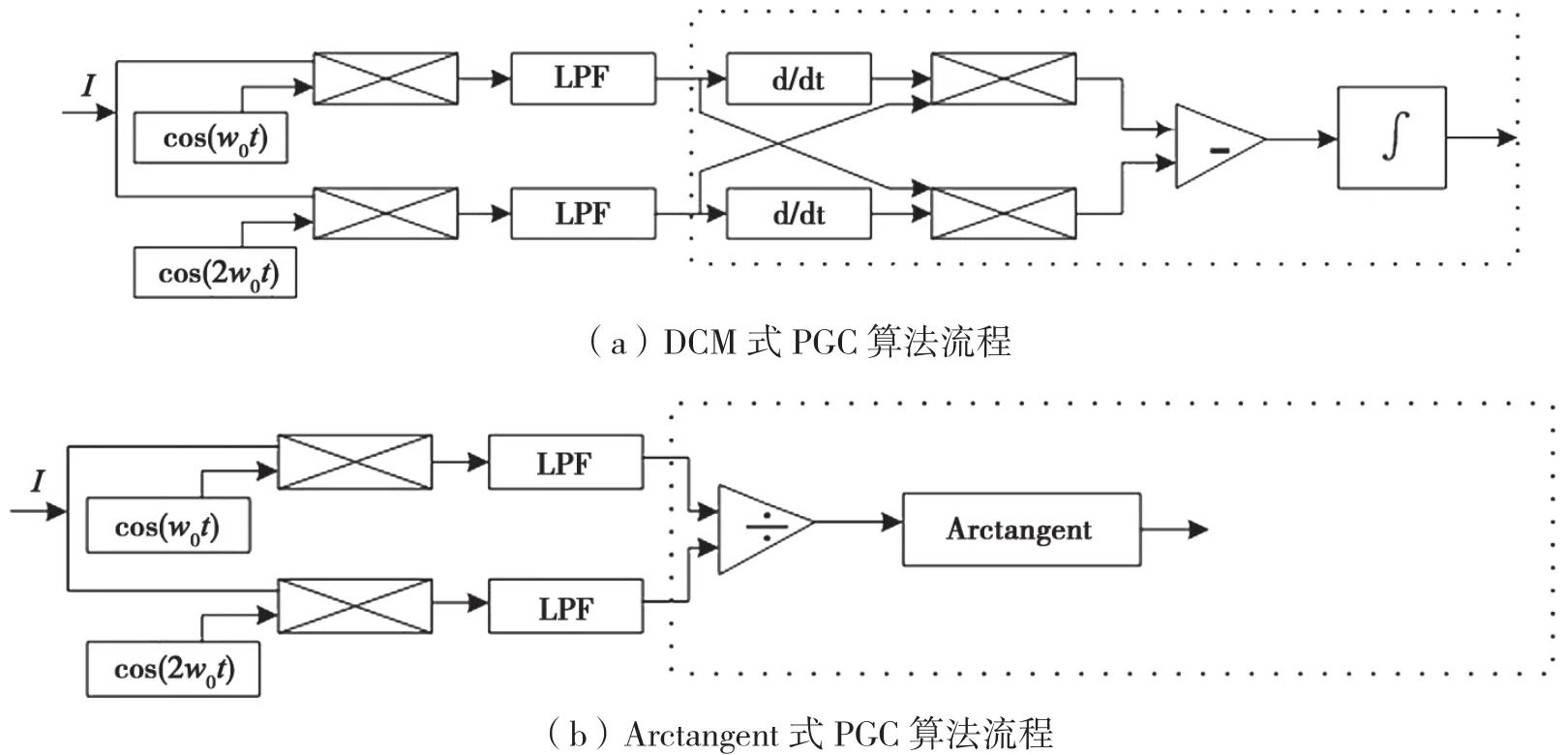
图1 极低频PGC解调算法原理
1.1 DCM式PGC算法
分析极低频信号解调PGC算法时,假设待检测信号为单频余弦信号[11],通常可表示为:

式中AS表示信号振幅,φs表示信号初始相位。针对DCM式的PGC算法,把式(3)代入式(2),分别与载波函数cos(ω0t)及其倍频函数cos(2ω0t)互相混频后进行低通滤波。考虑到低通滤波器对各类输入信号的相位产生了一定的延迟φf,后两段信号可以表示为:
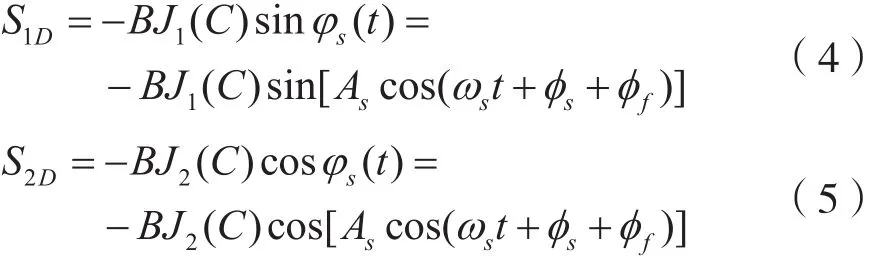
式中,J1(C)与J2(C)分别代表第一类1阶和2阶贝塞尔函数。对式(4)和式(5)进行全面微分交叉相乘:

针对式(6)积分,得出:
当中的第一项是恢复的待检测信号,对应传送信号有φf的相位缓慢;第二项是和待检测信号初始相位及滤波器相位缓慢有关的直流项。因为计算法中的积分后不再包括高通滤波过程,直流项将不能进行清除,所以在过程中加进了直流漂移。PGC算法中经常采取拥有线性相位的一定长冲激响应(Finite Impulse Response,FIR)滤波器,以确保低通滤波无法对输送信号形成相位失真。有关频率为fs的待检测信号,根据FIR低通滤波器引进的相位延迟为:

式中f代表系统采样频率,N代表低通滤波器的主要阶数。由式(8)能够得出,在系统采样频率不发生变化的情况下,φf取决于滤波器主要阶数及待测信号频率。实际应用中,待检测信号经常包括有不相同的频率分量和不一样的相位延迟,经过积分运算后每个分量将具有不一样大小的直流项,最后不能精准恢复待检测信号。所以运用DCM式PGC解调的算法不能完成对极低频信号进行精准解调[12]。
1.2 Arctangent式PGC算法
针对Arctangent式PGC算法,待测信号通过低通滤波及混沌后可表示为:
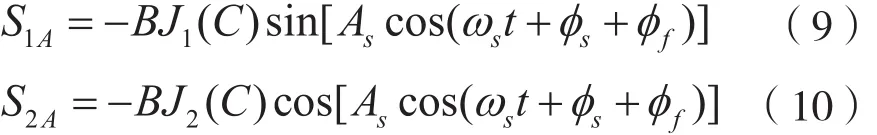
将式(9)和式(10)直接相除,得到:
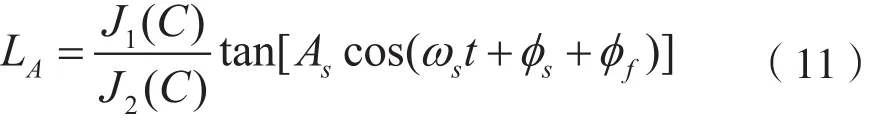
根据式(11)求出反正切,将C=2.63 rad作为主要相位调制深度,使J1(C)=J2(C),可得:

比较式(3)与式(12)能够得出,因为Arctangent式的PGC算法中不存在任何积分项,它的解调结果和原信号相比仅有相位延迟而不存在直流漂移,所以运用这一技术可完成对极低频信号的精准调制解调。
2 PGC解调算法对比仿真
运用Matlab仿真工具对Arctangent式与DCM式两种PGC调制解调算法极低频信号展开全面的仿真。在不同的参数下对其进行仿真,对比了这两种算法对同一个极低频信号所做出的仿真分析结果。因为待检测信号处在低于20 Hz的极低频段,所以在仿真过程中将PGC调制载波频率设置成100 Hz,将C=2.63 rad作为主要相位调制深度,将采样速率定格为1 ks/s,将100 ks当作数据处理帧长[13]。
仿真时,假设待检测的是极低频信号中的余弦信号 φs(t)=Ascos(2πfst+φs),取 As=0.1、fs=0.05 Hz,分别利用DCM式和Arctangent式PGC解调算法对极低频信号做调制解调。在确保滤波各项性能均完善的前提条件下,选择阶数相对较低的滤波器(即N=501)。分别选择待检测信号初始相位值φs=0、π/3、π/6,仿真结果如图2所示。
将不同参数代入式(7)与式(12),经过运算能够得出DCM式与Arctangent式两种PGC算法解调结果中直流漂移的理论,它的值与仿真结果的对比如表1所示,可见模拟仿真结果和理论分析基本一致。

图2 不同解调算法性能对比仿真结果

表1 信号初始相位引起的直流项漂移理论与仿真结果
3 结 语
提出并完成了一项用基于光纤干涉原理的用于极低频信号监测的PGC调制解调技术。理论上解析了DCM式及Arctangent式两种PGC计算法,运用matlab软件完成了模拟仿真,且针对两种仿真结果进行对比研究。理论及测验结果显示,Arctangent式PGC算法没有DCM式算法存在的直流漂移弊端,可以更好地完成对极低频信号的精准解调。基于这一算法搭建的极低频光纤水听系统有望在水下低频声纳、海啸预警、地震事先预测以及次声监测等诸多领域发挥关键作用。
