支持隐私保护的k 近邻分类器∗
2019-12-11王安迪周福才
徐 剑 , 王安迪 , 毕 猛,3 , 周福才
1(东北大学 软件学院,辽宁 沈阳 110169)
2(信息安全国家重点实验室(中国科学院 信息工程研究所),北京 100093)
3(沈阳工业大学,辽宁 沈阳 110023)
分类器是数据挖掘中对样本进行分类的方法的统称.其设计目标是在通过学习后,能够将数据分到已知类别.分类器不仅应用在搜索引擎以及各种检索程序中,而且也大量应用在数据分析与预测领域.kNN 分类器是一种重要的分类器,广泛应用于生物信息学、股票预测、网页分类、鸢尾花类别预测等领域.
分类器在广泛应用的同时,也产生了严重的用户隐私泄露问题[1,2],一旦泄露,会给数据拥有者带来危害.比如,不法分子盗取患者癌症信息,利用患者迫切希望治愈的心理,向患者销售高价药品,骗取钱财;在利用kNN 进行股票预测时,如果股民的个股信息在分类过程中被泄露,就会给股票市场带来混乱.分类器处理的数据量大、种类多,与之相关的用户数据隐私保护形势也非常严峻.目前,针对数据分类过程中的隐私保护研究主要集中在密文数据运算方面,但是该类技术也存在如下问题:(1)一些分类器对密文数据的运算复杂,运算效率较低;(2)加密技术针对的是特定的分类器,缺乏普适性.
kNN 分类器是监督学习中“懒惰学习”(lazy learning)的典型代表,监督学习过程由两个阶段构成.
(1)样本训练阶段:在此阶段,首先获取在准备工作阶段处理好的训练数据;然后根据分类器类型选择分类算法,对训练数据进行训练得到模型W,以此作为分类阶段的一项输入.
(2)应用阶段(分类阶段):分类器C通过模型W对测试向量X进行分类预测,得到最终的分类结果C(W,X).
在样本训练和分类阶段,都可能发生用户隐私信息的泄露:在样本训练阶段,数据拥有者不希望自己拥有的数据信息被泄露出去,甚至对训练者也要进行保密,这就需要对训练数据进行加密处理;在分类阶段,训练者会将得到的模型W作为分类器的构成部分,并将分类器发布出去提供服务,但不希望成果被第三方获取,这就需要对分类模型和测试向量进行加密.总而言之,分类器要保证数据的隐私性必须从两方面入手:(1)训练数据集和模型W的隐私保护;(2)测试向量X和分类结果C(W,X)的隐私保护.
目前已有一些关于分类器隐私保护的研究成果,但大多数方案都是针对训练阶段数据的隐私保护,很少有针对分类模型和分类过程的保护.因此,设计基于加密数据的基本操作加密协议并以模块化顺序组合的方法构造安全的分类器,使其从训练阶段到分类过程都能保证安全性,同时保证待测数据能够获得一个准确的类别,是当前机器学习隐私保护的重要研究方向之一.
1 相关工作
分类器的构造和实施过程就决定其在隐私保护方面存在隐患,例如,在训练样本上执行分类器算法,生成分类模型,很容易造成样本数据的泄露;在测试样本上执行分类模型,生成预测结果时,客户端会很容易得到分类模型,而服务器端也可以轻易获取到输入的测试数据.因此,分类器在样本训练和分类阶段的数据隐私问题已成为分类器隐私保护中最为重要的研究内容之一.
(1)样本训练阶段
为了保证在样本训练阶段原始数据的隐私性,应将原始数据隐藏起来,在此阶段,不同的分类器会选择不同的算法来训练原始数据,比如贝叶斯算法、支持向量算法、决策树算法等.这些算法包含了点积运算、加法运算、比较运算.为了保证隐藏后的数据仍然能够进行上述运算,本阶段使用的隐私保护技术应满足3 个方面的要求:(1)不改变原始数据的整体分布趋势;(2)不能从隐藏后的数据中直接推算出原始数据值;(3)确保经过变换后的数据不会降低分类器的分类效果.目前,研究人员采用的技术主要分两类:数据干扰和数据加密.文献[3]提出一种基于非线性维数降低(即非度量多维缩放)来干扰原始数据的隐私保护框架,使用k-Nearest Neighbor分类算法对分类任务中的新型隐私保护数据挖掘(privacy-preserving data mining,简称PPDM)方法进行了测试,在隐藏隐私数据的同时,保证了数据的有效性;文献[4]提出了数据扰动技术并利用该技术构建了决策树分类器,之后,相继提出了不同的扰动方法[5,6].但是,扰动技术不能保证密文数据的语义安全,且数据添加了统计噪声易造成分类器的分类精度下降.文献[7]提出了两方参与的决策树分类器,其假定数据分布在两方;文献[8-10]利用安全多方计算(secure multi-party computation,简称SMC)技术构造了安全的分类器;文献[11]设计了一种基于主成分分析(primary component analysis,简称PCA)的协同学习隐私保护方法,其利用PCA 实现了在协同学习过程中对压缩数据的隐私保护;文献[12]设计了一种加法同态代理聚合方案实现了云端患者的历史数据的隐私保护,引入了隐私保护的top-k疾病名称检索协议保证了朴素贝叶斯分类器的安全性;文献[13]提出了一种分布式系统的隐私保护数据分类和相似性评估方案,该方案在分类和相似度评估过程中不泄露任何关于新到达数据和训练模型的信息,其最终的分类结果除外;文献[14]提出了将线性分类器和IPE(inner product encryption)相结合的方法来对加密数据进行分类,其隐私保护分类方案允许用户的数据被加密,但服务器能够获知最终的加密结果;文献[15]设计了实用的安全模型,通过研究在安全的两方计算框架中的一些多元统计分析方法,生成了一些构造块,解决了安全的两方多元线性回归问题和安全的两方多变量问题;文献[16]基于安全多方协议与同态加密方案训练几种简单的分类器,例如线性分类器,该分类器是支持加密数据分类的,但是其构造的模型安全性较低,导致客户端不仅能够得知最终的分类结果,而且可能会获取分类模型的信息,造成分类模型信息的泄露.综上所述,在样本训练阶段不仅要隐藏原始数据,还要将分类规则进行隐藏,即保护服务器参与分类数据的隐私性,防止通过模型或分类过程推导出个人信息.
(2)分类阶段
在分类阶段,支持用户数据隐私性保护的研究成果较少.在文献[17]中,第三方运行医疗预测函数对全同态加密(fully homomorphic encryption,简称FHE)的患者数据进行运算,得到预测结果.该算法仅隐藏了来自云端的输入数据,在分类阶段,任何一方都可以获取到分类模型,容易泄露患者隐私给第三方或各参与方.文献[18,19]构造了线性分支程序的安全评估,用此实现了心电图(electrocardiogram,简称ECG)信号的安全分类.这项技术是基于finely-tuned garbled 电路的,虽然保证了分类过程的安全性,但分支程序的运行速度较慢.文献[20]利用神经网络[21]构造了安全的分类器,这是感知器分类器的泛化,使神经网络分类器能够支持对密文数据的分类.
综上所述,在分类样本训练阶段的隐私保护研究成果较多,在分类过程中的隐私保护研究成果则不多见,容易造成用户隐私信息的泄露.为此,本文首先对kNN 分类器的操作进行分析,提取出从样本训练阶段到分类过程中所包含的基本操作,包括加法、乘法、点积、比较;针对上述基本操作,设计了相应的安全协议,然后以模块化顺序组合的方式将其组合生成PP-kNN 分类器,从而保证了样本训练阶段和分类过程的数据隐私性.本文所设计的PP-kNN 分类器的基本操作的隐私保护协议是基于差分隐私的,给加密数据加入噪声,防止在交互式环境中信息的泄露.在设计基本操作的安全协议时,选择了两种同态加密方案对数据进行加密,以增加隐私保护的强度.同时,所设计的基本协议在半诚实模型下是安全的,模块化顺序组合方法在该模型下也是安全的,因此通过顺序组合构造的PP-kNN 分类器也是安全的.
本文第1 节对kNN 分类器和本文使用的加密方法进行描述.第2 节给出基本操作安全协议的设计.第3 节详细说明支持隐私保护的kNN 分类器的构造过程.第4 节从计算代价、存储代价等方面对基本操作安全协议及PP-kNN 分类器进行性能评估.最后,对全文进行总结.
2 预备知识
2.1 kNN分类器
在kNN 分类过程中,待分类对象的类别可以通过在它附近的训练数据的类别来确定,所以采取的策略就是找到离待分类对象最近的k个邻居进行分析.kNN 分类器的工作流程如下.
Step 1.确定k值(最近邻居的个数).一般为奇数,通常是采用交叉检验来确定(经验规则:k一般低于训练样本数的平方根).
Step 2.确定距离度量公式.以文本分类为例,采用夹角余弦,得出待分类数据点和所有已知分类数据点的夹角余弦值.按夹角余弦值从大到小排列,获取距离最近的k个样本(夹角余弦值越大,角度就越小,距离也就越近).
•距离度量公式还可使用欧式距离:

Step 3.统计这k个样本点中各个类别的数量classCount[i].通过比较,得到类别数量最多的样本对应的分类ci,该类便是待分类样本所属分类.
2.2 加密方法
2.2.1 加密方案
本文使用了两种同态加密方案(goldwasser-micali 的二次剩余加密系统(QR)[22]和Paillier 加密系统[23])及一种全同态加密方案(FHE)[24]对数据进行加密,前两种加密方案满足加法同态,后一种方案同时满足加法同态与乘法同态.同态加密体制[25]的加法同态与乘法同态的概要描述如下.
设R和S为整数环,R表示明文空间,S表示密文空间.a,b∈R,E是R→S上的加密函数.如果存在算法PLUS和MULT,使其满足:

这样可以利用E(a)和E(b)的值计算出E(a+b)和E(a×b),而不需要知道a,b的值.它分别满足加法同态和乘法同态.
2.2.2 加密假设
下面对本文用到的二次剩余假设、判定性合数剩余假设和判定性RLWE 困难性假设进行介绍.
1)二次剩余假设.假设N=p×q(p,q为奇素数),ℚℝN为模N的二次剩余集,ℚℕℝN为模N二次非剩余集(如果x是模N的非平方剩余,则x∈ℚℕℝN,且Jacobi符号等于1).{(N,ℚℝN):|N|=λ}和{(N,ℚℕℝN):|N|=λ}是概率多项式时间计算不可区分的.
2)判定性合数剩余假设.令N=p×q,|N|=λ,N为两个值不等但长度相等的奇素数p和q乘积.z称为模N2的第N个剩余,如果存在,使得z=yNmodN2,其中,第N个剩余和第N个非剩余是概率多项式时间计算不可区分的.
3)判定性RLWE 困难性假设.对于安全参数λ,令f(x)=xd+1,其中,d是2 的方幂,令q≥2 为一个整数.令整数多项式环R=ℤ[x]/f(x),Rq=R/qR,χ是R上的分布.DRLWEd,q,χ问题是指对下面2 种分布进行区分:(1)(ai,bi)随机均匀取自;(2)首先随机均匀选取s←Rq,然后随机均匀选取ai←Rq和ei←χ并计算bi=ai⋅s+ei,最终得到DRLWEd,q,χ假设是指DRLWEd,q,χ问题中的两种分布是不可区分的.
一般来讲,噪声分布χ通常为高斯分布.
2.2.3 安全两方计算框架与模块化顺序组合
本文的基本操作安全协议都是两方协议,其安全性依赖于两方的安全计算框架.而本文将基本操作安全协议通过模块顺序组合技术构成安全的分类器,因此分类器的安全性应遵循模块化顺序组合的安全性和安全两方计算框架的安全性.定义1 和定理1 分别对半诚实模型下的安全两方计算定义和模块化顺序组合定理进行了描述.
定义1(半诚实模型下的安全性).设f=(fA,fB)为概率多项式函数,A,B为参与方,fA(相应地,fB)记为f(a,b)的第一元素(相应地,第2 个元素),Π为计算f的两方协议.A输入a,B输入b,A,B在通过Π和安全参数λ执行f(a,b)过程中的视图标记为VA(λ,a,b),即,其中,rA为A内部掷币过程的输出,为参与方A接收到的第i个消息,B的视图标记与A类同.
在协议Π执行完毕后,A,B基于输入(a,b)的输出分别记为,显然,输出包含在参与者的视图中,且有:
(一般情况)称Π秘密地计算了f,若存在概率多项式算法分别标记为SA和SB,且使得等式(1)和等式(2)成立.
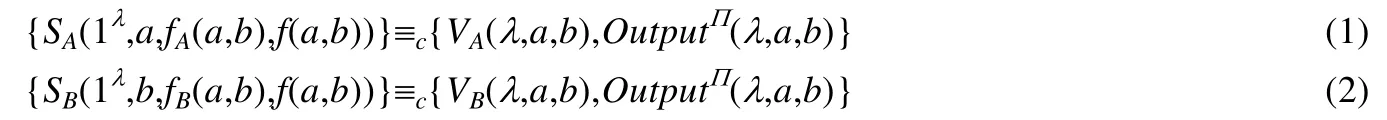
其中,≡c表示概率多项式时间计算不可区分,忽略不计安全参数λ.这里需要强调的是,VA(λ,a,b),VB(λ,a,b),为相关的随机变量,由相同的随机执行函数定义.特别地,完全由Vi(λ,a,b)确定.
(确定情况)对一个确定的函数f,称Π秘密地计算了f,如果存在概率多项式算法分别标记为SA和SB,且使得等式(3)和等式(4)成立.

为了简化符号和证明,本文在确定情况下的符号表示省略了安全参数.由于主要考虑确定性函数f,因此在进行安全性证明时,统一使用等式(3)和等式(4)的符号表示.
模块化顺序组合方法借鉴了文献[26]中安全协议模块化组合技术,通过顺序组合的方式,一个接一个简单地运行多个安全协议,构成了完整的、安全的分类器协议.其思想是:首先,为给定任务设计一个“高级”协议,假设可以安全的执行其他简单的子任务;然后,为简单的子任务设计安全协议;最后,通过在“高级”协议中插入简单的安全协议作为子例程,为给定任务构建一个完整的协议.
定理1(模块化顺序组合).设f1,…,fm和g为两方概率多项式函数,假设协议ρ1,…,ρm基于半诚实模型分别安全地评估函数f1,…,fm,协议Π基于半诚实模型安全地评估函数g,同时使用子程序调用理想函数f1,…,fm.然后从协议Π导出的协议通过替换协议Π的每个子程序调用安全地评估g,则称在半诚实模型上安全评估了函数g.
3 面向基本操作的安全协议
3.1 符号描述
在进行面向基本操作的安全协议构造之前,先给出相关符号的描述.安全协议由两方构成,协议双方分别记作A和B.分类器的双方分别记作C和S,C表示客户端,S表示服务器.
本文的加密方案有3 种:QR 表示二次剩余加密方案,Paillier 表示Paillier 加密方案,FHE 表示全同态加密方案.在实现第3.2.1 节的比较协议时,使用了Damgard,Geisler and Krøigaard(DGK)加密方案[27],符号描述见表1.

Table 1 Notation description表1 符号描述
对于常量b,a←b表示将b赋值给a.
对于分布D,a←D表示在分布D中随机抽样一个元素a.
3.2 比较协议
比较协议是构造分类器的安全协议之一,用于比较两个用Paillier 加密的密文数据,获取QR 加密的比较结果,比较协议的相关符号描述见表2.

Table 2 Comparison protocol表2 比较协议
3.2.1 改进的DGK 比较协议
DGK 比较协议[28]是两方协议,参与方分别记为A,B,输入分别为整数a,b,其比特位数相同,输出分别为δA,δB.其计算思路是,从最高有效位开始依次比较ai,bi的值,记录比较结果,其中,0≤i≤l,l表示比特位数,s=a-2⋅δB,δB={0,1}由B方随机选取.若ci=0,则δA=1;否则,δA=0,δA⊕δB=(a≤b).值得注意的是,在此过程中,ai,bi都是以DGK 加密的密文形式参与运算.
表2 的第1 行是基于DGK 比较协议的,并对其进行修改以适应PP-kNN 分类器的应用需求.其目的是比较两个未加密的数据a和b,得出通过QR 加密的比较结果.本文增加以下操作满足应用需求:(1)A通过QR 对δA进行加密,将加密的[δA]发送给B;(2)B通过 QR 对δB进行加密,计算[δA]⋅[δB].因为[δA]⋅[δB]≡[δA⊕δB]modN≡ [a≤b],因此通过计算[δA]⋅[δB],可得出比较结果[a≤b].在此过程中,B没有QR 私钥,因此无法对δA进行解密,保证了计算过程中数据的安全性.
3.2.2 加密数据的比较协议
本文的比较协议是两方协议,其中,一方A拥有待比较数据〚a〛,〚b〛,另一方B拥有解密密钥.本文的比较协议是基于Veugen 比较协议[29]的,并对其进行了修改以适应PP-kNN 分类器的应用需求.具体修改如下:首先,在Veugen 的比较协议中调用一个子程序实现两个未加密数据的比较,本文使用表2 第1 行的比较协议替换该子程序;然后,将该子程序的两方角色进行置换,即输出方由A方置换为B方;然后,B进行计算并将计算结果发送给A,A进行解密得到未加密的比较结果.协议1 是对加密数据比较协议的描述.
比较协议的主要思想是,计算x=2l+b-a,得到x的第l+1 位(这一位正好对应2l)的值:若是1,则a≤b;否则,a>b.本文的假设加密方案是加法同态的,其中,N表示Paillier 加密的模量.
协议1.加密数据的比较协议.
输入方A:〚a〛,〚b〛,a和b的比特长度l,私钥SKQR,公钥PKP.
输入方B:私钥SKP,公钥PKQR,比特长度l;
输出方A:(a≤b).
1:A计算加密数据〚a〛,〚b〛,即〚x〛←〚b〛⋅〚2l〛⋅〚a〛-1modN2▷x←b+2l-a
2:A从数据域(0,2λ+l)∩ℤ中随机选择数r,即r←(0,2λ+l)∩ℤ
3:A为〚x〛增加噪音〚r〛,即〚z〛←〚x〛⋅〚r〛 modN2▷z←x+r
4:A将〚z〛发送给B
5:B解密〚z〛
6:A:c←rmod 2l
7:B:d←zmod 2l
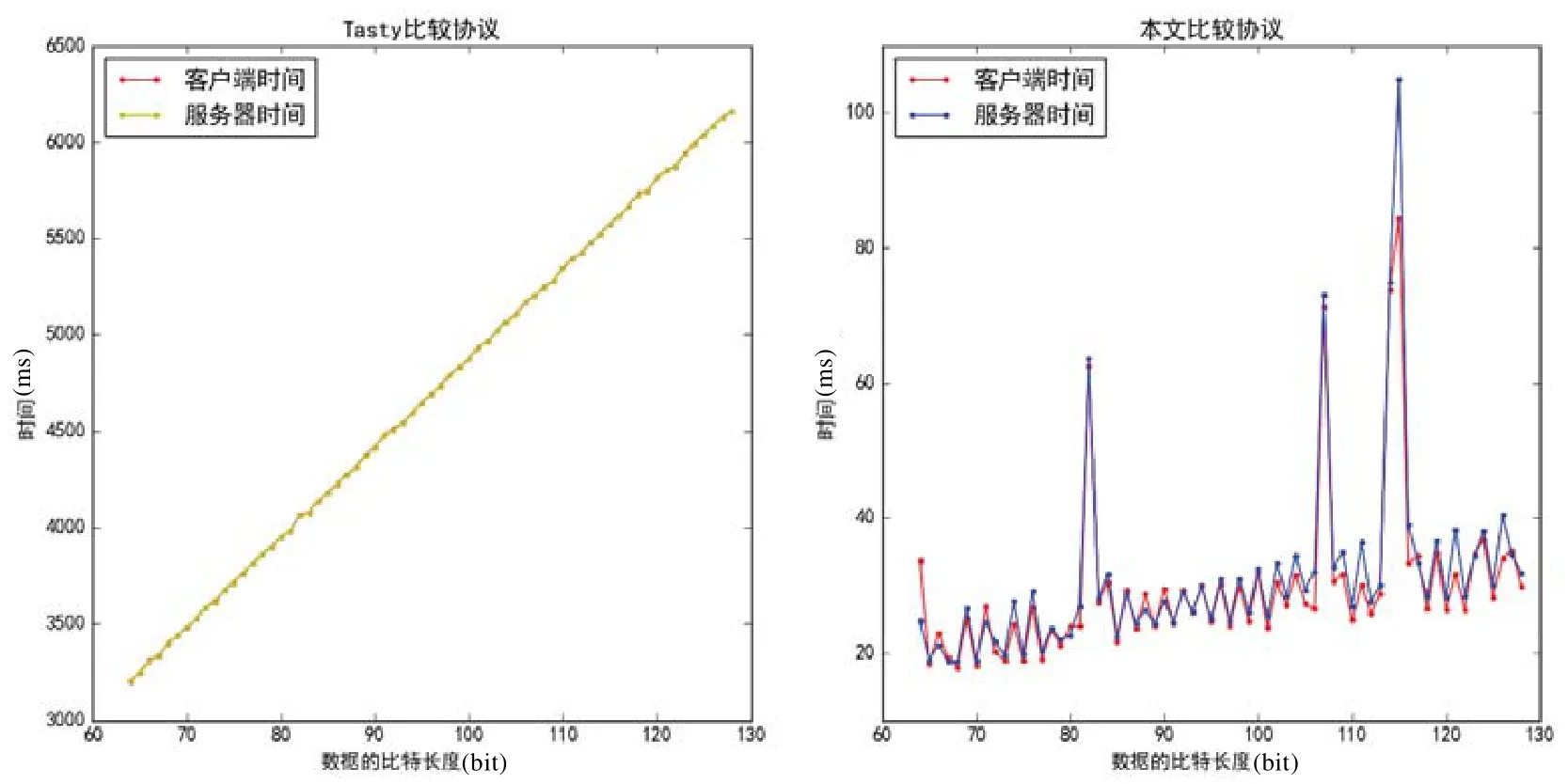
8:调用第3.2.1 节修改的DGK 比较协议,A,B作为输入方,输入数据分别为c,d,B,得到比较结果[t′],其中,t′=(d 9:A对r的第l+1 位rl+1进行加密,将加密的[rl+1]值传送给B 10:B对z的第l+1 位zl+1进行加密,得到[zl+1] 11:B计算第l+1 位的值并赋给[t],即[t]←[t′]⋅[zl+1]⋅[rl+1]▷t←t′⊕zl+1⊕rl+1 12:B将[t]发送给A 13:A解密[t]得到t 3.2.3 比较协议的正确性分析 协议1 中,a,b是l位整数,x=2l+b-a是l+1 位整数,x÷2l表示x的最高有效位,其运算为t=t′⊕zl+1⊕rl+1,当该值等于1 时,a≤b.下面将给出其正确性证明. 证明:x是l+1 位整数,x÷2l表示x的最高有效位,即第l+1 位的值,此时有: 其中,0≤xmod 2l≤2l. 因为z=x+r,所以有: 当(xmod 2l)+(rmod 2l)<2l时,有: 当(xmod 2l)+(rmod 2l)≥2l时,有: 将公式(5)、公式(6)整合可得: 则t′=0⇔(xmod 2l)+(rmod 2l)<2l,即 •当t′=0 时,zmod 2l=(xmod 2l)+(rmod 2l); •当t′≠0 时,zmod 2l=(xmod 2l)+(rmod 2l)-2l. 因此,t′=0⇔zmod 2l=(xmod 2l)+(rmod 2l)⇔zmod 2l≥rmod 2l⇔d≥c. 因为x÷2l的值非0 即1,所以有x÷2l=(z÷2l)-(r÷2l)-t′ mod 2=zl+1⊕rl+1⊕t′.□ 综上所述,x的最高有效位可以通过zl+1⊕rl+1⊕t′正确计算,因此本文的比较协议是正确的. 3.2.4 比较协议在半诚实模型下的安全性分析 假设加密位[t′]是通过理想计算得到的.本节分析比较协议在半诚实模型下的安全性,并使用模块化顺序组合定理(定理1)得出结论. A方的元组表示为VA=(〚a〛,〚b〛,l,SKQR,PKP;r,coins,[t]),其中,coins为加密2l,r,rl+1的随机数,给定(〚a〛,〚b〛,l,SKQR,PKP,a≤b),模拟器SA的构建过程如下. 元组VA(〚a〛,〚b〛,l,SKQR,PKQR,SKP,PKP)和SA(〚a〛,〚b〛,SKQR,PKP,a≤b)的分布是相同的,因为这两种情景下的随机值取值相同且QR 加密的是同一比特位. B方元组表示为其中,coins为加密zl+1的随机数,则模拟器SB(PKQR,SKP,l)的构造过程如下. 随机变量coins和生成方式相同且与其他参数独立,因此, 从第3.2.2 节加密数据比较协议可知,z=x+rmodN,其中,x为l位整数,r为λ+l位整数. 因为QR 是语义安全的,因此有: 本文使用模块化顺序组合来实现协议执行过程中的安全性衔接,使用改进的DGK 协议取代了理想计算得到的[t′],使用定理1 证明了其在半诚实模型下的安全性.综上所述,本文的比较协议在半诚实模型下是安全的. 本文通过欧式距离计算测试样本与训练样本之间的距离.为了保证PP-kNN 分类器中距离计算的安全性,本文设计了点积协议. 协议处理的是密文数据,所有操作皆在密文空间进行.它由A和B两方参与:A表示客户端,输入测试样本,记作x;B表示服务器,输入训练样本,记作y.协议2 是点积协议的具体描述. 协议2.点积协议. 输入方A:x=(x1,…,xd)∈ℤd,公钥PKFHE. 输入方B:y=(y1,…,yd)∈ℤd,私钥SKFHE. 输出方A:〚[v]〛. 1:B对向量y1,…,yd进行加密,然后将加密后的数据〚[y]〛发送给A 2:A对向量x1,…,xd进行加密,得到加密数据〚[x]〛 3:A计算〚z〛←〚y〛⋅〚x〛-1modN2▷z=y-x 4:A计算,然后输出加密的 协议2 在半诚实模型下的安全性:在本协议中,B未接收任何信息,仅提供了数据及用于加密的随机数,则模拟器SB可表示为SB(y,SKFHE)=(y,SKFHE;coins)=VB(x,y,SKFHE,PKFHE),其中,coins为B方生成的随机数.A的元组表示为VA(x,PKFHE;rA;〚z1〛,…,〚zn〛),模拟器SA的构造过程如下. Step 1.生成n个FHE 加密的0:cn,…,c0. coins和的分布相同,因此, 由于FHE 加密方案的语义安全,所以有: 函数f满足f(x,y,SKFHE,PKFHE)=(〚[〈z,z〉]〛,∅)时,有: 本协议中,B将加密好的数据〚[y]〛发送给A,A没有私钥无法对其解密,保证了数据的安全性.加密方案是加法与乘法同态的,因此密文数据计算过程是安全且同态的.上述过程通过定义1 证明了其在半诚实模型下的安全性.综上所述,本文的点积协议在半诚实模型下是安全的. PP-kNN 分类器由点积协议、比较协议通过顺序组合的方式构造而成,点积协议的输入与输出数据是FHE进行加密的密文数据,比较协议的输入数据是Paillier 进行加密的密文数据.为了保证PP-kNN 分类器的点积协议和比较协议可以进行模块化顺序组合,本文设计了加密方案转换协议,实现了从一种加密方案到另一种加密方案的转换.协议3 是加密方案转换协议的描述. 协议3.加密方案转换协议. 输入方A:〚c〛1,公钥PK1,PK2. 输入方B:密钥SK1,SK2. 输出方A:〚c〛2. 1:A均匀随机选择一个数r←M 2:A计算〚c′〛1←〚c〛1⋅〚r〛1将〚c′〛1发送给B▷Blindc 3:B解密后得到c′,用E2重新加密 4:B将重新加密后的〚c′〛2发送给A 5:A去除噪音〚r〛2得到 6:A输出〚c〛2 加密方案转换协议中,E1,E2是两种不同的加密方案,A通过E1对随机数r进行加密,为〚c〛1添加噪音〚r〛1,将处理后的〚c′〛1发送给B,B解密后无法获取c的真实值,保证了该值在解密-再加密过程中数据的安全性,其中,r是A,B共享,M表示E1的信息空间.B通过E2对c′重新加密,将〚c′〛2发送给A,A去除噪音,得到E2加密的真实值〚c〛2,实现了从加密方案E1到E2的转换.整个加密方案转换过程中,密文噪音并未增加,且中间解密时数据真实值亦无法获取,因此,密文数据在加密转换协议中是安全的.根据本文的应用需求,设置加密方案E1是FHE,加密方案E2是Paillier,通过协议3 实现了从FHE 向Paillier 加密方案的转换. 本文的加密方案都是对整型数据进行加密,而原始数据中部分为浮点型数据,因此对数据进行处理前,需将浮点型数据转换为整型数据,处理方法是用一个足够大的常量K乘以浮点数.下面详细描述浮点数的处理过程: 首先,将浮点数据表示为IEEE 754 双精度浮点数格式,即V=(-1)s⋅M⋅2E-1023,其中,S为符号位占1 比特,M为尾数,二进制表示为(M)2=1.d,占52 比特位,1≤M≤2,M可重新表示为 其次,寻找合适的常量K,使得K满足: 令e*=miniei,δi=ei-e*≥0,则 •首先,加密方案的明文空间大于252,,因此数据转换过程中不存在空间溢出和精度损失. •其次,kNN 分类器具有的基本操作只有加法、乘法和比较,因此对转换后的数据进行操作仍能得到相同的分类结果. •最后,在执行加、乘、比较操作时,为确保操作不会造成密文数据的精度丢失,需要设置计算和比较所需的比特位数.以比较协议为例:令d表示输入数据x的属性个数,则比较时所需的最大比特位数为lmax=d+1+(52+δ*),其中,δ*=maxδi,1 表示类别标识,52+δ*表示密文数据的二进制位数.因此,比较协议中比较位数必须大于lmax.此外,还要确保,其中,λ为安全系数,N为Paillier 加密方案明文空间的模量.为了获得高安全性,设≥1 024,即λ=100. 本文训练集和测试集分别用Y和X表示,其中,xi表示第i个训练样本,则转换后的数据表示为 其中,j表示样本xi的第j个特征值. 本节利用第3 节的协议来构造PP-kNN 分类器,构造过程如下. 首先,将训练数据的类型由浮点数转换为整数,使用FHE 对其加密;其次,通过协议2 计算测试样本与所有训练样本的欧式距离,结果是FHE 加密的密文数据.然后,通过协议3 将结果转换为Paillier 加密的密文数据,再通过getMINn得到距离数组中的最小值.其思想为:先将数组中的值两两比较,得到两个中较小的值,将较大的赋值为0,较小的值的下标记为两者下标中较小方的下标值,所有较小方组成新的数组.然后继续比较新的数组,直到数组个数为1,该值即为最小值.其比较通过协议1 实现,每次比较得到一个最小值,然后将最小值重新赋值为最大值.循环k次,得出k近邻样本.最后,使用第4.2.1 节中介绍的方法来统计类别个数,得出分类结果.其中,将每个协议看作一个模块,通过模块化顺序组合进行模块衔接,构造PP-kNN 分类器,使得客户端只能获知最后的分类结果,而不能知道测试样本与训练样本间的距离;使服务器无法获取客户端的输入x(x是测试样本的向量表示). 4.2.1 PP-kNN 分类器的近邻样本类别个数统计 计算测试样本x=(x1,…,xd)与训练样本yi=(yi1,…,yid)的距离d(xi,yi),通过比较进行排序,获取前k个训练样本对应的分类标签. 设N={y1,…,yk}表示包含k个训练样本的数据集,则x对应的分类其中,L=(c1,…,cm)是所有标记的集合,I(⋅)是用来获取k个样本所属分类的函数,执行情况如下. 按上述步骤完成对k个样本所属分类个数的统计,类别个数最多的分类即为待测样本的预测分类cx. 4.2.2 PP-kNN 分类器的分类过程 kNN 分类器由服务器端与客户端两部分组成,其处理的数据是通过FHE 加密的密文数据,PP-kNN 分类器,其实质是将kNN 分类器针对明文数据的基本计算用第3 节中的安全协议替换,使kNN 分类器在分类过程中对密文数据进行操作,保证数据在分类过程中的安全性与同态性,最后得出分类结果.协议4 是对PP-kNN 分类协议的描述. 协议4.PP-kNN 分类协议. C输入:测试样本x=(x1,x2,…,xd)∈ℤd,公钥PKP,PKFHE,私钥SKQR.. S端输入:私钥SKP,SKFHE,公钥PKQR,训练集D=(y1,…,ym),标记L=(c1,…,cm),近邻数k. C输出:下标i,ci是k个近邻样本中类别个数最多的类. 1:S提供训练集D,对训练集中的训练样本进行浮点数到整数的类型转换,然后通过FHE 加密方案对训练样本进行加密 2:S将加密的〚[D]〛和近邻数k发送给C 3:设样本容量为m,for 1≤i≤m,C通过点积协议计算测试样本与训练样本的距离〚d(xi,yi)〛其中,,取结果的平方存放到数组dis_fhe中 4:C,S通过加密方案转换协议将FHE 转换为Paillier 加密方案,存入dis_paillier中 5:C:for 0≤M (1)C和S通过getMINn获取数组dis_paillier中的最小值min,并将其存入队列queue 中 (2)将min 对应的值重新赋值为最大值 6:C和S通过第5 步得到k个近邻样本〚d0〛〚d1〛…〚dk〛 7:统计k个近邻样本的类别数目,然后得到类别最多的类ci 4.2.3 安全性分析 由于点积协议、方案转换协议、比较协议在半诚实模型下是安全的,模块化线性组合在半诚实模型下也是安全的,因此,通过模块化线性组合对点积协议、方案转换协议、比较协议进行组合构造的PP-kNN 分类器也是安全的. •首先,点积协议在半诚实模型下是安全的.在通过点积协议计算测试样本与训练样本间距离时,服务器仅发送加密后的密文数据给客户端,未接收来自客户端的任何输入,保证了客户端输入数据x的安全性.客户端不拥有私钥,无法解密来自服务器的输入数据;又因为FHE 加密方案的加法、乘法同态性,保证计算过程的安全性,因此,距离计算时是安全的. •然后,加密方案转换协议在半诚实模型下是安全的.距离数据增加噪音干扰后发送给服务器,保证其解密再加密过程无法获知距离的真实值,因此不会推测出x的值;重新加密后,发送回客户端,客户端不具有Paillier 私钥,无法解密.因此,加密方案转换过程是安全的. •最后,比较协议在半诚实模型下是安全的,因此调用比较协议获取最小值的运算过程中数据也是安全的,又因为模块化顺序组合在半诚实模型下是安全的. 综上所述,通过模块化顺序组合将点积协议、加密方案转换协议、比较协议进行组合构造的PP-kNN 分类器也是安全的. 本文利用自定义加密数据对比较协议和加密方案转换协议进行性能评估,利用4 种UCI 数据集[30]对PP-kNN 分类器的性能进行评估. 测试环境具体描述如下:CPU 为英特尔酷睿i7 处理器(双核,3.4GHz);内存为16GB. 实验在相同的网络下进行,因此,本文将一个数据包的往返时间记为40ms 来模拟网络延迟.加密方案中的密钥长度为1 024 位,统计安全参数λ=100. 首先,针对两种比特长度的加密数据,从客户端、服务器运行时间、交换数据量、交换次数这4 个方面对比较协议进行了评估,实验结果见表3. Table 3 Evaluation of comparison protocol表3 比较协议评估 然后,分别对64 位、128 位、256 位、512 位、1 024 位比较比特长度的加密数据进行评估,如图1 所示. Fig.1 Performance of comparison protocol图1 比较协议性能 表3 的实验结果表明,比较协议的运行时间与比较比特长度有关,比特长度越长,服务器和客户机运行时间越长,交换数据量越多. 本节实验在Iris、Wine、Zoo、Glass Identification 公共数据集上进行测试.这些数据集是UCI 标准数据集[30],见表4. Table 4 Standard dataset表4 标准数据集 测试数据与训练数据都是按一定比例随机进行抽取,各训练样本数见表4,样本集中剩余样本作为测试集.本实验从客户端和服务端各自的计算、比较时间、交换数据总量及交换次数这几个方面进行评估,具体实验结果见表5. Table 5 Performance of PP-kNN classifier based on different test encrypted datasets表5 基于不同测试加密数据的PP-kNN 分类器性能 表5 的实验结果表明,PP-kNN 分类器的运行时间在几秒到几十秒不等,执行时间随着训练样本数与特征数的增加而增加.与贝叶斯分类器、线性分类器不同,kNN 分类器在训练阶段的消耗为0,其计算全部集中在分类阶段,因此在密文数据处理的速度方面具有一定优势. PP-kNN 中的基本操作协议都是两方协议,并且支持当前典型两方协议(TASTY[31]、Fairplay[32,33])所支持的全部功能,为了进一步说明PP-kNN 的性能优势,将本文中的比较协议与TASTY 进行比对. 本文基于不同比特位数的数据设置相应的比较位数,对TASTY 安全两方计算工具中的两方比较协议进行了性能测试,实验结果如图2 所示.TASTY 与本文的比较操作都是基于Garble 电路的,但TASTY 的数据传输消耗时间长,本文的数据传送时间较短,因此安全两方比较协议总的运行时间约为TASTY 的1/100.综上所述,本文的两方比较协议在性能上有所提高. Fig.2 Secure two-party comparison protocol runtime distribution of Tasty and ours图2 Tasty 和本文的安全两方比较协议运行时间分布 本文设计了一种支持隐私保护的kNN 分类器.首先,从kNN 分类器中提取出了一些基本操作,包括加法、乘法、比较等;其次,选择了两种同态加密方案和一种全同态加密方案对数据进行加密,基于此,设计了针对基本操作的安全协议,并证明了协议在半诚实模型下的安全性;然后,通过将基本操作的安全协议按照模块化顺序组合的方式构造出了PP-kNN 分类器;最后,在自定义加密数据及4 种UCI 标准数据集上,分别对安全协议及所构造的PP-kNN 分类器进行了性能评估.实验结果表明,本文设计的安全协议是安全且高效的,分类器能够以较高的效率对密文数据进行分类,同时实现了对用户数据的隐私保护.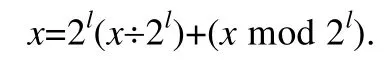







3.3 点积协议
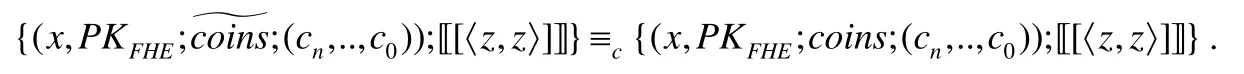
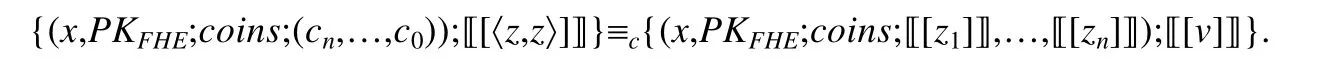

3.4 加密方案转换协议
4 PP-kNN 分类器构造及分类过程
4.1 浮点数据处理
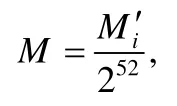
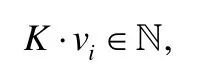

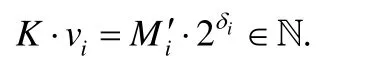

4.2 PP-kNN分类器的构造过程

5 实 验
5.1 比较协议的性能评估

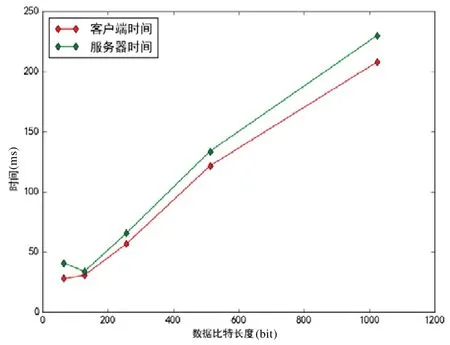
5.2 kNN分类器性能评估


5.3 安全两方工具比较协议评估与对比
6 结 论
