半球谐振陀螺全角模式控制技术研究
2019-12-11赵万良李绍良成宇翔宋丽君
赵万良,杨 浩,王 伟,李绍良,成宇翔,宋丽君
(1.南京理工大学,南京 210094;2上海航天控制技术研究所,上海 201109;3.上海惯性工程技术研究中心,上海 201109;4.西安建筑科技大学,西安 710055)
0 引言
半球谐振陀螺(Hemispherical Resonator Gyroscope, HRG)是一种高精度、高可靠性、长寿命的惯导级固体陀螺仪,通常由熔融石英谐振子、检测基座和激励罩三部分组成。它是利用半球谐振子的振动驻波(振动频率通常为4000~8000Hz)进动效应来感测陀螺载体旋转的一种振动陀螺,目前已在航天、航海、战术等领域获得了广泛的应用[1-4]。根据测量角速度或者角度,半球谐振陀螺可分为力平衡和全角两种工作模式。全角模式是一种新型半球谐振陀螺工作模式,在该工作模式下,谐振子上的振动驻波像傅科摆一样自由进动,驻波的进动角θ与陀螺载体的转动角φ呈严格的比例关系
θ=kφ
其中,k表示进动因子。
工作在全角模式下的半球谐振陀螺有以下技术特点:首先能够直接对转动角度进行测量,可有效减小由角速度随机游走带来的测量误差积累;其次由于无需力平衡作用抵消角速度引起的进动,理论上具有无限的检测带宽和动态范围;另外由于进动因子仅取决于谐振子结构,因此具有极高的标度因子稳定度和线性度。
但为了使谐振子的振动驻波自由进动,要求谐振子的激励方式不能绑定驻波方位,这使得全角模式下半球谐振陀螺的控制更加复杂。本文针对全角模式下半球谐振陀螺的控制理论、控制系统以及测量结果进行了介绍。
1 半球谐振陀螺全角模式控制理论
1.1 参数激励下的动力学方程
为实现全角模式半球谐振陀螺的速率积分功能,使谐振子驻波能够自由进动,由于传统力平衡模式的位置激励会使驻波绑定,不再适用于全角模式,因而须对谐振子采用参数激励方式。为便于计算,采用环形模型进行介绍。设参数激励电压为V=V0cosωt,则参数激励条件下,环形模型谐振子的二阶动力学方程为
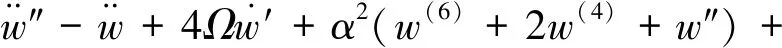
(1)
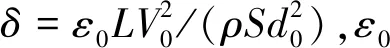
w(φ,t)=x(t)cos2φ+y(t)sin2φ
(2)
将式(2)代入方程式(1)中,并使用布勃诺夫-加廖尔金法,得到方程组为
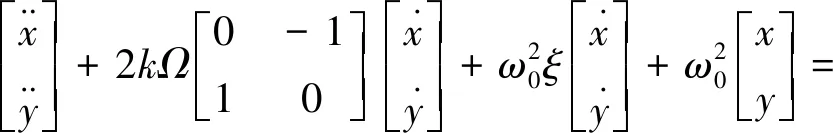
(3)
其中,Ω为载体平台转动速度,k为谐振子进动因子,对于环形模型k=0.4,ω0为陀螺谐振子固有振动频率,x和y为2个相互正交的信号轴向上的振动信号。在半球谐振陀螺中,x和y的几何放置位置相差45°。方程式(3)的解可以写为[5-8]
(4)
得出慢变量P、A、Q、B的演化方程为
(5)
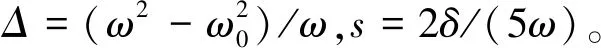
1.2 参数激励下的稳定边界条件
为使谐振子能够存在有限的稳定振动,要求
(6)
即
(7)
式(7)即确定了参数激励下谐振子的稳定边界条件。
如图1所示,在双曲线内的区域Ⅰ上,谐振子振动理想条件下将无限增长;在双曲线外的区域Ⅱ上,谐振子振动将逐渐衰减;当且仅当激励参数在稳定边界上时,谐振子的振动能够稳定。为使激励电压达到最小值,此时激励参数应满足以下条件
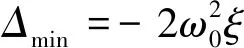
(8)
即对应的激励频率和激励电压分别为
(9)
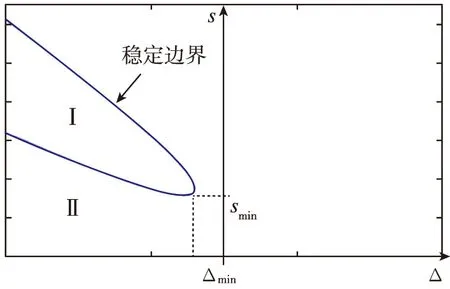
图1 参数激励的谐振子振动稳定边界Fig.1 Parameter excited harmonic oscillator vibration stability boundary
2 控制理论分析与仿真
2.1 驻波进动分析
在式(9)的激励条件下,方程式(5)化为
(10)
谐振子的振动可以写成如下形式
w(φ,t)=x(t)cos2φ+y(t)sin2φ=(Acosωt+Psinωt)cos2φ+(Bcosωt+Qsinωt)sin2φ
若ϑ表示驻波方位,则驻波方位角的变化为
利用方程式(10),得到
(11)
或对式(11)进行积分后,有

(12)
可以看出,当有角速度输入时,驻波方位的转角与陀螺壳体的转角成比例,此时半球谐振陀螺将工作在全角模式下,谐振子驻波自由进动,实现了对壳体转角的直接敏感。
若存在阻尼不均匀性时,进动方程式(9)变为[9]
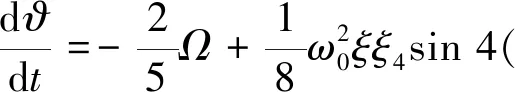
(13)
式中,ξ4为阻尼不均匀性的幅值,φ4为阻尼不均匀的方位。
2.2 控制效果分析
对上述理论进行仿真分析,当未进行参数激励与正交控制时,半球陀螺仪的x路与y路的信号输出仿真结果如图2(a)所示,此时谐振子的总能量在衰减,且正交分量随着时间出现振荡,此时陀螺仪将引入较大的零位漂移和测量误差。在按照式(9)进行参数激励后,进行正交控制,仿真结果如图2(b)所示,可以看出,谐振子总能量逐渐趋于稳定,正交分量的增长被抑制。
图2(c)所示为转速为300(°)/s时,振型方位角的进动仿真结果,表明参数激励条件下,有角速度输入时,谐振子的振型方位角处于自由进动状态,且振型方位角与外界输入角速度为严格线性关系,因而陀螺仪工作在全角模式。图2(d)所示为存在有Q值不均匀性时,陀螺仪的角度解算误差仿真结果。可以看出,解算误差随着振型方位呈周期性变化,变化周期为90°。
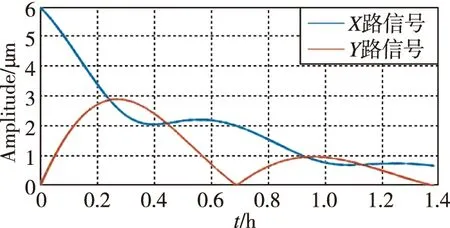
(a) 无能量补偿及正交控制时,X路与Y路信号幅值输出

(b) 有能量补偿及正交控制时,X路与Y路信号幅值输出
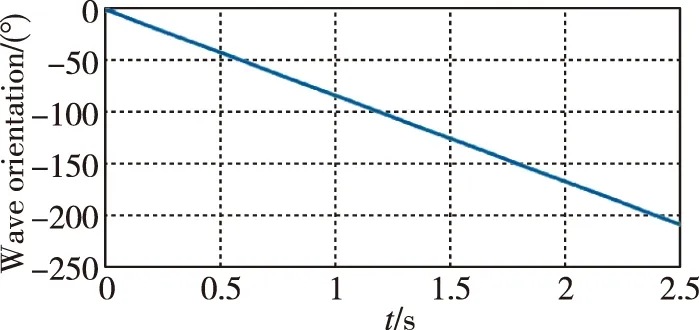
(c) 300(°)/s转速下振型进动
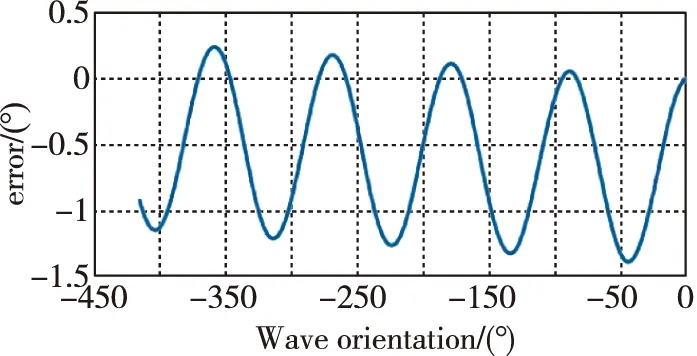
(d) 300(°)/s转速下Q值不均匀引入的解算误差
3 半球谐振陀螺全角模式控制方案
为生成所需要的控制信号,利用参考信号对检测信号X、Y通过乘法相干解调后,分别得到振型参数Cx、Cy、Sx、Sy,利用Cx、Cy、Sx、Sy进行组合运算,得到所需要的控制判断量,分别为[10]
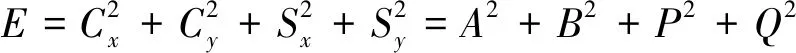
(14)
则E表征当前谐振子振动的总能量,该值与设定幅值E0的差值形成能量控制误差信号,用于对幅度的控制;Q表征陀螺振动模态正交误差量的大小,用于对正交误差的控制;L用于实现对谐振子频率的跟踪;S、R表征振型方位,且振型方位角为
(15)
形成控制量以后,将控制量与判断量进行比较,并按照式(9)进行驱动合成和调制,进而生成控制电压,作用到半球谐振陀螺的控制电极上,实现对半球谐振陀螺的参数激励控制,如图3所示。

图3 基于参数激励的全角模式控制方案[11]Fig.3 Whole-angle mode control scheme based on parameter excitation
4 实验
4.1 实验装置
利用第3节所述算法设计硬件系统并加以实现。全角模式半球谐振陀螺系统的硬件结构由信号检测硬件接口、驱动输出硬件接口、基于FPGA的数字硬件系统以及辅助外围电路组成。其中信号检测硬件接口和驱动输出硬件接口两部分属于模拟电路系统,用于实现系统与陀螺表头之间的信号交互;基于FPGA的数字硬件系统为数字电路系统,用于实现陀螺工作流程的控制、数字信号处理与控制算法实现以及外设通信接口功能;辅助配套电路包括电源模块、通信芯片、保护隔离器件等。硬件系统的实物图如图4所示。

图4 全角模式半球谐振陀螺硬件电路系统Fig.4 Whole-angle mode hemispherical resonator gyro hardware circuit system
FPGA是全角模式半球谐振陀螺信号处理与控制算法的载体与核心。本课题选用Xilinx公司ARTIX系列第7代FPGA产品xc7a35t,在该器件的基础上实现了陀螺系统的信号运算、控制与信号交互。FPGA数字系统的功能组成结构图如图5所示。
4.2 实验结果及分析
图6所示为全角模式半球谐振陀螺实验结果。图6(a)表明能量逐渐收敛到3.2×105bit,表明在参数激励作用下,控制系统实现了对谐振子振动能量的控制。在能量达到稳定后,使转台转速为300(°)/s,陀螺仪的振型方位变化如图6(b)所示,由于三角函数求解时,角度输出随时间呈锯齿变化。对测量的振型方位角进行线性化,并对转台转速稳定后的数据进行线性拟合,得到图6(c),表明在大动态角速度输入下,陀螺仪在0°~360°范围内实现了对旋转角度的实时敏感,拟合后的结果为
θ=-0.275φ+182.1
(16)
拟合线性相关系数大于0.9999。因此该陀螺的进动因子为0.275,与基于环形模型的理论进动因子0.4相比误差较大,与基于半球壳模型的理论进动因子0.277基本一致[12-13],线性度优于10-4。图6(d)所示为不同振型方位下的转动角度解算误差量,解算误差量随着方位角做周期性变化,变化周期为90°,由仿真结果可知,该误差是由阻尼不均匀引起的。
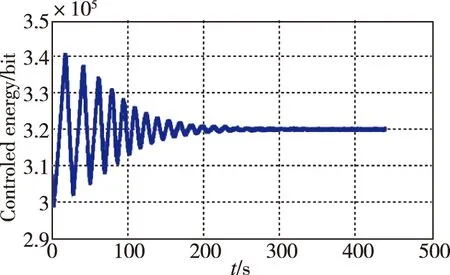
(a) 能量收敛过程
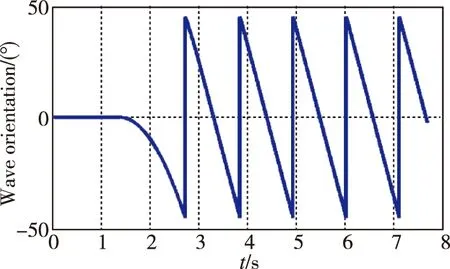
(b) 转速300(°)/s振型方位变化情况
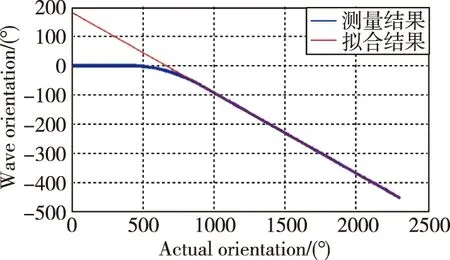
(c) 实际转动角度与振型方位角的关系
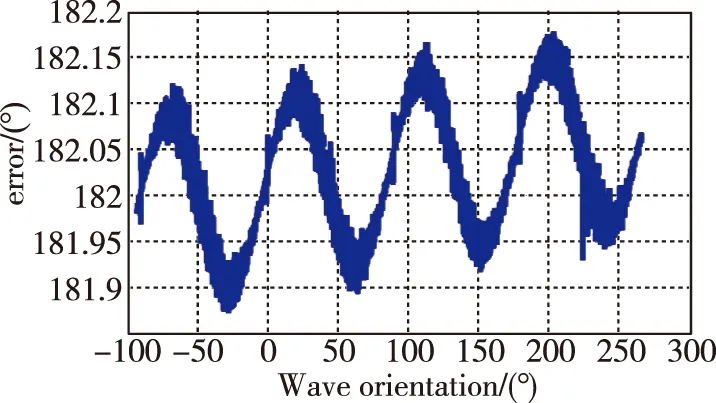
(d) 不同振型方位角下的解算误差
5 结论
本文研究了全角模式半球谐振陀螺,介绍了全角模式半球谐振陀螺的基本理论,并利用参数激励的方法实现了半球谐振陀螺全角模式的测量功能。测试结果表明,测量角速度可达300(°)/s,线性度优于10-4,后续将需着力于漂移抑制以及控制系统性能的提升。
