交通流数据自适应特征选择算法

邓 晶，张 倩

(南京工程学院 计算机学院，江苏 南京 211167)

0 引 言

随着交通规模的不断扩大，影响交通状态的因素也越来越多。从复杂的交通影响因子中选择出有效的特征作为交通流预测模型的数据输入，对提高交通预测系统的准确性有着重要的作用[1]。决策树算法在分裂形成决策树的过程中，天然地对特征进行了选择，但单棵的决策树很不稳定，且仅仅只能对特征重要度进行计算，并不能直接选择出合适的特征集合。因此，把集成学习方法和决策树算法相结合，提出一种基于梯度提升决策树的自适应特征选择方法。其中迭代生成的若干决策树综合计算得出了特征的重要度，解决了单棵决策树的局限性，通过二次下降法选择合适特征，实现对高维度交通流数据的自适应选取。

1 数据清洗与数据规范化

交通数据采集的途径和方法有很多。在采集过程中不可避免的会产生一些问题。假如不对原始采集数据进行预处理，检查并清除问题数据，妥善处理好缺失值和异常值，必然会使研究结果产生很大偏差。

牛顿插值法处理结构复杂的多项式时，计算量相对较少，且对于数据的拟合程度较好[2]。因此，文中采用牛顿插值法对缺失数据进行补值计算。以5分钟作为一个时间间隔，如把0：00的数据作为开始点，每隔5分钟对数据进行搜索，如在某个时间点搜索到的数据为空，将这个时间点的数据视为数据缺失。

噪声数据是指原始数据中由于某些原因引起的错误变化。如天气因素、交通事故等。小波去噪对于处理非平稳的、非线性的数据具有很好的效果[3]。交通流数据异常一般是指在某个局部范围内出现与总体不一致的变化。如果选用合适的小波函数对数据进行一定尺度的小波变换，通过信号重构，去掉噪声数据[4]。

数据规范化是数据挖掘过程中的一项基本操作，考虑到交通数据的特点，采用0均值标准化对数据进行归一化处理。

2 特征重要度计算

特征选择是从已知的特征集合中选择一个子集，该子集可以全面有效地对数据进行描述，后续的预测分析工作可以针对该子集进行。选择出优良的特征数据，不仅可以降低数据计算量，提升效率，而且可以帮助研究者更深入地理解研究对象[5]。

2.1 单棵CART树中特征的基尼指数和分裂次数

决策树算法在生成树的过程中，天然需要对特征进行选择，其训练过程本身就是对特征进行选择的过程[6]。CART决策树作为基学习器，在分类与回归过程中计算出每棵树的基尼指数以选择最优特征，同时确定该特征的最优二值分割点，从决策树的根节点开始依次选择能使分割后样本集基尼指数最小的特征和值。

对于给定的一个样本D，假设确定类别个数，其基尼指数可以定义为[7]：

(1)

其中，N是类别个数；cn是N中属于第n个类的样本数量。

如果样本D根据特征F的某个值f，其被分隔成D1和D2两部分，则在特征F的条件下，样本D的基尼指数可以定义为：

(2)

建立CART分类树以及计算每个特征的基尼指数和分裂次数的伪代码如下所示：

算法：CART分类树算法伪代码。

输入：训练特征数据集D，基尼指数的阈值th2，样本个数的阈值th1；

输出：决策树Tree，每个特征的基尼指数数组gini_list[]，每个特征的分裂次数K。

输入特征数据集D

Tree(data)从根节点开始，递归训练集建立决策树

If样本数小于阈值th1或没有特征then

return返回决策子树，停止递归

计算基尼指数

If基尼指数小于阈值th2then

return返回决策子树，停止递归

fori=1 toN

计算当前节点现有的各个特征的特征值对数据集D的基尼指数gini_fecture[i]

存储计算结果gini_list[]=gini_fecture[i]

End for

选择基尼指数最小的特征F和对应的特征值f

根据这个最小的特征F和对应的特征值f，划分数据生成两部分

建立当前节点的左右节点，左节点的数据集D为D1，右节点的数据集D为D2

对左右的子节点进行递归调用，生成决策树

计算所有特征的分裂次数K

Return Tree(data)

CART回归树和分类树的建立算法大致相同，主要区别在于：连续值的处理方式不同；决策树建立后做的预测方式不同。对于连续值的处理，CART回归树采用了方差的度量方式[8]。CART回归树的度量目标是，对于任意划分特征A，对应的划分点S两边划分成数据集D1和D2，求出使D1和D2各自集合的均方差最小，及其所对应的特征和特征值划分点。对于决策树建立后做的预测方式，CART回归树输出的不是类别，它采用的是最终叶子的均值或者中位数来预测输出结果。

2.2 梯度提升决策树(GBDT)模型

梯度提升决策树(GBDT)是一种迭代的决策树算法。它通过构造一组弱学习器，即多个单棵CART树，并把这些弱学习器的结果累加起来作为最终的预测输出[9]。每个分类器在上一轮分类器的残差基础上进行训练。训练过程是通过降低偏差来不断提高最终分类器的精度。其模型可表示为：

(3)

其中，M为CART树的个数；fm(x)为决策树，通过拟合损失函数的负梯度得到[10]。

算法中需要利用回归树对损失函数的负梯度进行拟合，有关参数如下：

设训练数据集T={(x1,y1),(x2,y2),…,(xN,yN)}，其中xi∈x∈Rn，x为输入空间，yi∈γ∈R，γ为输出空间。如果将输入空间x划分为J个互不相交的区域，即R1,R2,…,RJ，并在每个区域上确定输出的常量，那么树可以表示为：

(4)

其中，参数 ⊗ ={(R1,r1),(R2,r2),…,(Rj,rj)}，表示树的区域划分和各区域上的常数；J表示回归树的复杂度及叶子节点的个数。

单棵决策树的梯度提升算法采用的是前向分布算法。首先确定初始提升树f0(x)=0，第m步的模型为：

fm(x)=fm-1(x)+T(x,⊗m)

(5)

利用梯度提升算法使得损失函数最小，从而确定下一棵决策树的参数⊗m。

(6)

梯度提升决策树的核心伪代码如下：

算法：梯度提升决策树回归算法。

输入：训练样本集T={(x1,y1),(x2,y2),…,(xN,yN)}，最大迭代次数M以及损失函数L；

输出：强学习器f(x)。

估计使损失函数极小化的常数值，它是只有一个根节点的树

Form=1 toM

Fori=1 toNdo

计算损失函数的负梯度在当前模型的值，将它作为残差的估计

end for

估计回归树叶节点区域rim，以拟合残差的近似值Rjm，j=1，2，…，jm

Forj= 1 tojmdo

利用线性搜索估计叶节点区域的值，使损失函数极小化

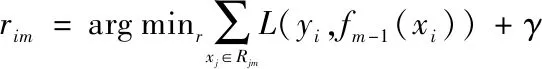
end for

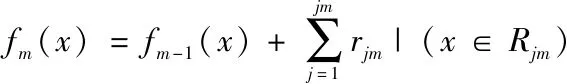
end for

得到输出的最终模型

Outputf(x)=fm(x)

3 基于梯度提升决策树的自适应选择算法

在梯度提升决策树训练完成得到最终模型后，迭代生成了M棵CART树[11]，同时计算了每个特征的基尼指数和分裂次数。因此定义每个特征xi的全局重要度I(xi)如下：

(7)

在得出特征重要度的基础上，为了能够合理地选择有效的特征集合，设计了一种二次下降法，提出了一种基于梯度提升决策树的自适应选择算法。

算法流程如下：

step1：对数据进行预处理，充分清洗原始数据，包括交通流数据的缺失处理和交通流数据去噪。

step2：采用CART作为基学习器，用GBDT算法拟合回归特征数据，迭代生成M棵CART树。在生成过程中，每棵CART树同时进行了分类与回归。分类是为了计算出每个特征在每棵CART树中的基尼指数和分裂次数，回归是为了GBDT算法的迭代回归拟合生成决策树。

step3：根据基尼指数和分裂次数的组合来计算每个特征的重要度，并进行归一化处理，生成特征重要度集合L。

step4：建立一个特征子集。

step5：选择重要度最大的特征为特征子集元素。在特征总集合L中删除已选特征，并更新特征子集。

step6：计算特征子集进行预测的拟合回归准确率P。如果Pn>Pn+1>Pn+2，则转至步骤7，否则返回步骤5。

step7：输出特征子集。

如上所述，如果连续两次加入次重要的特征进入特征子集后，预测准确率都不会提高，则结束算法，输出选择后的有效特征集合，此为二次下降法。

4 实验结果和分析

4.1 数据来源与评价指标

实验数据来源于美国加州交通局的PEMS系统。PEMS系统的数据是开源的，用于各类研究者学习和使用。在PEMS系统中，随机选取一个时段的数据。该段数据已经被处理成5分钟一个间隔的交通流数据，包括车辆流数、车速及车道占有率等。另外，引入天气因子，对天气情况特征做出说明；引入时间类别，对普通工作日、节假日、重大节日等进行区分。

文中的最终目的是进行准确的交通流数据特征选择，为此引入了广泛应用于回归问题的评价指标，分别为平均绝对百分比误差(MAPE)和均方根误差(RMSE)[12]。其中，MAPE表征了预测值偏离实际值的程度。MAPE越小，表明预测值越接近于实际值，预测效果越好。RMSE表征了误差大小以及误差分布的离散程度。RMSE越小，误差离散程度越低，预测效果也就越好[13]。

4.2 实验一：数据清洗

为了测试牛顿插值法的效果，选取了标号为I-80W公路的某路段在2017年12月22日8:00-21:00的交通流数据。预先删除了原始数据中8:10、10:35、12:00、14:15、17:45、20:50这六个时间点的交通流数据，然后使用牛顿插值法对缺失数据进行处理，表1为使用牛顿插值法后的插补结果对比。

表1 牛顿插值法结果对比

从表中可见，经过插补后的数据与原始数据拟合良好，可以达到缺失数据补全的要求。

4.3 实验二：基于梯度提升决策树的自适应特征选择

为了验证文中算法的有效性，选取了随机森林的特征选择算法和基于CART决策树的特征选择算法与文中的梯度提升决策树算法进行对比。

首先，对数据进行清洗和去噪。之后选取编号为11、12、13的三个路段从2017年12月14日到12月20日之间的交通流数据；编号14路段作为预测路段。以此构造特征变量集合。其中，ch1到ch21共21个特征，包括编号14预测路段现在、五分钟前、十分钟前的交通流量，编号11到13路段现在、五分钟前、十分钟前的交通流量，编号11到14路段现在车道的平均占有率，以及天气状态和节假日状态。将该特征集作为原始训练数据集，应用于文中的特征选择算法和对比的算法模型中。

表2显示了梯度提升决策树的特征选择算法和其它两种算法对数据进行特征选择后的结果。

使用三种算法选出的特征分别构造训练集和测试集，分别将其放入ARIMA模型、BP神经网络模型和支持向量机模型进行交通流预测。使用MAPE指标和RMSE指标对预测结果进行评判，得到的结果如表3和表4所示。

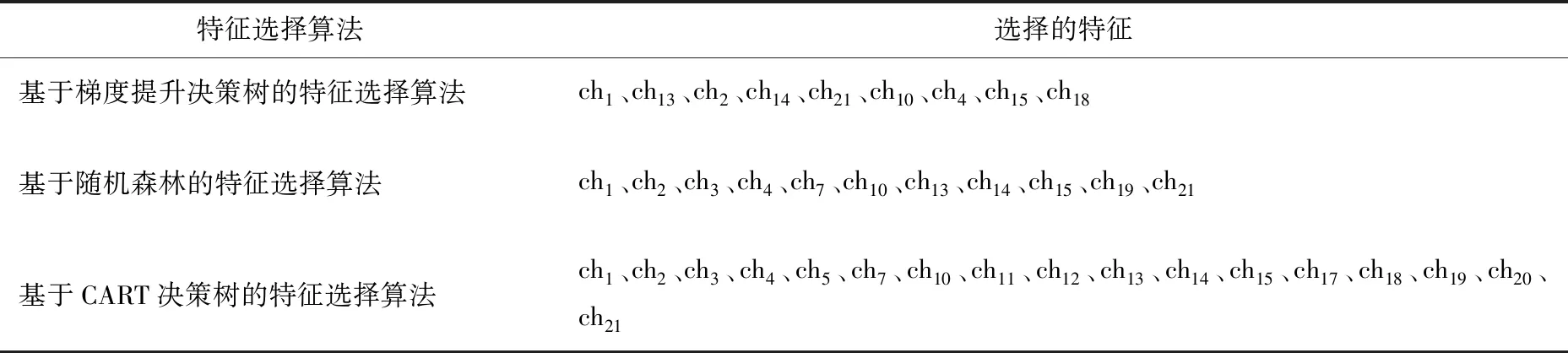
表2 特征选择结果

表3 特征选择的RMSE效果对比

表4 特征选择的MAPE效果对比

从表3中可以看出，在对特征集进行提取前后，RMSE值的区别都很明显。即使是在三种算法中特征选取效果较差的CART决策树算法，相对于未经选择的原始特征，预测模型的RMSE值也有明显下降。而使用梯度提升决策树自适应算法的RMSE值最低，预测效果更明显。从表4中看出，MAPE的变化情况和RSME的类似。综上，在进行交通流预测之前进行特征选取是很必要的[14]。而文中提出的基于梯度提升决策树的自适应特征选择算法相较于其他两种算法，性能有明显提升，能够选取出更好的特征组合，实现对数据更好的描述，最终使得交通流预测模型的预测精度更高。

5 结束语

使用梯度提升决策树自适应特征选择算法对交通流数据进行特征选择，为实时交通流预测模型提供训练数据集。经实验对比，文中算法优于传统的特征选择算法。由于时间和水平有限，文中的研究内容有待于进一步拓展。主要有以下几点：由于影响交通流的因素很多，只考虑了其中重要的若干因素，需要将更多的影响因子加入到模型中；梯度提升决策树通过不断迭代弱学习器生成强学习器[15]。由于弱学习器之间存在依赖关系，难以并行训练数据。因此耗费时间较长。接下来应进一步研究如何优化学习过程，以期满足交通流预测的实时性。