三角形内角和180°该如何说明

章勤琼 杜娅茹

【摘   要】推理一般包括合情推理和演绎推理，合情推理用于探索思路，发现结论;演绎推理用于证明结论。“三角形的内角和”这一内容是培养学生推理能力的重要内容，但在现实教学中，不论是合情推理或是演绎推理，都存在一些问题。在推理能力的培养中，需要注意以下两点：第一，关注学生的真实起点，培养良好的思维习惯，真正将培养学生的推理能力落到教学实处;第二，处理好合情推理和演绎推理的关系。

【关键词】三角形;内角和;合情推理;演绎推理

推理能力属于《义务教育数学课程标准（2011年版）》中的十大核心概念之一，也是《普通高中数学课程标准（2017年版）》中明确提出的六大数学核心素养之一。推理是形式逻辑术语，是一种重要的思维形式，即由一个或几个已知命题推出一个新命题的思维形式。[1]推理在人们认识客观世界的过程中发挥着巨大的作用，要推理出正确的结论，需要有两个条件，一是推理前提是真判断，二是推理形式正确。[2]因此，只要推理前提为真，推理过程正确，结论就一定正确。

“三角形的内角和”是小学阶段“图形与几何”领域一节很有代表性的经典课例。从数学内容来看，边和角是三角形的重要属性，属于必须掌握的重要知识。更重要的是，这一内容对于学生推理能力的培养有着非常重要的价值。教材通过“量角”“拼角”和“折角”等方式，让学生经历说明三角形内角和是180°的过程，这是一种合情推理①的方式。现在很多教师的教学中，会在上述内容之后加入演绎推理的内容。

那么，对于小学生而言，三角形的内角和是180°，应该以怎样的方式进行说明比较合适？合情推理和演绎推理在教学中又该如何落实？我们应该对相关概念进行梳理，进而对教学有进一步的思考。

一、课堂上的合情推理“合情”吗？

《义务教育数学课程标准（2011年版）》中指出，推理一般包括合情推理和演绎推理，合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果;演绎推理是从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算。在解决问题的过程中，合情推理用于探索思路，发现结论;演绎推理用于证明结论。[3]

一般来说，小学阶段应更关注学生探索与发现的过程。因此，实际教学会偏重于合情推理的内容，或者说合情推理会多于演绎推理。[4]合情推理是数学家波利亚对归纳推理、类比推理等或然性推理（即推理的结论不一定成立的推理）的特称。它是从已有的事实出发，凭借经验和直觉，通过归纳、类比等推断某些结果，是一种合乎情理、好像为真的推理。[5]

对小学生来说，三角形的内角和这个内容，有两方面的学习价值。一是知道三角形内角和是180°这个知识;二是经历探索三角形内角和并进行说明的过程。但由于学习机会的增多，三角形内角和是180°这个结论，很多学生都已经知道。在知识性的结论已经知道的情况下，这节课学生还需要获得什么？对很多教师来说，这是比较难处理的事。事实上，已经知道内角和为180°，并不影响这节课的教学，可以考虑转变教学重点，不放在探索内角和的度数上，而是在已经知道了内角和是180°的情况下，有没有办法说明为什么内角和是180°呢？

一般来说，“三角形的内角和”的教学中都会有这样几个环节，先提出问题，然后经历观察尝试、猜想、验证、一般化等过程。通常是让学生通过量角得到内角和接近180°，在此基础上提出猜想“内角和可能是180°”。接着就用多种方法进行验证，比如剪下来拼一拼或者折一折等方法，验证三个角刚好可以拼成180°。这是合情推理的过程，在猜想之后通过操作活动进行验证，得到猜想的结果为真。

那么，如果以推理的要求来看上述过程，合情推理是否真的“合情”呢？笔者在一次听课过程中，在量角验证这一环节中，看到有学生在量出了两个角分别是40°和70°后，利用180°减去这两个角后，得到第三个角为70°，随后又在求内角和的时候将这三个角相加，得到180°。1学生这样的操作当然是有问题的，这与本节课推理能力培养的目标是背道而驰的。无论哪一种推理，推理的每一步都是由作为前提的命题形式出发逐步得到作为结论的命题形式的过程。[6]也就是说，在推理的每一个步骤中，都需要清楚区分前提和结论。在本节课中，三角形的内角和是180°并不是给出的前提，而是需要证明的结论。因此，学生要有这样的意识，尽管已经知道这一知识结论，但在推理的过程中不能作为前提循环使用。这是“量”这个环节最值得注意的地方，推理的前提意识会比量角产生的误差要如何处理更值得关注。

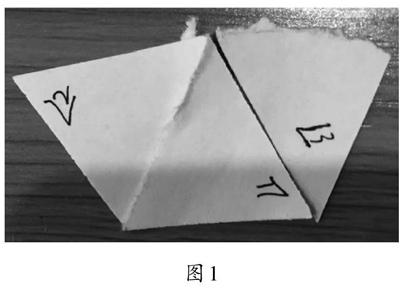
同样，在“拼角”这个环节，则需要特别关注推理的逻辑过程是否指向结论的得出。譬如，有一次在课堂上，看到学生将三角形的三个内角拼成如图1的样子。当问到这是在做什么的时候，学生说，我拼成了一条直线，是平角，是180°，所以三角形内角和是180°。很显然，学生在这里的操作只是关注了表象的180°，甚至只关注了拼成直線，却没有意识到只有将三个内角拼在一起，才能完成三角形的内角和到平角的转化，这样的推理过程才正确，才能推出正确的结果。后面“折角”的环节也类似，需要关注何为前提何为结论，也需要特别注意过程的正确性。

图1

二、课堂上的演绎推理足够严谨吗？

与合情推理并存的是，小学数学的教学内容中有很多演绎推理的内容值得进一步挖掘。[7]还是以“三角形的内角和”为例，在如今的教学中，很多教师在学生经历“量”“拼”“折”这些操作性的说明方式之后，会希望学生进行一定程度的演绎证明。一般情况下，先从直角三角形入手，引导学生把长方形沿对角线分成两个一样的直角三角形，长方形四个直角的和是360°，三角形内角和就是360°÷2=180°。在证明了直角三角形的内角和是180°之后，再证明锐角三角形和钝角三角形的内角和也是180°。

让学生进行这样演绎推理的尝试很有价值。虽然从数学的角度来看，这样的做法显然算不上严谨的演绎证明。张奠宙曾指出，从四个角都是直角的四边形出发，绕开平行公理，严格地证明“三角形内角和是180°”是错误的，也是不可能的。[8]然而，从教学的角度来看，我们更要关注学生在这个过程中能获得什么。推理教学最重要的价值是让学生形成说理与论证的意识、能力和习惯，需要关注何为前提、是否为真，逻辑过程是否正确。而且，这些推理论证的每一步过程都是基于学生的基础的，即前提和过程都是现阶段学生能理解并接受的。

因此，相比从数学上探讨这样的方式是否足够严谨，更重要的是给学生机会去思考其中的过程是否有理有据，能否接受1。譬如，长方形分成的两个直角三角形是不是完全一样，可以怎样说明？事实上，从学生的角度来看，要说明由长方形剪开得到的两个直角三角形能够完全重合并不容易。因为长方形跟正方形不一样，没法通过對折能够重叠来说明。因此，在教学中可以先由最特殊的等腰直角三角形开始，学生通过正方形对折就能得到两个完全一样的三角形。再到长方形，对折无法重合，那该如何说明两个三角形完全一样？学生需要经历尝试剪下来之后旋转重合的过程。这当然算不上严谨的演绎证明，但这样一种说服自己说服同伴的经验非常重要。在这样的基础上，下面一个问题的讨论显得尤为重要。这里只说明了这一个长方形沿着对角线分开的两个直角三角形完全一样，如何说明所有直角三角形都是180°？我们知道，因为这个长方形的选择是随意的，没有任何额外的要求，所以可代表所有情况。但这样一种“不失一般性”的思考是非常高阶的思维，对于小学生来说很难理解。因此，学生需要思考，在说明了一个直角三角形的内角和是180°后，用什么方法能说明所有直角三角形都是如此？当长方形改变时，什么变了，什么没变？学生需要关注的是，长方形的长和宽都在变化，从而直角三角形的三条边也都在变化，但两个直角三角形之间的关系没变，即将不同的长方形沿对角线剪下来后的两个三角形，旋转之后都能够重合，所以内角和仍然是360°的一半。只有到了这里，才算是真正对直角三角形内角和是180°说清楚了。

这样，直角三角形内角和是180°就可以作为证明锐角三角形和钝角三角形内角和为180°的条件。在证明锐角三角形和钝角三角形的内角和是180°时，需要更加关注从学生的经验出发，如何将这两类三角形转化为直角三角形，本文不再赘述。

三、两点教学建议

像“三角形的内角和”这样的内容的教学，应该指向培养学生的推理能力等核心概念的学习，而不仅是掌握内角和是180°这样的知识性目标，这一点应当成为教学的共识。关于推理能力的培养，需要注意以下两点。

第一，关注学生的真实起点，培养其良好的思维习惯，真正将培养学生的推理能力落到教学的实处。小学生的推理能力有两个特点，一个是天生敢想敢说，喜欢问问题，具有有利于数学猜想的心理优势;另一个是儿童思维的抽象性、逻辑性处在逐步发展的过程中，有时也会随心所欲，脱离数学事实提出想法。[9]如前文所述，小学生对于推理中前提和结论的区分就不清晰。培养推理的严谨性需从平时教学的一点一滴中做起，因此，需要培养小学生“有根有据、有条有理”的思维习惯，在推理教学中切忌蜻蜓点水、似是而非。相比在一节课上同时追求合情推理与演绎推理但又都浅尝辄止，让学生深刻理解推理中的前提和结论，充分体会前提为真、形式正确，结论才正确的过程，更为重要。

第二，处理好合情推理和演绎推理的关系。如课标中所说，合情推理和演绎推理都是推理能力的重要组成部分，对于小学生推理能力的形成都不可或缺。然而，合情推理是个相对宽泛的概念，需要对推理能力的相关概念进行进一步的厘清，如演绎推理、归纳推理、类比推理等，更重要的是，要对这些推理之间的关系进行梳理。小学数学中合情推理与演绎推理是相辅相成的，各自的作用不宜绝对化。[10]有研究者指出，如果过分强调 “合情推理模式”，从而割裂归纳推理和演绎推理的联系，则会对数学学科的教育功能造成损害。[11]事实上，如果仅仅强调“演绎推理模式”，亦是如此。此外，在小学阶段推理的教学中，常常需要用到操作的方式，但需注意处理好操作与说理的关系。[12]

参考文献：

[1] [5] [6]吴正宪， 刘劲苓，刘克臣. 小学数学教学基本概念解读[M]. 北京;教育科学出版社，2014： 28;29;28.

[2] 金成梁.小学数学疑难问题研究[M]. 南京： 江苏教育出版社，2010：238.

[3] 中华人民共和国教育部.全日制义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2011：6 - 7.

[4] [7] [9] [10]曹培英. 跨越断层，走出误区：“数学课程标准”核心词的解读与实践研究[M]. 上海： 上海教育出版社，2017：130;131;136;128.

[8] 张奠宙，巩子坤，等. 小学数学教材中的大道理——核心概念的理解与呈现[M]. 上海：上海教育出版社，2018：325 - 326.

[11] 连四清，方运加. “合情推理”辨析[J]. 课程·教材·教法，2012，32（5）：54 - 57.

[12] 游迪. 小学数学教学中的操作与说理——以圆锥的体积为例[J]. 小学教学（数学版），2018，（10）：27 - 32.

（温州大学   325035）