隐形圆中定角定高破解中考压轴面积最值（探照灯模型）

杨格瑞

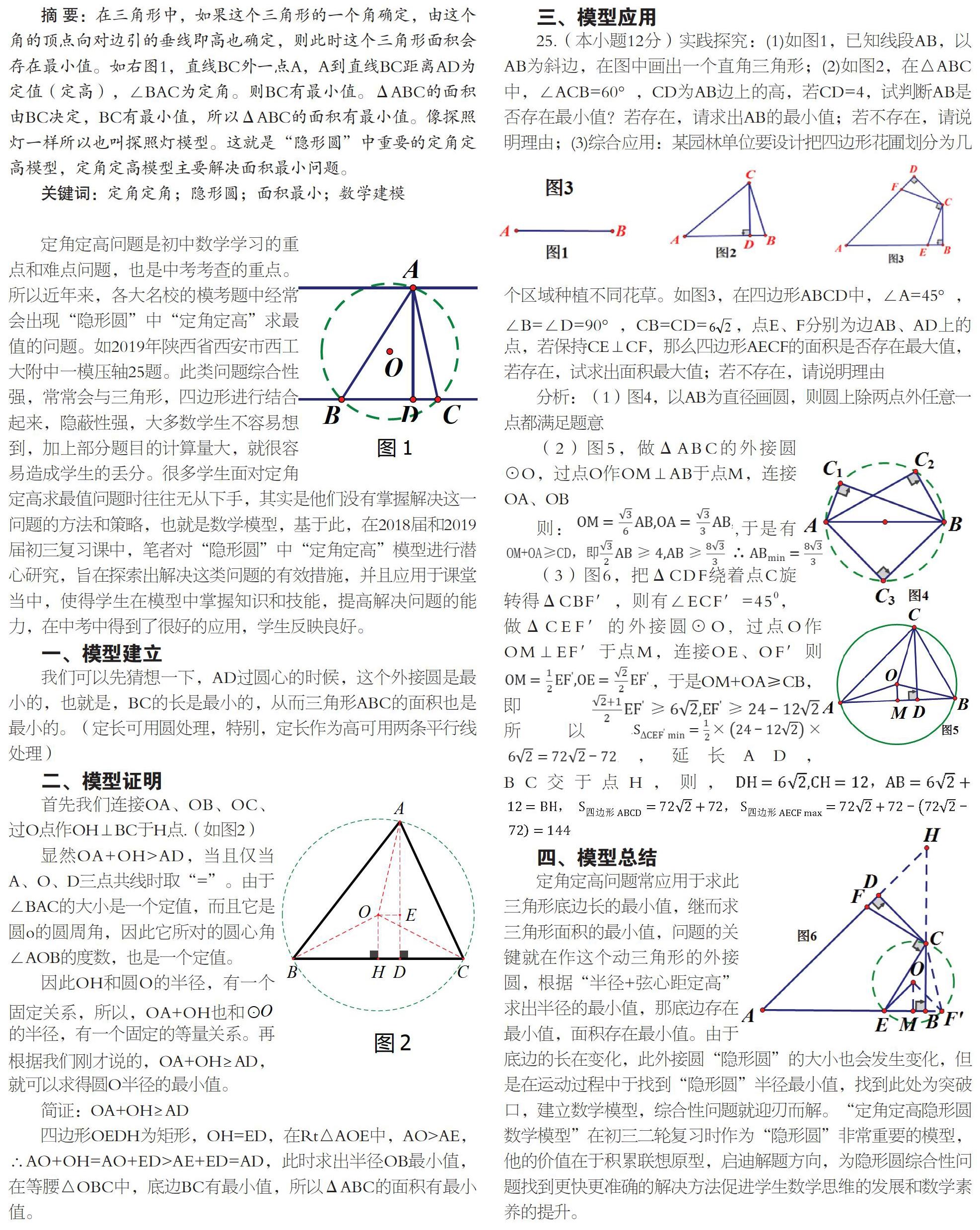
摘 要：在三角形中，如果这个三角形的一个角确定，由这个角的顶点向对边引的垂线即高也确定，则此时这个三角形面积会存在最小值。如右图1，直线BC外一点A，A到直线BC距离AD为定值（定高），∠BAC为定角。则BC有最小值。ΔABC的面积由BC决定，BC有最小值，所以ΔABC的面积有最小值。像探照灯一样所以也叫探照灯模型。这就是“隐形圆”中重要的定角定高模型，定角定高模型主要解决面积最小问题。

关键词：定角定角;隐形圆;面积最小;数学建模

定角定高问题是初中数学学习的重点和难点问题，也是中考考查的重点。所以近年来，各大名校的模考题中经常会出现“隐形圆”中“定角定高”求最值的问题。如2019年陕西省西安市西工大附中一模压轴25题。此类问题综合性强，常常会与三角形，四边形进行结合起来，隐蔽性强，大多数学生不容易想到，加上部分题目的计算量大，就很容易造成学生的丢分。很多学生面对定角定高求最值问题时往往无从下手，其实是他们没有掌握解决这一问题的方法和策略，也就是数学模型，基于此，在2018屆和2019届初三复习课中，笔者对“隐形圆”中“定角定高”模型进行潜心研究，旨在探索出解决这类问题的有效措施，并且应用于课堂当中，使得学生在模型中掌握知识和技能，提高解决问题的能力，在中考中得到了很好的应用，学生反映良好。

一、模型建立

我们可以先猜想一下，AD过圆心的时候，这个外接圆是最小的，也就是，BC的长是最小的，从而三角形ABC的面积也是最小的。（定长可用圆处理，特别，定长作为高可用两条平行线处理）

二、模型证明

四、模型总结

定角定高问题常应用于求此三角形底边长的最小值，继而求三角形面积的最小值，问题的关键就在作这个动三角形的外接圆，根据“半径+弦心距定高”求出半径的最小值，那底边存在最小值，面积存在最小值。由于底边的长在变化，此外接圆“隐形圆”的大小也会发生变化，但是在运动过程中于找到“隐形圆”半径最小值，找到此处为突破口，建立数学模型，综合性问题就迎刃而解。“定角定高隐形圆数学模型”在初三二轮复习时作为“隐形圆”非常重要的模型，他的价值在于积累联想原型，启迪解题方向，为隐形圆综合性问题找到更快更准确的解决方法促进学生数学思维的发展和数学素养的提升。