2019年高考 “空间几何体和线面位置关系中的经典问题”

■朱奕帆

本文以2019年高考题为载体,探究空间几何体和线面位置关系中经典问题的求解思维方法,希望对大家的学习有所帮助。

聚焦1：由三视图判断几何体的特征或求面积或求体积

例1(2019年高考浙江卷)祖暅是我国南北朝时期的伟大科学家。他提出的 “幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=Sh,其中S是柱体的底面积,h是柱体的高。若某柱体的三视图如图1所示,则该柱体的体积是____。

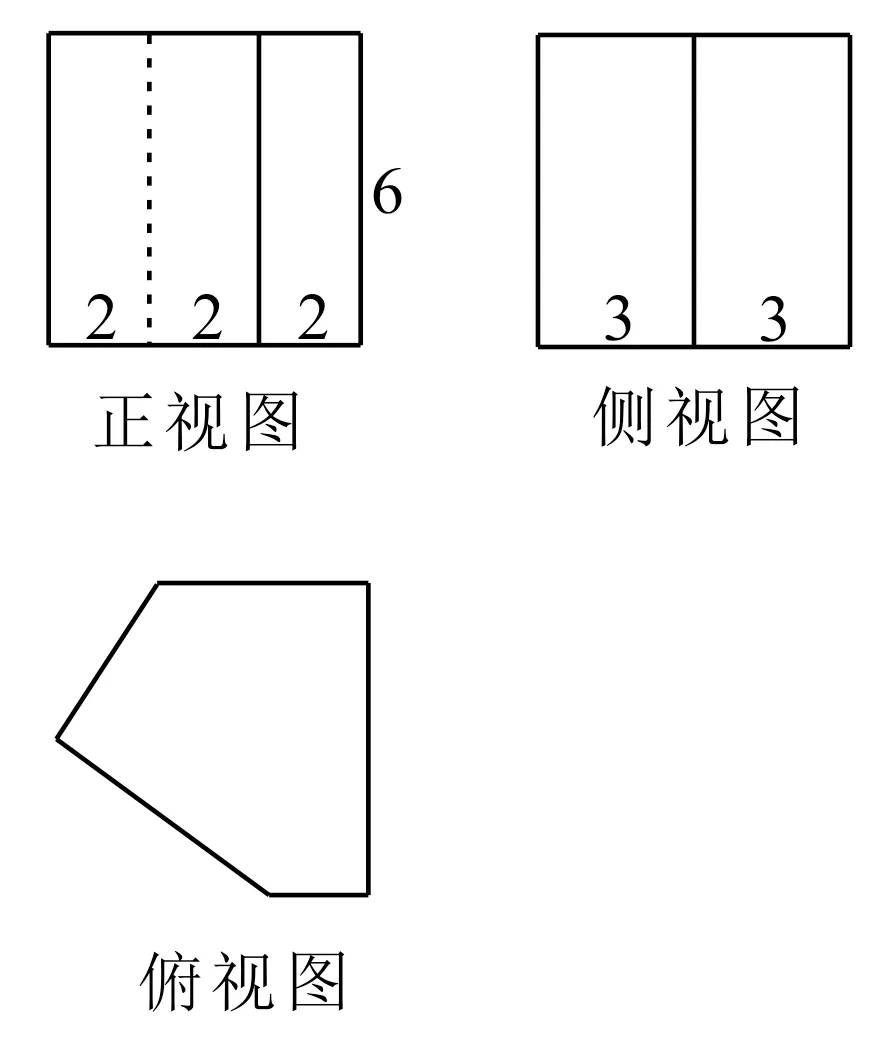
图1

解：根据三视图,可还原得到的几何体为底面是五边形的直棱柱,利用给定的数据,可计算几何体的体积。由三视图可得该棱柱的高为6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为4,下底为6,高为3,另一个上底为2,下底为6,高为3,由此可得该棱柱的体积为V=162。

回味：由三视图判断几何体的特征或求面积或求体积,关键是正确还原出直观图,在还原几何体时要利用三视图的特征:正俯一样长,俯侧一样宽,正侧一样高。

聚焦2：组合体的体积计算问题

例2(2019年高考天津卷)已知四棱锥的底面是边长为2的正方形,侧棱长均为5。若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____。

解：根据棱锥的结构特点,确定所求的圆柱的高和底面半径。由题意可知正四棱锥的高为,故圆柱的高为1,圆柱的底面半径为,可得该圆柱的体积为

回味：解答本题的关键是确定所求的圆柱的高和底面半径,同时还需要有空间想象能力。

聚焦3：平移法求异面直线所成的角

例3(2019 年高考上海卷)如图2,在正三棱锥P-ABC中,PA=PB=PC=2,AB=BC=AC= 3。

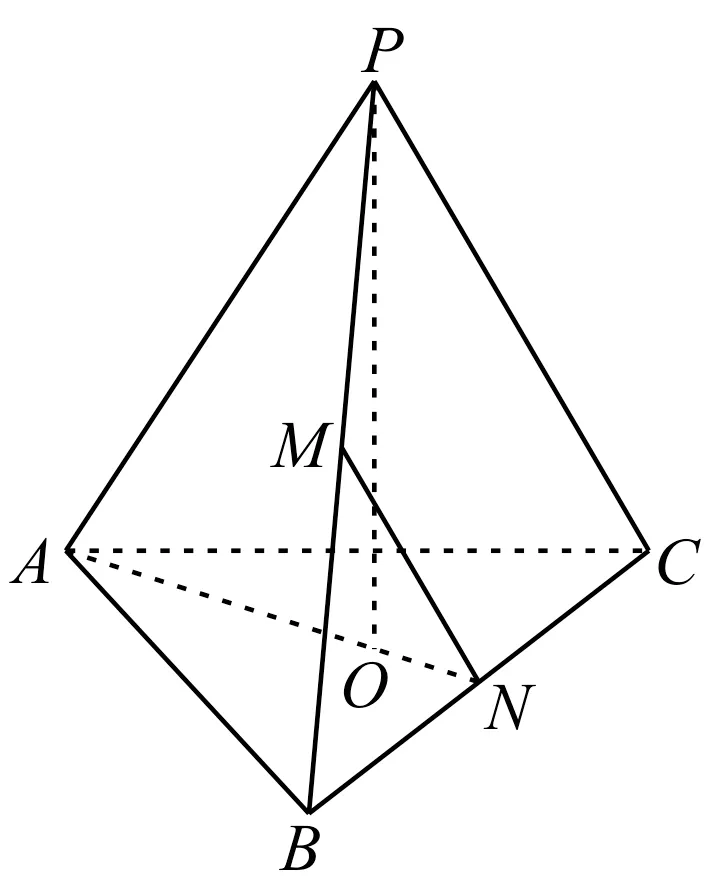
图2

(1)若PB的中点为M,BC的中点为N,求AC与MN夹 角 的余弦值。

(2)求正三棱锥P-ABC的体积。

解：(1)利用平移法寻找异面直线所成的角。因为M,N分别为PB,BC的中点,所以MN∥PC,则∠PCA为异面直线AC与MN所成的角。在等腰△PAC中,由PA=PC=2,AC= 3,易得cos∠PCA=即为AC与MN夹角的余弦值。

(2)在正三棱锥P-ABC中,过点P作底面的垂线,垂足为O,则O为底面正三角形的中心,连接AO并延长交BC于点N,则AN=1,由此可得PO=故正三棱柱P-ABC的体积VP-ABC=

回味：平移法是求异面直线所成角的常用方法,异面直线所成角的取值范围是

聚焦4：空间中的平行与垂直问题

例4(2019年高考北京卷)如图3所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为 菱 形,E为CD的中点。

图3

(1)求证:BD⊥平面PAC。

(2)若∠ABC=60°,求证:平面PAB⊥平面PAE。

(3)在棱PB上是否存在点F,使得CF∥平面PAE? 说明理由。

解：(1)利用线面垂直的判定定理证明。

因为PA⊥平面ABCD,所以PA⊥BD。因为底面ABCD为菱形,所以AC⊥BD。

因为PA∩AC=A,且PA,AC⊂平面PAC,所以BD⊥平面PAC。

(2)利用线面垂直,证明面面垂直。

由底面ABCD是菱形,且∠ABC=60°,可得△ACD为正三角形,所以AE⊥CD。又AB∥CD,所以AE⊥AB。

由PA⊥平面ABCD,PA⊂平面PAB,可得平面PAB⊥平面ABCD,其交线为AB,再由面面垂直的性质定理知AE⊥平面PAB。又因为AE⊂平面PAE,所以平面PAB⊥平面PAE。

(3)利用平行四边形的性质和线面平行的判定定理进行判断。

存在点F,当点F为PB中点时,满足CF∥平面PAE,其理由如下。

分别取PB,PA的中点为F,G,连接CF,FG,EG。在三角形PAB中,FG∥AB且。在菱形ABCD中,E为CD中点,所以CE∥AB且CE=AB,所以CE∥FG且CE=FG,即四边形CEGF为平行四边形,所以CF∥EG。

又CF⊄平面PAE,EG⊂平面PAE,所以CF∥平面PAE。

回味：证明面面关系的核心是证明线面关系,证明线面关系的核心是证明线线关系。要熟练掌握线线平行、线面平行、面面平行的证明方法以及线线垂直、线面垂直、面面垂直的证明方法。

1.已知l,m是平面α外的两条不同直线,现给出下列三个论断:①l⊥m;②m∥α;③l⊥α。

以其中两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:___。

提示：本题属于开放性问题,将所给论断,分别作为条件、结论,可得三个命题,利用线面位置关系推理判断即可。

(1)如果l⊥α,m∥α,则l⊥m。由线面平行和垂直的定义知,此命题正确。(2)如果l⊥α,l⊥m,则m∥α。有可能m在平面α内,此命题不正确。(3)如果l⊥m,m∥α,则l⊥α。有可能l与α斜交或l∥α,此命题不正确。

答案为:如果l⊥α,m∥α,则l⊥m。

2.如图4所示,在直三棱柱ABC-A1B1C1中,D,E分别是BC,AC的中点,AB=BC。

图4

求证:(1)A1B1∥平面DEC1。

(2)BE⊥C1E。

提示：(1)因为D,E分别为BC,AC的中点,所以ED∥AB。在直三棱柱ABC-A1B1C1中,AB∥A1B1,所以A1B1∥ED。因为ED⊂平面DEC1,A1B1⊄平面DEC1,所以A1B1∥平面DEC1。

(2)因为AB=BC,E为AC的中点,所以BE⊥AC。因为三棱柱ABC-A1B1C1是直棱柱,所以CC1⊥平面ABC。 又因为BE⊂平 面ABC,所 以CC1⊥BE。 因 为C1C⊂平面A1ACC1,AC⊂平面A1ACC1,C1C∩AC=C,所以BE⊥平面A1ACC1。又C1E⊂平面A1ACC1,所以BE⊥C1E。