基于深度神经网络的水声信号恢复方法研究∗

王全东 郭良浩 闫 超

(1中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

(2中国科学院大学 北京 100049)

0 引言

海洋环境下，水声目标信号常常被强干扰或背景噪声所掩盖，造成水声目标识别十分困难。因此，为提高识别的有效性和可靠性，抑制干扰因素，还原目标信号波形显得尤为重要。水声被动信号恢复技术旨在研究处理被动接收信号，适应海洋环境的复杂性，抑制干扰和背景噪声的同时保证目标信号不失真，从而恢复目标信号波形，对国家安全、海洋监测及开发等领域有重要意义。

在单阵元观测情况下，目前学者已提出了很多算法来解决信号降噪问题。谱减法最早被Boll[1]提出，是将噪声谱从接收信号谱中减去，但会引入不自然的人工噪声；基于最小均方误差的降噪算法包括Ephraim等[2]提出的最小均方误差估计器，以及Cohen等[3]提出的最优对数幅度谱估计法，这些方法能降低人工噪声，但是需要对噪声谱进行估计，在信噪比较低时难以取得满意效果；其他经典算法包括经验模态分解[4]、小波变换[5-6]、奇异谱分解[7]和单阵元盲源分离[8-9]，这些算法通常需要对噪声的能量大小、概率密度分布和统计特性做出较多的先验假设，然而在实际海洋条件下这些假设很难满足。

在多阵元观测情况下，算法可以同时利用空域和频域信息，因而可以取得较单阵元更显著的降噪效果[10]。过去几十年来，水声阵列信号降噪的研究工作主要集中在波束形成理论上。波束形成技术通过噪声干扰抵消达到阵列降噪的目的，是改善信噪比的有效手段。一般地，波束形成类方法分常规波束形成(Conventional beamforming,CBF)和自适应波束形成。常规波束形成可在保持信号幅度不变的同时，衰减干扰噪声信号。该类方法鲁棒性强，实现简单，但在干扰方位与目标方位临近的情况下难以抑制强干扰。自适应波束形成包括最小方差无失真响应波束形成(Minimum variance distortionless response,MVDR)、广义旁瓣消除器(Generalized sidelobe canceller,GSC)、最大信噪比波束形成器等。MVDR由Capon[11]最先提出，对期望信号进行无失真约束，同时使得总的输出功率最小。该类方法具有较好的方位分辨率和较强的干扰抑制能力，但其需要已知精确的期望信号方位，对参数失配非常敏感。Cox等[12]提出对白噪声增益进行约束，从而导出了对角加载MVDR，提高了对基阵误差的稳健性。对角加载MVDR因操作简单而广泛应用，Du等[13]针对加载量不易确定的问题提出了全自动对角加载算法，进一步提高了鲁棒性。Griffths等[14]引入了GSC作为MVDR的一种等价形式，GSC将固定波束形成器与自适应滤波器结合，显著降低了MVDR计算量。针对GSC的方位敏感问题，研究人员提出利用特征分析技术提取干扰噪声子空间，降低了阻塞矩阵的信号泄漏[15]。总的来说，自适应波束形成取得了显著进展，但其依然对目标信号方位和阵元位置有着较高的要求。在浅海垂直阵条件下，在多途作用下阵元之间的相关性较低，尽管距离较近时可采用聚焦波束形成来进行降噪和定位[16-17]，但远距离情况下依然较难准确获得目标信号在各阵元的到达时间差(Time difference of arrival,TDOA)，因而很难通过波束形成达到降噪的目的。

最近几年，深度学习理论在图像处理、语音识别、人工智能等重要领域取得了成功。深度神经网络(Deep neural network,DNN)作为一种卓越的信号处理模型，具有强大的建模能力，是由数据驱动的，因而能将已有的数据应用起来完成分类、回归等任务[18]。目前已有研究人员将浅层神经网络和深层神经网络用于水声定位研究中[19-21]，取得了显著进展。这种监督学习的方法也可以用于估计带噪信号和目标信号之间的复杂的非线性映射，具备更强的能力去从噪声中分辨目标信号，对比传统无监督方法已显示出了卓越的性能提升[22]。目前已有采用DNN进行主动声呐信号降噪的方法[23]，但是这种方法只适用于单阵元接收信号，也仅在仿真中对加性白噪声进行了抑制，对于其他真实情况下干扰或噪声的抑制还没有进行研究。

本文提出一种适用于水声被动目标信号波形恢复的方法，此方法能够自适应地学习目标信号自身的时频特征，有效去除不符合目标信号特征分布的噪声，在保真目标信号的同时，提高输出信噪比(Signal to noise ratio,SNR)。本方法不限定噪声的统计分布(各向同性噪声，临近方向干扰)，也对阵列排布没有限制，对训练数据集中不存在的信号具有一定的泛化能力，因而可以应用在各种阵列条件下。首先，在单阵元被动接收情况下，本方法采用DNN作为回归模型，估计带噪信号到纯净信号之间的映射函数，将时间上扩帧的带噪对数功率谱特征(Log-power spectra,LPS)映射为纯净的LPS，再结合带噪相位利用重叠相加法[24]将信号变换回时域。本文进一步采用DNN同时估计纯净LPS和理想比率掩蔽(Ideal ratio mask,IRM)以提高DNN输出的稳健性。第二，提出阵列DNN方法，将多个阵元的LPS特征拼接为一个长向量作为DNN的输入，从而利用阵列空间信息来恢复目标信号。同时研究了不同阵元规模情况下如何有效利用阵列信号中的时间信息和空域信息。第三，在阵列DNN的基础上提出了两阶段融合DNN模型，第一阶段将阵列分为若干个子阵，分别利用每个子阵训练阵列DNN，第二阶段将第一阶段降噪后的特征以及所有阵元的带噪特征一起输入一个DNN进行特征融合训练，这样的两阶段DNN处理可看作一个组合模型，第一阶段主要利用时间信息，第二阶段主要强调空间信息，因而能全面利用各阵元包含的丰富时频域信息。实验证明单阵元DNN能明显提高输出信号质量，抑制噪声，最后的两阶段DNN模型可以取得上述模型中最佳的处理效果。

本文内容安排如下：第一部分介绍神经网络回归理论和单阵元DNN模型。第二部分阐述提出的阵列DNN模型和两阶段融合模型。实验结果和分析为第三部分。最后一个部分为结论。

1 单阵元DNN模型

1.1 信号模型

考虑一个任意的M阵元的接收阵。阵列接收信号经过短时傅里叶变换(Short time Fourier transform,STFT)后在频域表示为M维向量Z(ωl,k)，

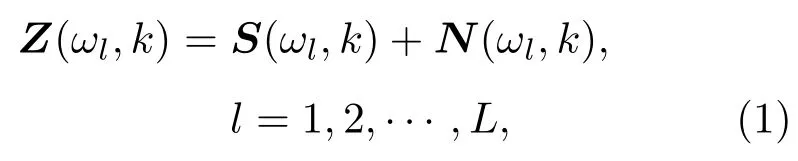
其中，Z(ωl,k)=[z1(ωl,k)zi(ωl,k)···zM(ωl,k)]T代表接收向量，S(ωl,k)=[s1(ωl,k)si(ωl,k)···sM(ωl,k)]T代 表M维 信号向 量，N(ωl,k)=[n1(ωl,k)ni(ωl,k)···nM(ωl,k)]T为M维 噪声或干扰向量，(·)T代表转置。zi(ωl,k)、si(ωl,k)和ni(ωl,k)分别代表第i阵元的接收信号、目标信号和噪声，i=1,···,M。ωl为离散频率，l为频率索引，L为处理的频率点数，k为时间帧索引。为简洁描述，文章余下部分省略ωl。当M=1时，接收信号简化为单阵元信号。

1.2 神经网络回归模型

在人工神经网络理论中，无限逼近定理[25-26]为DNN强大的映射学习能力提供了理论基础。无限逼近定理表明，一个仅有一个隐藏层的前馈多层感知机含有一个任意的连续S型函数和有限神经元数量，可以在Rn的子集上以任意精度逼近任意连续的函数。

令σ为任意连续S型函数，如sigmoid函数。In代表n维单位超立方体[0,1]n。In上的实值连续函数空间表示为C(In)。无限逼近定理表述如下[26]：函数形式

在C(In)中是稠密(dense)的， 其中N为整数，βj,θj∈R为实参数，yj是实向量。换言之，给定任意f∈C(In)和ε＞0，总有一个函数G(x)，对于所有x∈In满足|G(x)-f(x)|＜ε。

人工神经网络的函数逼近误差是有界的[25]。对于一个单隐藏层含有N个S型神经元节点的前馈网络，网络逼近函数的积分平方误差在cf/N内，cf取决于被逼近函数的傅里叶变换的模。分析公式(2)可知，最简单的回归网络结构含有一个输入层，对应于形式一个隐藏的S型函数层，对应于和一个线性输出层来对所有神经元的值进行加权求和作为最后的标量输出G(x)。最近，上述向量对标量的多层感知机映射已被拓展到高维的向量对向量的深度回归模型[22]，也即输出不再是一个标量而是一个多维向量，可以利用其映射能力来研究水声被动信号恢复问题。在本文中所用深度神经网络的结构如下：输入向量x由接收信号的L维LPS特征构成，LPS特征即为log(PZ)，其中PZ为功率谱，输出也为一个向量，其中包含恢复出的目标信号的LPS特征，中间不再只有一个隐藏层，隐藏层节点数为N。

1.3 单阵元DNN

在单阵元条件下，本文提出用DNN回归模型来进行水声目标信号恢复。如图1所示，其处理过程包括两个阶段：训练阶段和测试阶段。对于训练阶段，首先构造一个训练数据集，然后提取训练所需的特征，设计好DNN结构并进行训练。DNN的输入为接收信号的LPS进行扩帧后的特征，输出为纯净的目标信号的当前时间帧的LPS特征。DNN的目标函数E为输出的LPS特征ˆSk与纯净目标信号LPS特征¯Sk的均方误差(Mean square error,MSE)，表示如下：

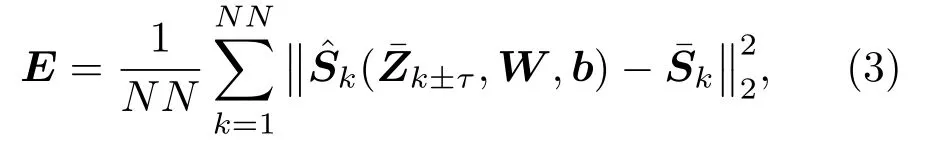
其中，NN为批处理个数，k和k的维数均为L，分别为输出的LPS和纯净的LPS，k±τ=[¯Zk-τ,k-τ+1,···,¯Zk,¯Zk+1,···,k+τ]为扩帧拼接的输入带噪LPS特征，扩帧窗长R=2τ+1，而(W,b)为DNN的权值和偏置的集合。扩帧能使DNN同时学习时间和频域尺度上的信息，有助于DNN分辨目标信号和噪声干扰。DNN可以用随机梯度下降法来最小化目标函数直至收敛完成训练。在此基础上本文采用多目标(multi-target)训练，将IRM特征作为正则项与纯净LPS一同作为输出以期进一步提高DNN的泛化能力[27]。L维IRM特征定义如下：

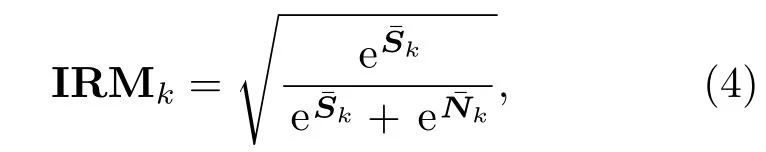
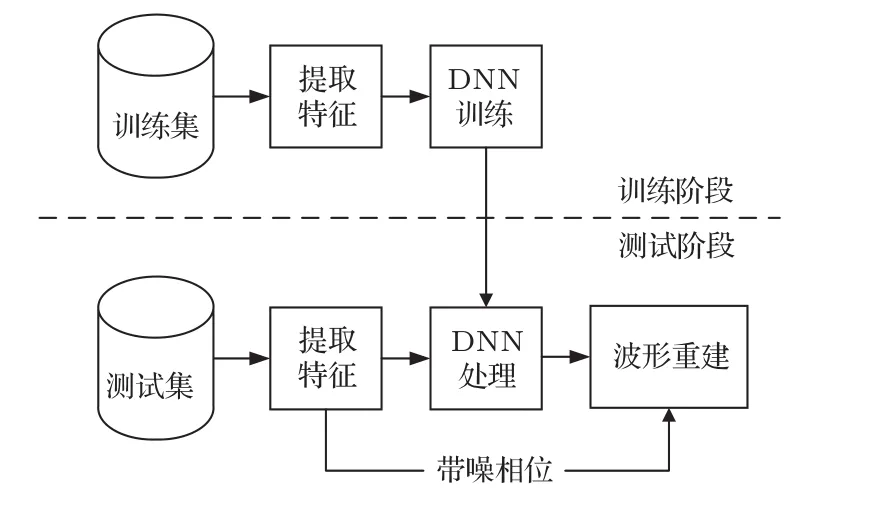
图1 单阵元DNN处理框图Fig.1 The block diagram of the single-sensor DNN method

加入IRM后的目标函数变为

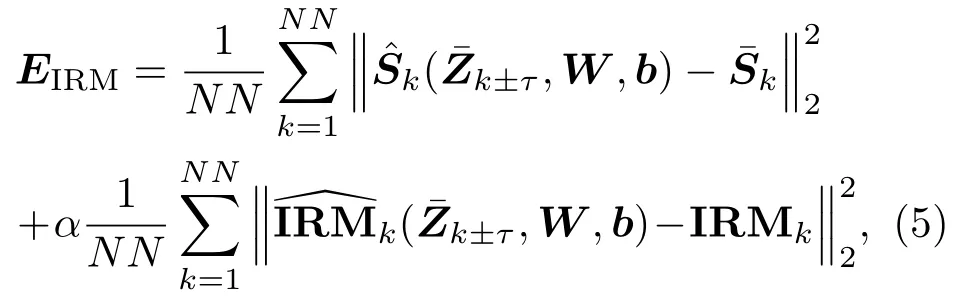
在测试阶段，分别提取需降噪的信号的LPS和相位，将带噪LPS输入DNN处理，输出恢复的LPS特征。有研究表明，带噪相位本身就是对纯净相位的一种最小均方误差估计[2]，因而可以将恢复的特征与带噪相位结合进行反短时傅里叶变换(Inverse short-time Fourier transform,ISTFT)，并用重叠相加法[24]恢复为时域波形。

2 基于阵列的DNN模型

2.1 阵列DNN

针对阵列接收信号降噪问题，本文提出阵列DNN算法，将多个阵元的带噪特征拼接在一起形成一个长向量作为DNN输入。在受限的DNN宽度(隐层单元数)下，若将K(K≤M)个阵元信号分别扩帧后再拼接，输入维数将达到L×R×K，可能会造成输入维数过高，难以完成稳定的训练或造成过拟合。因此，本文控制了时间窗长的大小使得输入维数在不同阵元数条件下可比，并研究了不同阵元数的降噪性能。可将任一阵元设置为参考阵元，从阵列带噪信号中估计参考阵元中的目标信号波形。利用多目标训练，阵列DNN的目标函数表示为

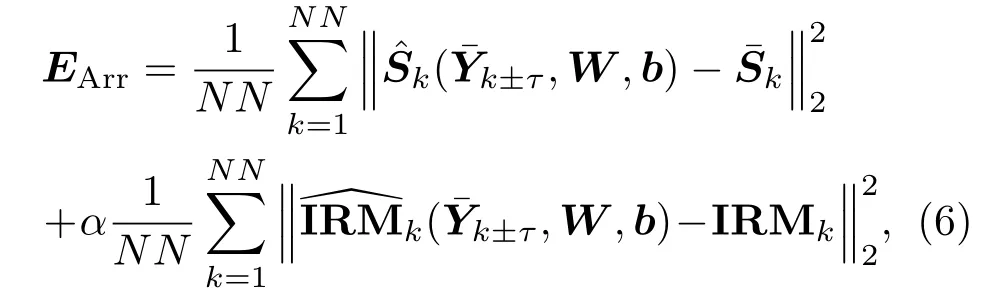
其中，当K＜M时，=[¯Z1,k±τ,···,¯ZK,k±τ]为K个阵元各自扩帧后的拼接输入向量，¯Zi,k±τ为扩帧的第i个阵元的带噪LPS，当K=M时，τ=0各阵元不进行扩帧操作。这里的IRM目标由参考阵元的信号和噪声计算而来。由于不同阵元接收的是来自不同水声传播路径混合的信号，所以它们具有相关且互补的特征，因此可以让DNN学习到阵列中的空域信息。这种将多个阵元信号同时送入DNN并以最小均方误差作为损失函数的处理方式与波束形成类似，但不同点在于阵列DNN能够自适应学习非线性的映射函数。

2.2 两阶段融合DNN

如上文所述，阵元数较多情况下，阵列DNN仅将一部分阵元信号进行拼接作为输入时可以进行扩帧利用时间信息，但不能利用所有阵元的空间信息，而当阵列DNN拼接所有阵元的信号作为输入时，为控制输入特征总维数，将不会采取扩帧的操作而直接将所有阵元的当前时间帧拼接在一起，但这样不能充分利用时间信息，所以总体上由于输入维数限制，阵列DNN不能同时充分利用时间和空间上的信息。为解决这一问题，本文提出一种两阶段阵列DNN融合的处理方法。这是一个组合模型，其结构如图2所示。第一阶段是增强阶段，将M个阵元分为Q组，每一组K个阵元组成一个子阵，扩帧后采用阵列DNN进行训练，记为增强DNN。这里DNN不进行IRM的训练，以便输出给下一个阶段。这一阶段的每个DNN强调利用时间信息，但没有利用所有的阵元信息。第二阶段为融合阶段，在第一阶段的Q个DNN之上进一步挖掘阵列的空间信息，记为融合DNN。将增强阶段的Q个增强DNN输出和所有阵元带噪LPS特征拼接在一起作为融合DNN的输入去映射目标信号的LPS和IRM。融合DNN的目标函数定义为

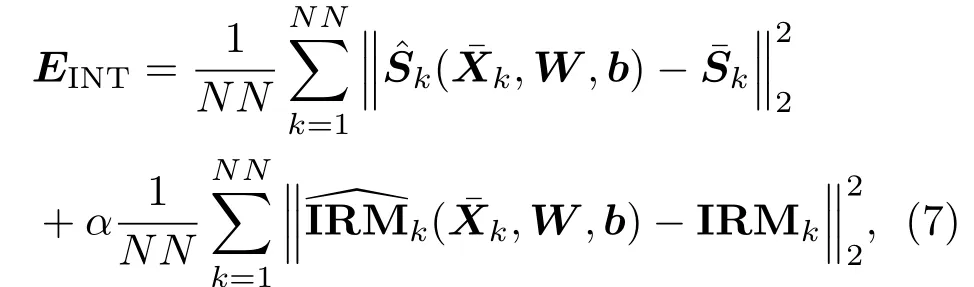
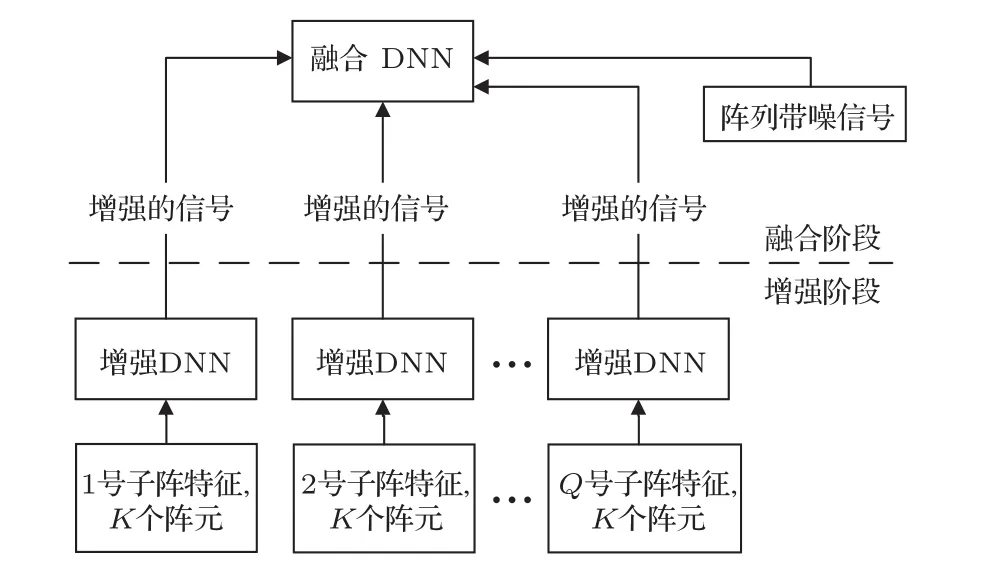
图2 两阶段融合DNN结构图Fig.2 The structure of the two-stage integration DNN

3 实验结果和分析

为验证本文所提方法的降噪能力，本文进行了七组对比实验。本实验采用一次海试实验中的船辐射噪声作为目标信号，其实验条件如下：声源深度为5 m，水深152 m，八阵元接收垂直阵深度为128～135 m，阵元间隔1 m；沉积层厚24 m，声速1572～1593 m/s，密度1.76 g/cm3；水底为流体半空间，声速5200 m/s，密度1.8 g/cm3；深度剖面为典型负梯度。本文选用时间段为2009年1月31日01:43-02:05，期间目标匀速逐渐远离接收阵。本文将公开数据集SWellEX-96[29]S5实验中的信号作为要去除的噪声，选取垂直阵前八个阵元的信号，所用时间段为1996年5月10日23:15-23:58，其有两个噪声源，较深的源发射信号为65个单频信号和FM chirp信号，较浅的源发射另外9个单频信号，所有单频信号在49～400 Hz之间。依据公式(1)合成阵列接收信号，单阵元接收SNR分别为-10 dB、-5 dB、0 dB、5 dB、10 dB。训练信号是将船辐射噪声数据的前17 min和SWellEX-96数据的前38 min拆分成多个时间片段，进行随机组合按信噪比混合在一起，得到一个约90 h记录时间的训练集。测试集信号为船辐射噪声最后6 min数据和SWellEX-96最后6 min数据混合而成，因而是训练数据集中不存在的，其信噪比设置与训练集相同。训练数据中的目标信号和噪声的时频图分别为图3和图4，可以看出目标信号与噪声的频域分布不同，目标信号和噪声都既包含连续谱也包含强线谱。

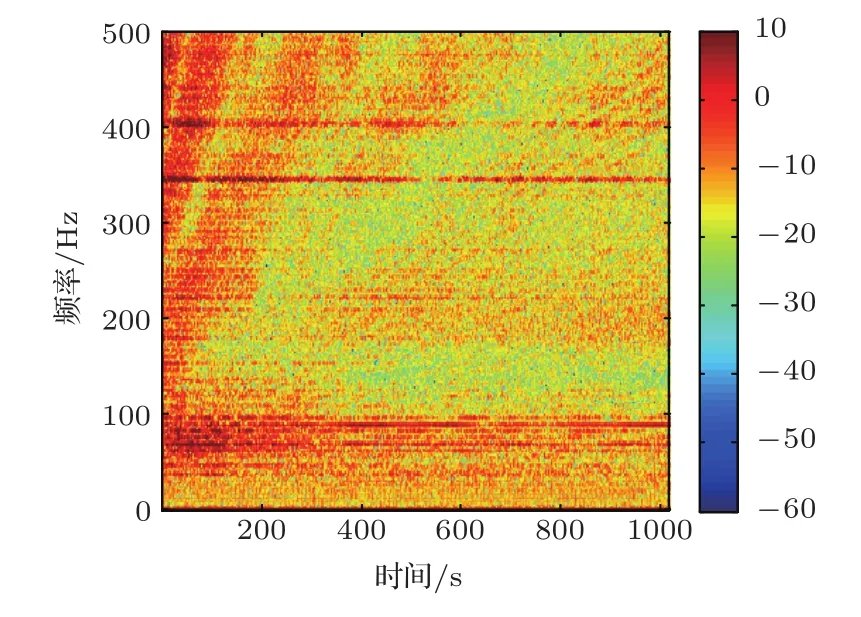
图3 前17 min目标信号时频谱Fig.3 The time-frequency spectrum(TFS)of the first 17 minutes of target signal

本实验的分析频带为0～500 Hz，频域分辨率为1.95 Hz，LPS特征维数为257(一帧)，IRM维数也为257维。降噪所用的DNN结构为输入层为线性层，中间为两层隐藏层，每层2048节点数，S型函数为sigmoid，输出层也为线性层。DNN初始学习率为0.00002，采用随机梯度下降法训练，批处理数量为32。训练IRM时，α为0.05。为检验算法降噪和保真的效果，采用两种客观描述参数。

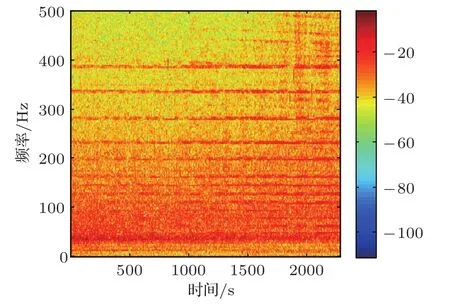
图4 前38 min噪声时频谱Fig.4 The TFS of the first 38 min of noise

第一个参数为输出SNR，定义为

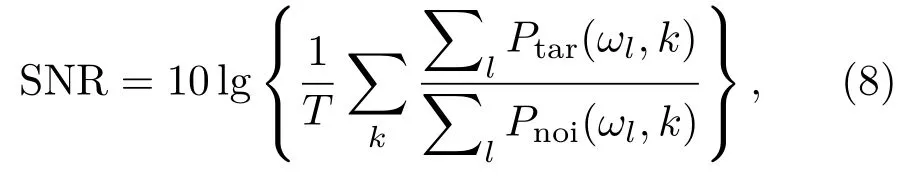
其中，T为输出时间帧总数，Ptar(ωl,k)和Pnoi(ωl,k)分别代表输出信号中目标信号的功率谱和输出信号中噪声的功率谱。需要指出的是，由于DNN为非线性处理，不能通过分别输入纯目标信号特征和纯噪声特征分别得到输出的目标信号特征和残余噪声特征来直接计算输出SNR，所以这里目标信号和噪声功率的估计方法如下：首先根据IRM确定带噪信号时频图上噪声占主导的时频区域，IRM值小于0.2处视为噪声区域，计算输出信号中这一区域的功率作为噪声功率，其他区域的功率作为目标信号功率。

第二个参数为输出功率的均方误差MSE，物理意义为输出信号的功率估计误差，定义为

其中，Ptest(ωl,k)和Pclean(ωl,k)分别代表待测试的输出信号的功率谱和纯净目标信号的功率谱。输出SNR和MSE是一组互补的参数，比如输出SNR增高的时候，MSE不一定减小，即输出能量未必跟原来相同。因此不同算法对比时，以下三种情况都可以认为达到了更好的恢复效果：SNR增大，同时MSE减小；MSE相当的情况下，SNR增大；以及SNR相当的情况下，MSE显著减小。

3.1 常规波束形成

本实验将第四个阵元(ch4)作为参考阵元，并在所有对比算法中估计第四个阵元中的目标信号。作为对比，采用水声环境下常用的CBF对阵列数据进行处理。常规波束形成算法流程简述如下：首先根据阵列位置和俯仰角扫描范围(0°～180°)确定阵列流形向量，然后利用较高频段的接收数据(300～500 Hz)来进行波束扫描，从而获得每一帧信号的扫描方位谱(接收协方差矩阵利用21个快拍来进行估计)，根据方位谱峰值所在的位置确定每一帧接收信号的俯仰角，并据此进行常规波束形成获得输出波形和功率谱。本文的俯仰角的零度定义为垂直向上方向。

作为测试示例，0 dB带噪测试信号的对数功率谱如图5所示，其中的噪声成分的对数功率谱为图6，真实目标信号的对数功率谱为图7。观察到噪声信号几乎将目标信号掩盖。下面给出CBF处理结果。图8展示了0 dB条件下CBF波束扫描后的入射俯仰角估计结果，图9为10 dB条件下的扫描结果。对比这两图可知，在较低信噪比和浅水多途条件下，较难获得准确的俯仰角估计结果。图10为0 dB下根据图8的俯仰角估计结果，利用CBF获得的输出信号的对数功率谱，可以看到噪声的强线谱依然清晰可见，没有得到很有效的去除，且由于入射俯仰角估计错误一些时间段的谱出现了异常。表1为各算法输出结果的两项客观描述参数在-10 dB～10 dB的平均结果。对比表1的第二行的第四号阵元的接收信号(记为ch4 mix)和第三行CBF输出结果，CBF算法能够一定程度上提高输出SNR，但是在多途作用下各阵元接收到的目标信号是不同的，因而CBF仅是将目标信号成分在不同阵元间进行了平均，难以取得理想平面波假设下的阵增益，导致CBF结果与参考阵元接收的目标信号相关性较差，所以导致了MSE参数反而上升了。

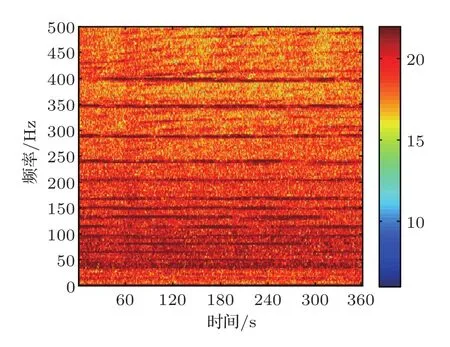
图5 0 dB测试带噪信号对数功率谱(ch4)Fig.5 The LPS of the testing signal at 0 dB(ch4)

图6 0 dB测试信号中的噪声的对数功率谱(ch4)Fig.6 The LPS of the noise in the testing signal at 0 dB(ch4)

图7 0 dB测试信号中的真实目标信号的对数功率谱(ch4)Fig.7 The LPS of the target signal in the testing signal at 0 dB(ch4)

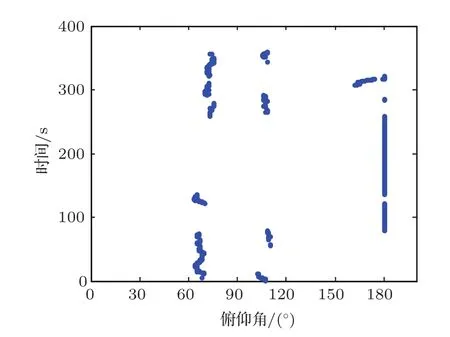
图8 0 dB下目标信号入射俯仰角扫描结果Fig.8 The pitch angle scanning(PAS)result of the target signal at 0 dB

3.2 单阵元DNN

下面利用DNN来进行目标信号恢复。单阵元DNN利用了第四阵元信号的时间信息和频域信息，其输入为扩帧LPS，维数为257×11×1，输出为当前帧257维LPS，记为‘ch4 noIRM’。如图11所示，将带噪信号输入单阵元DNN后输出的对数功率谱很接近图7，这显示出DNN具有强大的建模能力，显著抑制了噪声成分，目标信号恢复效果明显。对比表1的第三行和第四行，单阵元DNN输出SNR比CBF高5 dB以上的同时，显著降低了功率估计的MSE，表明本处理方法对测试信号有较强的泛化能力。

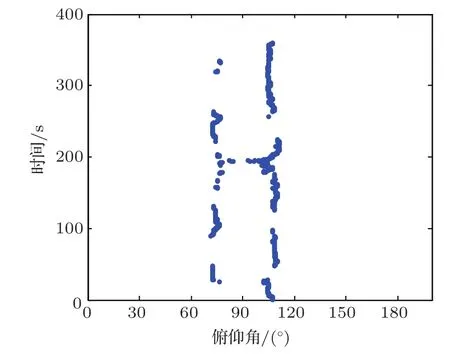
图9 10 dB下目标信号入射俯仰角扫描结果Fig.9 The PAS result of the target signal at 10 dB

图10 0 dB下的CBF输出的对数功率谱Fig.10 The LPS output by the CBF at 0 dB

表1 各个对比算法的输出参数在-10 dB～10 dB的平均结果Table1 The average objective measurements for all algorithms at-10 dB～10 dB

图11 0 dB下单阵元DNN输出的对数功率谱Fig.11 The LPS output by the single-sensor DNN at 0 dB

3.3 阵列DNN

根据第2.1的分析，由于DNN输入维数的限制，在利用较多阵元数时，需要降低扩帧的窗长来保证DNN训练的稳定。因此本实验研究了利用两个阵元(阵元4和阵元5，记为‘ch45’)、四个阵元(阵元3～阵元6，记为‘ch3456’)和八个阵元(阵元1～阵元8，记为‘8ch’)的情况，分别采用窗长R等于5、3、1，均没有训练IRM特征，标记为‘noIRM’。三者的输出结果列于表1的第六、第七、第八行，可以看出三个阵列DNN的恢复效果均优于单阵元DNN，表明使用阵元DNN利用了阵列的空间信息，提高了DNN估计的准确度。四阵元系统‘ch3456’的输出SNR与两阵元系统和八阵元系统相当，但是取得了三者之中最小的MSE，更好地估计了目标波形的功率大小。这说明在阵列DNN的框架下，阵元数越多不一定越好，综合利用空间信息和时间信息才能取得更佳的恢复效果。

3.4 单目标训练对比多目标训练

在DNN输出层不仅可以输出目标信号LPS，也可以估计IRM，即输出总维数为514。表1的第五行和第九行为单阵元DNN和八阵元DNN同时训练LPS和IRM的结果，标记为‘IRM’。在同等情况下，标记‘IRM’的系统在保持输出SNR相当时输出MSE的要明显优于标记‘noIRM’的DNN系统，说明多目标映射时，IRM作为目标函数中的正则项，与LPS一起训练，能提升DNN估计LPS的鲁棒性，更好地恢复目标信号功率。下面简述一下IRM正则项提高性能的原因。类似于文献[12]中在目标函数中加入正则项来提高MVDR的鲁棒性，本文式(5)、式(6)、式(7)加入右边第二项的正则化项后使网络进行多目标或多任务学习，由于IRM特征的物理意义为归一化的输入信噪比，所以相当于在估计LPS特征这个主要任务上多加了一个估计输入信噪比的附加任务。在机器学习理论中，通常来讲，用共享的神经网络来同时学习一个或多个额外的适当任务可以同时提高全部任务的学习能力，而在实际使用网络时可以将用于学习额外任务的参数去除。总的来说，IRM特征估计作为正则项可以限制深度神经网络参数，引入损失函数的归纳偏差，迫使学习算法在两个任务的交叉表征区域找到最终解，避免单任务下在一个更大表征区域求得局部最优解，因而可以降低网络过拟合风险使得网络更好、更快地收敛。

3.5 两阶段融合DNN

根据第3.3节的分析，为了全面利用八个阵元信号的时间和空间信息，本文训练了两阶段融合系统。第一阶段训练了两个增强DNN，分别为‘ch3456’和‘ch1234’(由阵元1～阵元4训练)。‘ch1234’与‘ch3456’性能接近，因此未列入表1。第二阶段中，将第一阶段的两个DNN的LPS输出和所有八个阵元的带噪信号拼接在一起，形成一个维数为257×10的向量作为输入，输出为LPS和IRM特征，共514维。图12为两阶段DNN处理0 dB测试信号后的对数功率谱，可以看到图7中目标信号在50～100 Hz之间、360 Hz和420 Hz处的线谱在图12中得到了很好的突出和保留，目标信号在180～240 Hz之间的连续谱也得到了有效恢复，说明本方法对目标信号和噪声的频域特性没有限制，因而适用性较好。两阶段DNN的平均输出参数结果如表1的最后一行所示，记为‘2stage’。特征融合后，其MSE略好于‘ch3456’，但输出SNR优于‘ch3456’1 dB以上。这说明，本方法能在两个四阵元阵列DNN基础上，进一步综合利用八个阵元的时间空间信息，取得了所有单阵元和阵列对比算法中最佳的信号恢复效果。其原因为，在融合阶段DNN的映射能力被再次利用，由于每个阵元的带噪信号中含有一部分较高信噪比的时频点，将其与降噪后的特征一同送入DNN本质上提高了训练的丰富度，因此融合DNN能从中学习并将第一阶段没有处理好的时频点进一步恢复。

图12 0 dB下两阶段融合DNN输出的对数功率谱Fig.12 The LPS output by the two-stage DNN at 0 dB

3.6 DNN的恢复性能随输入信噪比变化情况

为着重讨论DNN目标信号恢复算法在不同输入SNR条件下的性能变化，在图13和图14中对比了CBF、单阵元DNN和两阶段DNN的两种描述参数。由于CBF的MSE远高于本文的DNN算法，故均方误差由对数MSE，即10log(MSE)来衡量。三种算法的输出SNR随输入SNR增大而增大，对数MSE随输入SNR增大而减小。然而CBF的对数MSE始终高出DNN输出结果30以上，说明CBF的功率估计远不及DNN准确。随着输入SNR增大，两阶段DNN的输出SNR与CBF的输出SNR的差距从10 dB减小到了2 dB，DNN方法比CBF在低SNR下有着更加突出的优势。此外，两阶段DNN在低SNR条件下比高SNR条件下展示出相对单阵元DNN更加明显的优势，这表明两阶段DNN算法融合阵列的丰富时域空域信息对于低SNR接收信号有着更重要的意义。

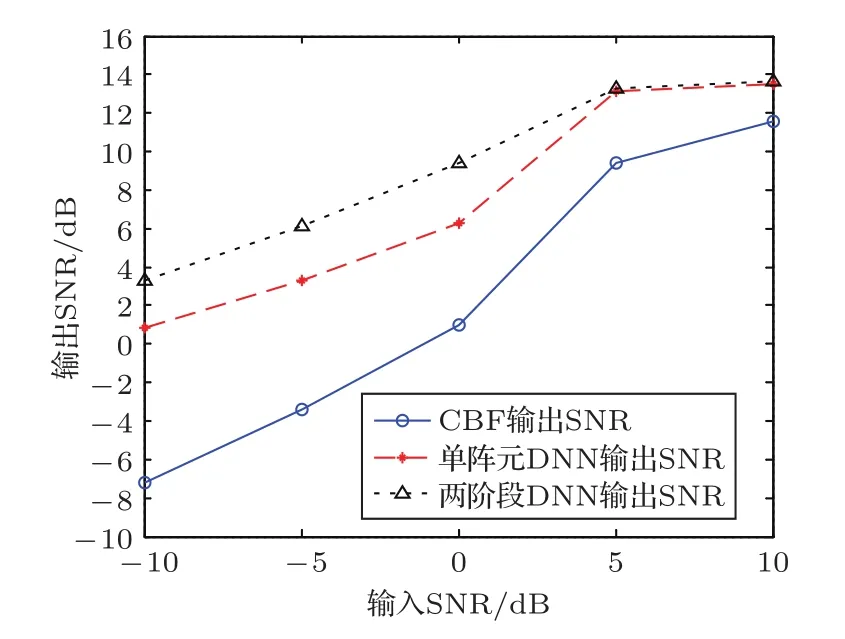
图13 不同输入SNR下三种算法的输出SNR对比Fig.13 Output SNR comparisons between three methods under different SNRs

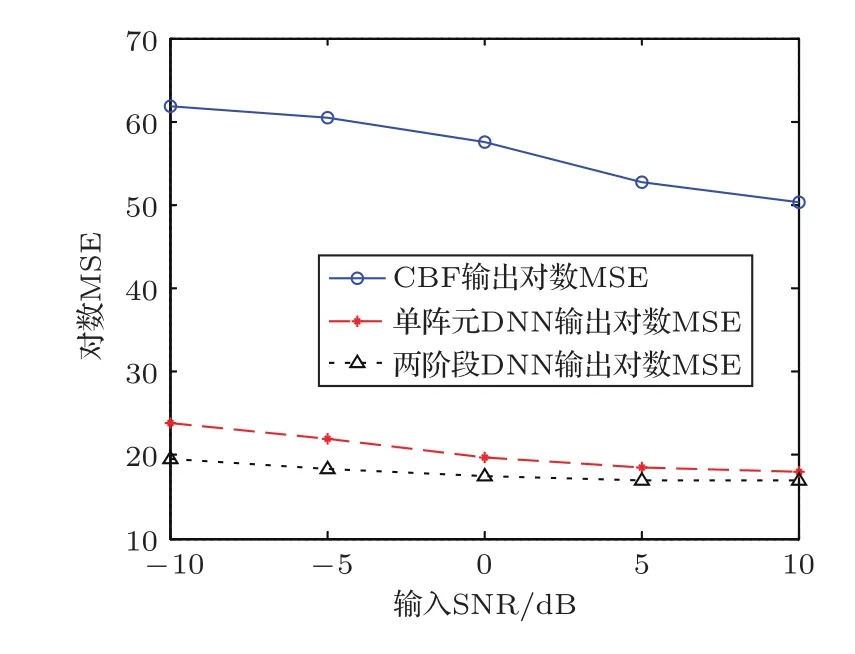
图14 不同输入SNR下三种算法的对数MSE对比Fig.14 Log-MSE comparisons between three methods under different SNRs

3.7 DNN的恢复性能随频率变化情况

为体现本文方法能够自适应学习目标信号的时频特征，计算了以频率为变量的输出SNR，其定义如下：

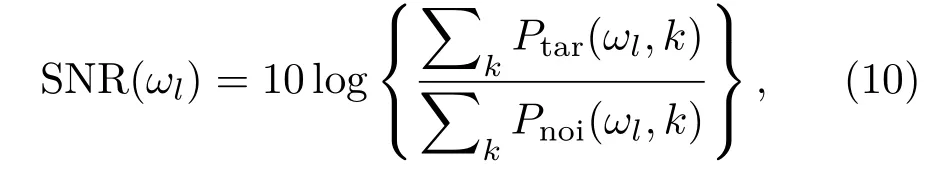
因为DNN只输出单路LPS， 所以Ptar(ωl,k)和Pnoi(ωl,k)两者难以分开，故采用真实目标信号 的 功 率 谱Pclean(ωl,k)来 近 似Ptar(ωl,k)， 用Ptest(ωl,k)-Pclean(ωl,k)来近似Pnoi(ωl,k)，从而近似估计单频SNR。

图15对比了在0 dB测试条件下的CBF、单阵元DNN和两阶段DNN在全部频点上输出的SNR。从图中可以看到，带噪信号的SNR在噪声频点处(如200 Hz左右、350 Hz左右和400 Hz左右等)有非常明显的谷点，也即这些频率的信号质量非常差。经过CBF，这些频点的SNR有所增加，然而还是有明显的谷点。经过本文DNN处理后，这些噪声谷点被基本消除，其中两阶段DNN在各个频点的输出SNR最高。此外，可以看到DNN输出的SNR在原目标信号的功率较强的频率点上出现了峰值(如100 Hz左右和360 Hz左右)，较好地恢复了目标信号原有的频率分布。

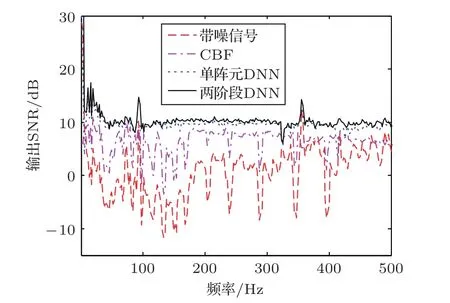
图15 0 dB条件下全部频点处CBF、单阵元DNN和两阶段DNN的输出SNR对比Fig.15 The output SNR comparisons between CBF,single-sensor DNN and two-stage DNN at different frequencies at 0 dB

为体现DNN在不同频率下的恢复性能差异，在图15基础上计算了全部频率下三种算法的SNR增益，如图16所示。可以看到，三种算法在噪声强线谱频点上均有较大的SNR增益的峰值，其中两阶段DNN的SNR增益最高。结合图15可以得到以下结论，DNN恢复算法在噪声较强的频点上具有更高的SNR增益，所以能抑制噪声并准确恢复目标信号的频率分布。对比图7、图10和图12中真实目标信号的对数功率谱、CBF和两阶段DNN的处理结果，可以看出两阶段DNN输出信号比CBF输出信号更接近真实目标信号。由此说明本文DNN处理方法能够自适应地学习目标信号自身的时频特征，有效去除不符合目标信号特征分布的噪声。

图16 0 dB条件下全部频点处CBF、单阵元DNN和两阶段DNN的输出SNR增益对比Fig.16 The output SNR gain comparisons between CBF,single-sensor DNN and two-stage DNN at different frequencies at 0 dB

4 结论

本文提出了一种基于DNN的水声目标信号被动恢复方法。DNN作为回归模型，具有强大的建模能力，建立了带噪对数功率谱特征到纯净对数功率谱特征的多维映射函数。本方法在单阵元下利用时间和频谱信息恢复了目标信号，并利用多目标训练提高了鲁棒性；在接收阵情况下采用阵元DNN同时将阵列信号映射到参考阵元，提高了空域信息利用能力，并探讨了时间窗和阵元数的限制关系；在此基础上提出两阶段处理算法来融合降噪后的特征和所有空域带噪特征，进一步提高了目标信号恢复能力。实验数据处理结果表明，本方法能显著去除噪声，输出比常规波束形成更高的SNR并准确估计目标信号能量。本方法优势在于能够从大量训练数据中学习目标信号的先验信息，将其有效应用于测试信号，对于训练集中不存在的信号有一定的泛化能力，且本方法对噪声分布和阵列排布没有要求，能够有效恢复线谱和连续谱信号。本文实验的训练数据和测试数据有一定相关性，但在实际应用中，目标信号可能会叠加不同种类的噪声或干扰，因此如何提高在其他恶劣条件下的目标波形恢复的稳健性需要进一步研究。此外，由于本文的实验为垂直阵数据，阵元之间的相关性较差，因此DNN在利用更多阵元数时，没有体现出类似于波束形成在平面波条件下的增益变化，下一步将研究提高阵元相关性来进一步提高阵列DNN处理的增益。