基于ARX系统辨识模型的钢绞线张拉力识别∗
2019-12-04李长春罗映相张俊波
钱 骥 李长春 罗映相 张俊波
(1重庆交通大学土木工程学院 重庆 400074)
(2重庆交通大学 山区桥梁结构与材料教育部工程研究中心 重庆 400074)
0 引言
预应力钢绞线广泛应用于土木工程建筑物,更是大跨度桥梁最重要的受力构件,如梁桥的预应力主筋、拱桥吊杆及斜拉桥拉索等。钢绞线长期处于高应力状态,对环境侵蚀及结构徐变非常敏感,经常出现实际保有应力值下降的现象,从而衍生结构开裂、下挠等病害,降低大跨度结构的承载能力和耐久性。通常,钢绞线由于其防腐蚀需要而处于层层保护之中,在其防腐性能提高的同时也增大了钢绞线日常检测、监测的难度。在役结构钢绞线应力检测评估一直是土木工程领域面临的技术难题,相对成熟的钢绞线应力测试技术聚焦于应力增量的检测且需在早期预埋,无法满足大量在役预应力及索结构的应用需求。
超声导波是近年来研究较多的一种结构无损检测方法,相比于传统超声波检测使用的体波,导波由波导介质边界多次反射形成,其传播特性与介质的边界条件及局部缺陷密切相关,能够反映波导体的缺陷特征及力学边界变化,目前已应用于管道、锚杆等结构的缺陷检测[1-2]。相比与管道、锚杆这类规则构件,超声导波在钢绞线中的传播特性更为复杂。Kwun等[3]、Treyssède等[4]、Bartoli等[5]通过实验及半解析有限元等方法提出了钢绞线张拉力引起的导波模态缺失现象。Rizzo等[6-7]、Chaki等[8]、Nucera等[9]、Liu等[10]、吴斌等[11]研究了导波时频域特征参数随钢绞线张拉力变化规律,构建了钢绞线张拉力识别因子,但受应力状态、传播距离影响较大,直接以导波波速的变化判别钢绞线应力值敏感度偏低。刘增华等[12]通过波动理论、声弹性理论和实验相结合的方法,得出应力在0.5 GPa以上时,钢绞线中L(0,1)模态的群速度会随着应力增大呈近似线性下降,实验结果与理论结果吻合较好。钱骥等[13-14]通过实验及有限元模拟等方法提出了导波能量熵谱和模态转角的方法,建立了导波模态转角和钢绞线张拉力之间的幂函数关系。众多研究成果表明,钢绞线中导波传播携带有明显的张拉力信息,但提出具有宽泛实用条件的张拉力识别方法仍需要进一步的研究。
本文以工程结构中常用的7芯钢绞线作为研究对象,通过进行不同应力条件下钢绞线导波传播实验,将钢绞线中导波传播过程假定为独立系统,通过辨识系统模型参数随钢绞线应力变化规律,构建具有更高敏感性的张拉力识别指标,最后讨论了传感器布置位置、钢绞线加卸载等因素的影响。
1 ARX系统辨识模型
弹性波在固体中的传播是一个弹性动力学问题,通过波动方程并代入几何边界条件和力学边界条件,可求解模态特征方程。对于单根高强钢丝而言,经典柱波导理论已可求得纵波、弯曲波、扭转波等模态曲线。但是,钢绞线结构复杂,多根钢丝接触耦合问题使得建立导波传播数学模型非常困难,目前尚无解析解。
钢绞线在使用过程中,各种外界因素引起的实际保有应力值变化都将直接引起内部钢丝间接触力发生变化,该力学边界条件的改变会引起其间传播的导波模态发生变化。在难以直接解析钢绞线导波模态随张拉力变化规律时,可考虑将导波传播过程理解为一个独立系统,通过外在的导波输入和输出来辨识该系统的模型参数,从而建立模型参数随钢绞线张拉力变化规律。
系统辨识的目的是根据系统的输入、输出,利用某种误差准则来确定描述系统行为的数学模型[15]。ARX模型由于不需要知道过程内部复杂的物理机理,因此被视为一种“黑箱”模型,模型的建立过程一般包括以下三个基本步骤:
(1)输入、输出数据的采集与预处理;
(2)模型结构的选择和参数估计;
(3)模型的验证。
ARX模型结构简单、鲁棒性强,在噪声较小时,辨识精度高;在噪声较大时,可适当提高模型的阶次,来补偿噪声对辨识精度的影响。ARX模型表示形式如下[16]:
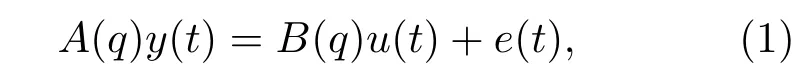
式(1)中:u(t)为输入序列;y(t)为输出序列;e(t)为零均值的随机噪声;A(q)、B(q)为关于平移算子q的多项式,定义为

将式(1)展开为输出形式:
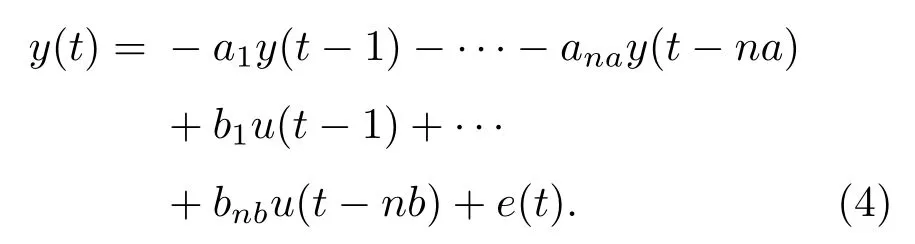
式(4)可表示为

式(5)中:φ为样本集合;θ为被辨识的参数的集合,θ=[a1,a2,···,ana,b1,b2,···bnb]。进而可以将式(5)写成向量形式:

取残差的平方和为准则函数[16]:

求出θ的最小二乘估计值θLS的必要条件为

将式(7)代入式(8)中,可以得到

如果式(9)中ψTψ满秩,则[ψTψ]-1存在,从而可以得出

根据最小二乘辨识过程,未知模型参数θ最可能的值是在实际观测值与计算值之间累计误差的平方和达到最小值时,这种估计模型的输出能够更好地接近实际过程的输出。
2 定义钢绞线张拉力识别指标
基于ARX模型参数来识别钢绞线张拉力大小的过程是通过提取各个不同张拉力条件下系统模型的自回归参数作为特征向量,以钢绞线张拉到70%Fm(Fm为钢绞线最大力)状态下的模型参数作为基准值,计算各张拉力状态下模型参数与基准值之间距离作为张拉力识别指标Istf。假设70%Fm张拉力状态下的系统ARX模型为
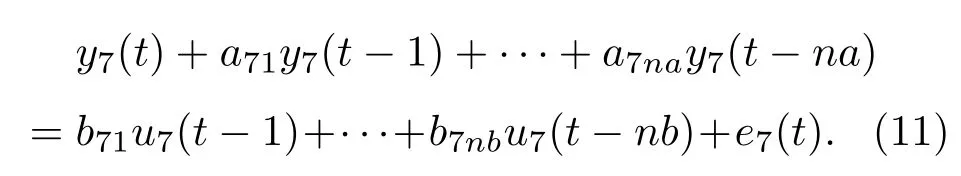
取模型参数a71,a72,a73,···,a7na构成特征向量作为指标值Istf计算的基准值,(20%~60%)Fm张拉力状态下的模型为
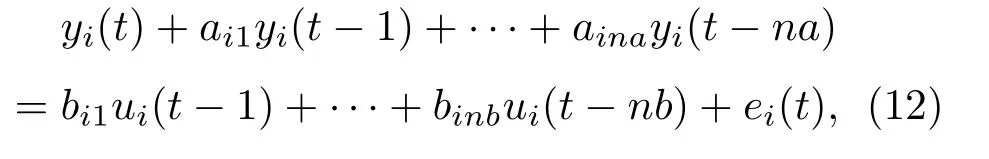
式(12)中,i取2、3、4、5、6。以参数ai1,ai2,ai3,···,ain构成特征向量作为指标值Istf计算的状态值,计算Istf如下:
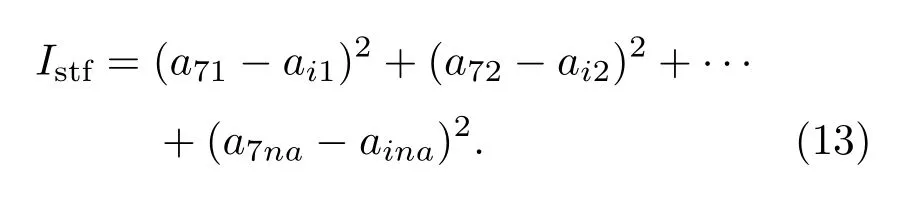
识别指标Istf反映了由张拉力引起的钢绞线导波传播特征的变化。
3 实验
采用钢绞线张拉锚固综合试验台进行逐级加卸载实验(图1~2)。钢绞线为工程中常用的公称直径D=15.2 mm七芯钢绞线,总长度L=5.5 m,几何参数及材料参数如表1所示。钢绞线一端锚固,一端张拉,最大张拉力为182 kN(70%Fm)。先将钢绞线张拉至52 kN(20%Fm),接下来每次依26 kN(10%Fm)进行逐级加卸载,直至加载到70%Fm。
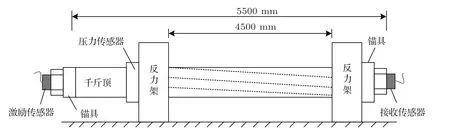
图1 实验布置Fig.1 Layout of experiment

图2 钢绞线张拉锚固试验系统Fig.2 Equipment for strands tensioning and anchoring
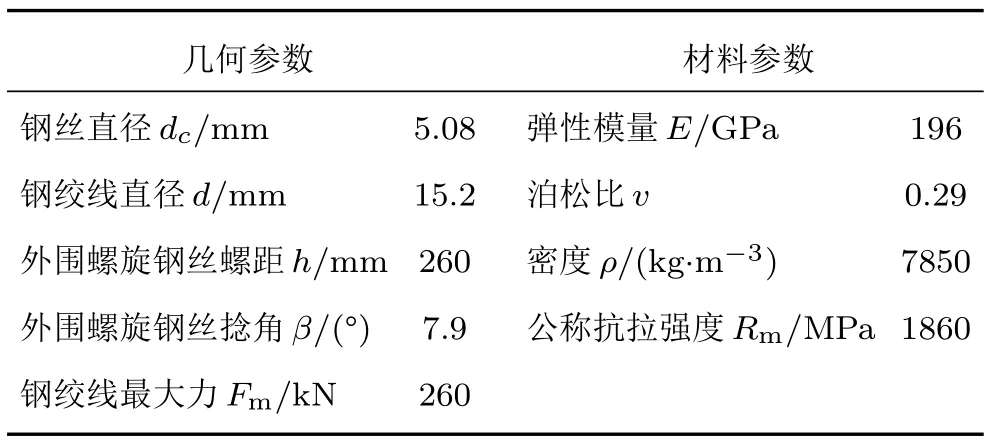
表1 钢绞线几何及材料参数Table1 Geometry and material parameters of steel strand
导波激励与采集系统为美国PAC生产的PCI-2声发射监测系统,系统可识别频率范围0~4000 kHz,传感器采用WD宽频压电换能器,频带范围100 kHz~1000 kHz,信号采样率2000 kHz。导波激励为步径频率Δf=50 kHz的一系列单周期正弦脉冲,激励波源函数如式(14)所示:

其中:Vi为矩形窗函数,f0=100 kHz为起始频率,f=1000 kHz为截止频率,Δf=50 kHz为步径频率,矩形窗的窗长Ti=1/f0+i·Δf。

图3 接收传感器的布置Fig.3 Layout of receiving sensors
导波激发和接收传感器(系统输入和输出)布置在钢绞线两端(图3)。实验过程中,传感器保持接触状态不变,当钢绞线加卸载至预定荷载且持载2 min后,激发端产生激发脉冲,接收端过门槛自动采集。
4 实验结果分析
4.1 钢绞线ARX模型的建立
激发端输入波形(输入波形是通过公式(14)得出的一系列100 kHz~1000 kHz的单周期正弦脉冲信号)如图4(a)所示,不同张拉力条件下,接收端实测波形如图4(b)、图4(c)所示。实验过程保持激励源不变,激发端及接收端传感器均布置在钢绞线端面,随钢绞线张拉力增大,钢丝间接触应力发生变化,实测导波波形幅值明显降低。

图4 实测导波信号Fig.4 Measured guided wave signals
对输出端波形进行去除均值和趋势项处理后,以激励波形和输出波形作为系统的输入和输出,采用ARX模型进行系统辨识。模型定阶是ARX模型估计过程中重要的一环,阶数的超定和欠定都会很大程度地影响模型的准确性。最小信息准则(Akaike information criterion,AIC)法是ARX模型定阶方法中相对成熟的信息量准则法,假设考虑某个含k(k≤p)个参数的参数模型,其密度函数记为g(y|θk),对应的似然函数最大值记为g(ˆθk|y),这里θk为未知参数,而ˆθk为其极大似然估计,则AIC准则定义为AIC=-2lng(ˆθk|y)+2k。式中第一项反映模型拟合的优良性,第二项表示对模型采用较多变量个数的一种“惩罚”,最终阶数的确定是权衡模型拟合效果与变量个数的结果。
对实测数据采用AIC准则法定阶,确定ARX模型的最佳阶次分别为na=10、nb=3,na、nb分别为ARX模型中多项式A(q-1)、B(q-1)的阶次。以式(14)所示单周期正弦脉冲为系统输入,(20%~70%)Fm荷载状态下实测数据为系统输出,建立ARX系统辨识模型参数如表2所示。

表2 不同张拉力下系统辨识模型参数Table2 Identification model parameters in different tension force
随钢绞线张拉力增大,系统模型参数发生了明显变化。总体而言,[a1,a2,···,a10]中各参数均呈规律性的单调变化,其中部分在增大,部分在减小,仅从参数的变化趋势无法判别钢绞线应力值。
为验证系统辨识模型的准确性,真实值与模型计算值的拟合度按式(15)计算:
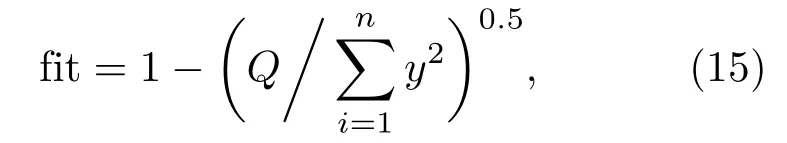
其中:残差平方和
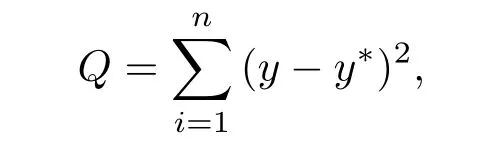
y为真实的输出值,y∗为根据系统模型计算的输出值。
以图4(a)所示波形作为系统输入,以70%Fm对应的[a1,a2,···,a10]作为模型参数,预测波形与真实波形如图5(a)所示,真实值与预测值之间的残差如图5(b)所示。图5(b)中所示残差分布比较均匀,绝对值不超过0.03,相对值约为3%,按式(15)计算拟合度fit=97.32%,说明模型定阶合理,拟合度较高,辨识结果可靠。

图5 辨识模型的拟合度Fig.5 The fit degree of identification model
4.2 钢绞线张拉力识别指标
实验过程共独立开展了6根钢绞线逐级加卸载实验,采用相同的模型阶数计算模型参数[a1,a2,···,a10],取6根钢绞线70%Fm状态下的平均值[¯a1,¯a2,···,¯a10]作为基准值,按式(13)计算张拉力指标Istf,结果如图6所示。
基于6组独立的钢绞线逐级加载数据构建的张拉力识别指标Istf随张拉力增大呈现出明显的单调变化规律。由于指标值Istf是以70%Fm作为基准值,荷载越小将产生更大的模型参数差异,从而识别指标值也将更大,所以关系曲线表现为负斜率。考虑到运营期结构的实际受力状态,实验数据没有考虑20%Fm以下的受力状态。
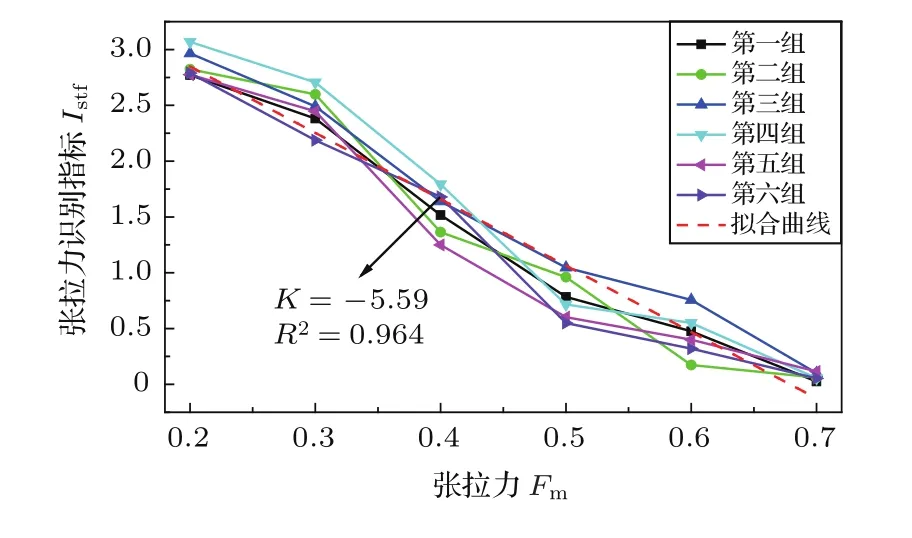
图6 识别指标随张拉力变化曲线Fig.6 The relationship curves between identi fication index and stress level
以识别指标值Istf为自变量,以钢绞线张拉力为因变量,建立钢绞线张拉力F随实测指标值Istf之间函数关系如下:
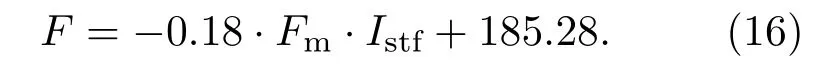
4.3 传感器布置位置影响
对单根高强钢丝而言,传感器布置在端面及侧面位置,实测波形中包含的纵波和弯曲波成分不同。钢绞线尚无导波传播的解析解,端面和侧面传感器实测波形成分不得而知,实验中分别在端面和侧面布置传感器分析传感器布置位置对应力识别结果的影响。相同荷载工况、相同激励源输入条件下,端面、侧面实测输出波形的识别指标Istf计算结果如图7所示。
由图7知,无论传感器布置在端面还是侧面,实测数据计算的识别指标Istf曲线表现出相同的单调变化规律。传感器布置在端面时,最小二乘法直线拟合k=-5.93,确定系数R2=0.984,传感器布置在侧面时k=-5.46,确定系数R2=0.933。相比较于侧面布置传感器,传感器布置在端面时,拟合直线斜率k值绝对值增大了8.6%,确定系数增大了5.5%。k值减小将使得在同样的应力变化条件下,识别指标值的变化更为明显。

图7 不同位置布置传感器时识别指标曲线Fig.7 Identification index curve at different sensors position
总体而言,传感器无论布置在侧面还是端面,采用基于ARX系统辨识模型参数的张拉力识别指标均能够反映钢绞线张拉力状态,且均具有较好的线性变化规律,当采用端面布置传感器将更能提高识别指标的敏感性和拟合度。
4.4 应力加载路径的影响
预应力结构承载能力检算只考虑钢绞线的状态应力,与钢绞线的加载路径无关,因此,张拉力指标值应尽量避免应力加载路径的影响。钢绞线逐级加卸载两个循环,激发同样的宽频单周期正弦脉冲,端面布置传感器,计算张拉力指标值Istf随加载等级变化如图8所示,直线拟合参数如表3所示。

图8 加卸载时识别指标曲线Fig.8 Identification index curve for loading and unloading process
由图8可知,钢绞线逐级加卸载两个循环,加载与卸载过程中识别指标Istf均呈单调的近线性变化规律,钢绞线的加载路径没有影响识别指标的规律性。比较两次加卸载循环k值变化,第1次加载与第2次加载、第1次卸载与第2次卸载之间k值变化均较小,分别下降了1.3%和0.9%。相对而言,两次循环各自的加卸载之间k值变化略大,分别下降了9.9%和9.6%,主要是受加卸载时液压滞后导致的读数差异所致。总体而言,重复加载时识别指标能够保持稳定,受加载过程的影响较小。
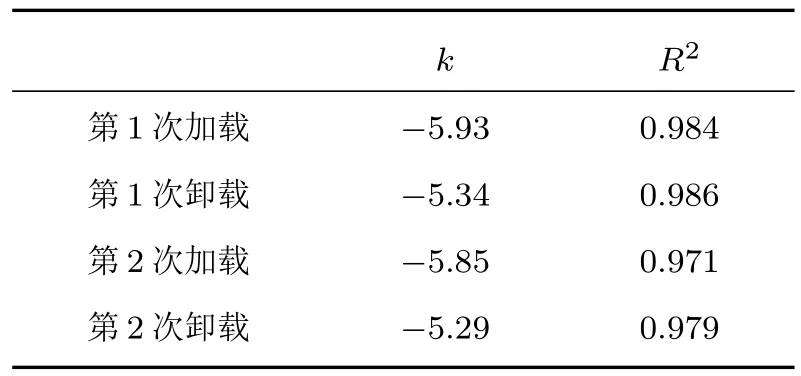
表3 直线拟合参数表Table3 Parameters of linear fitting
5 结论
(1)采用系统辨识方法能够有效识别钢绞线张拉力引起的系统导波传播特性变化,以ARX系统辨识模型参数作为特征向量,构建预应力钢绞线张拉力识别指标Istf,随钢绞线张拉力增大,指标值表现为明显的单调线性规律,按最小二乘线性拟合效果良好。
(2)基于端侧面实测导波数据的张拉力识别指标Istf随张拉力的增大均呈现出明显的单调线形变化规律,相对而言,端面布置传感器线性拟合k增大8.6%,确定系数增大5.5%,指标值的敏感性和拟合度更优。
(3)重复加卸载过程中识别指标具有良好的一致性,两次加卸载循环在加载阶段和卸载阶段直线k值分别下降了1.3%和0.9%,识别指标受加载路径的影响较小。
