小波包节点分段阈值降噪在水声监听中的应用∗

赵 杰 杨 英123 惠 力123 王 志123 初士博123 刘茂科123

(1齐鲁工业大学(山东省科学院) 济南 250353)

(2山东省科学院海洋仪器仪表研究所 山东省海洋环境监测技术重点实验室 青岛 266061)

(3国家海洋监测设备工程技术研究中心 青岛 266061)

0 引言

目前，水声监听在海洋生物调查研究、舰艇监听监测、深海勘探等方面需求量具大且应用前景十分广阔，其监听信号主要为宽带中低频信号和窄带高频信号，如鱼类的摩擦声频率一般在100 Hz～8 kHz，鱼鳔发声多数在75～100 Hz；舰船噪声谱主要集中在1 kHz以下；水声场测量、海洋地震测量、浅地层剖面测量等主要采用宽带中低频进行测量，频率范围在几百Hz到十几kHz；侧扫声呐及地貌扫描声呐等采用窄带高频信号，频率范围在十几kHz到几百kHz。在实际的水声探测、接收和识别过程中，海洋环境噪声信息会弱化相关声目标信号监听的准确度[1-2]，严重影响目标的后续识别与处理，特别是宽带中低频目标信号更容易掺杂大量复杂的噪声信息。因此，如何将目标信号与噪声有效分离与提取成为水声监听研究的重中之重。

传统的数字信号处理及去噪方法多数是以傅里叶变换为基础的，如司新新等[3]利用短时傅里叶变换进行时变和非平稳信号的处理和分析，姚家骏等[4]在地震波特征量分析中采用短时傅里叶变换，曲丽荣[5]选用合适的短时傅里叶窗口函数对信号频率特性分析。以上研究均以傅里叶变换为基础的传统数字信号去噪法属于全局变换，无法同时表征时频双域特性，只能反映信号整体特性，时域无法局部化，难以检测局部突变信号，去噪局限性较大。小波变换去噪方法具有良好的时频局部性、多分辨率、去相关性、快速算法和选基灵活等特点，与傅里叶变换去噪方法相比具有明显的优越性，成为国内外许多学者专家应用研究的去噪方法。Kalpana等[6]对水声通信中提高信噪比的去噪技术进行研究，利用Gabor小波变换来实现去噪提高信噪比，并与香农小波进行了对比研究。Hill等[7]使用双数复小波系数法实现图像噪声处理研究。普利达大学研究人员Ghribi等[8]提出用小波变换分解的双线性结构，通过双通道对称方法实现小波自适应去噪声。周建等[9]利用一种新的小波阈值去噪方法对振动信号进行去噪分析。张振凤等[10]利用改进阈值随实际分解层数而变化的方法进行去噪，通过信噪比和均方差的比较，该方法优于传统固定阈值、stein无偏似然估计阈值、极大极小值的小波去噪方法。曹建华等[11]利用小波分析法对振动信号进行去噪处理，对去噪后信号进行功率谱密度分析。余本富等[12]基于自适应分解层数和阈值的小波去噪算法降低电能质量扰动信号中的噪声。李战明等[13]对小波分析中4种去噪方法分析比较，通过对比分析采用改进阈值函数提升小波变化阈值法用于心电信号去噪分析。以上小波变换的研究方法在阈值和阈值函数选取等方面具有较高的参考价值，但其主要针对频率变化缓慢和频带较窄的非平稳振动、心电等生物医学、图像处理等方面信号，不能同时兼顾低频和高频目标，无法实现宽频带信号分频段聚焦处理，因此，对频段变换范围较大的水声监听信号消噪及提取处理适应性较差。

水声信号属于非平稳、非线性时变信号，受噪声及混响等干扰的影响，探测获得的水声信号往往会存在很多突变的奇异点。小波变换具有多分辨和时频局部分析的能力，与短时傅里叶去噪法相比，能更好地去噪，小波和小波包降噪处理的核心是阈值和阈值函数的选取，常用的小波硬阈值和软阈值函数达到了一定的去噪效果，但硬阈值处理后的小波系数在正负阈值处不连续，软阈值可有效避免间断连续性较好，但小波系数较大时，系数绝对值与系数之间存在偏差，易造成高频信息损失，重构信号易产生误差。小波包分解系数按照不同的阈值规则能更有效去除噪声，然而不同频段的小波包分解系数对目标信号和噪声信号反映不同，用同一阈值和阈值规则对整个频段进行处理无法达到较为理想的效果。因此，本文采用小波包相对能量法进行最优分解层判别，考虑各个节点频段有用信息的比例，按照比例大小确定阈值准则及函数，进一步提高分辨率，优化高频信号分析，去噪提取结果更加精细优化。利用小波包节点系数分段阈值处理的方法对监听获得的100 Hz～50 kHz范围内水下声音数据降噪处理分析，对不同频段范围内的水声信号进行提取，噪声信号分离，结果表明：该方法既可以对1 kHz上下范围内的较强信号进行降噪提取，也可对较高频率相对较弱的信号实现降噪分离。

1 小波包算法基本原理

小波包算法为最佳子带树结构(Optimal subband tree structuring)，包括分解算法和重构算法。用子带树来表示小波包分解，利用多次迭代的小波转换对信号的低频和高频部分进行多层次划分，根据信号特征，自适应选择频带范围，分析信号细节部分。小波包克服了小波分析的高频分辨率低的缺点，对信号在全频带范围内进行正交分解，提高时-频分辨率[14]。子带树结构图如图1所示。

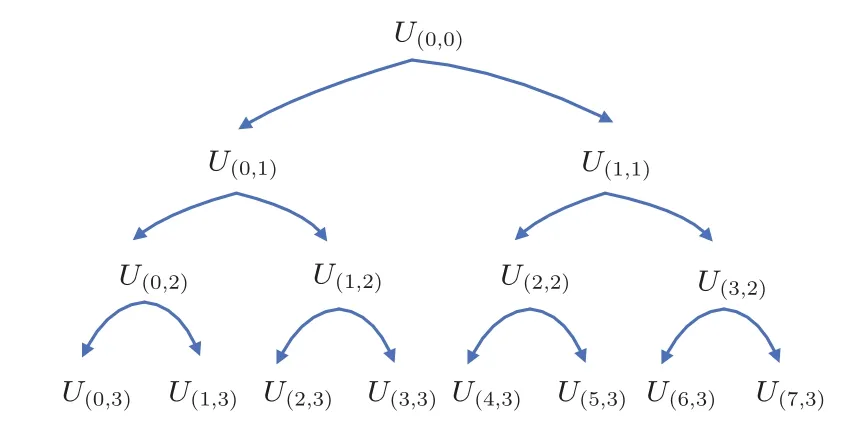
图1 子带树结构Fig.1 Subband tree structure

将尺度空间Vj和小波子空间Wj统一用U(n,j)新的子空间来表示：

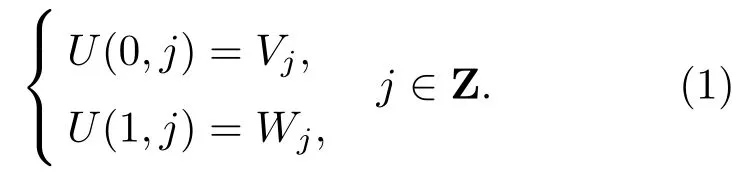
定义子空间U(n,j)为函数Un(t)的闭包空间，Un(t)是函数U2n(t)的闭包空间，令Un(t)满足双尺度方程：

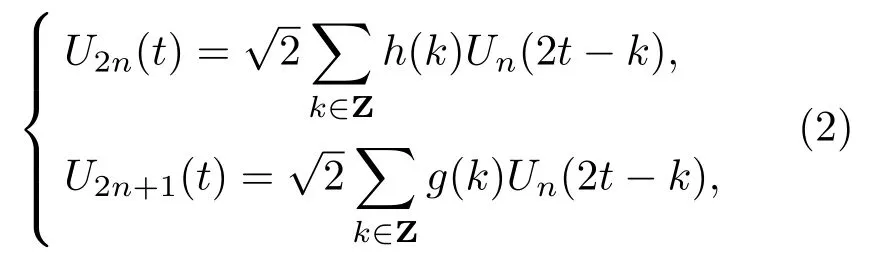
式(2)系数为多分辨率分析中的滤波器系数，满足正交关系，g(k)=(-1)kh(1-k)。当n=0，

在多分辨率分析中，U0(t)和U1(t)分别退化为尺度函数φ(t)和小波基函数ψ(t)：

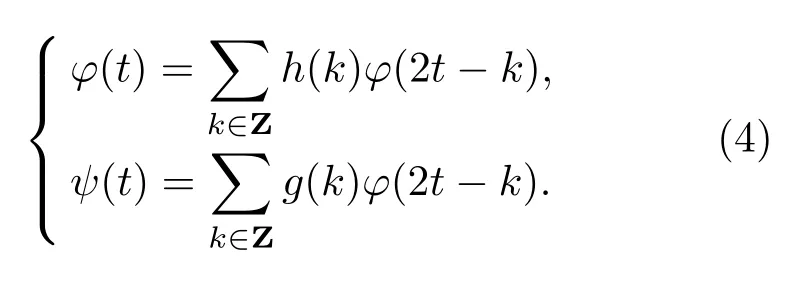
小波包变换的分解与合成中，存在由多种小波基组成的基底库，因此需要根据不同场合、不同信号并且在综合考虑小波基的正交性、紧支性、对称性等特性的基础上选择合适的小波基。从小波库中寻找使代价函数最小的小波包基，选择关键是代价函数[15]。

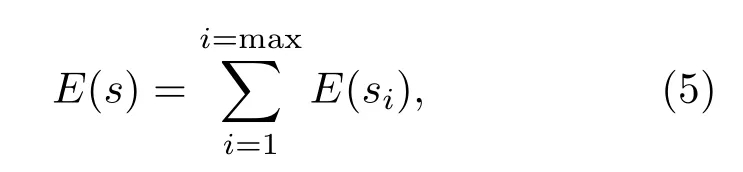
式(5)中，s代表信号，si表示信号在小波包基上的分解系数。求出使代价函数最小的小波包序列，从而求出最优基。代价函数称为熵或平均信息量，代价函数自变量是信号在某个基向量组上分解系数，函数实部因变量即为代价。采用二叉树自下向上搜索最优小波包基，小波包基的选取是后续数据处理的关键。

1.1 小波包相对能量确定最优分解层数

小波包分解需要获得一个最优的分解层数。分解层数直接影响信号的去噪效果，分解层数过多对各层小波系数阈值处理过程中造成信息量丢失严重、信噪比下降、运算量增加。分解层数过少，信噪比提高不多，去噪效果不明显[16]。原始信号和噪声信号的小波系数在不同层次有不同特性，原始信号的小波系数会随着分解层次增加而增大，噪声信号小波系数减小。

通过最优小波包中节点能量判断的方法确定小波包分解层数。根据最优小波基节点能量的大小，判断该节点有用信号能量大小。能量越高，表示该频段的有效成分越多，反之，噪声成分越多。据此，根据能量值判断有效成分，确定最优分解层数。

如图1所示，U(i,j)表示第j层的第i个节点，每个节点系数表示某一频段内的信号特征，其中j=0,1,···,n，i=0,1,···,2j-1。能量计算公式为[17]

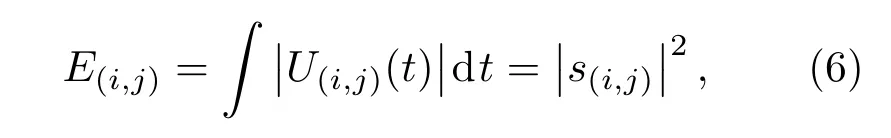
式(6)中，s(i,j)为U(i,j)节点的小波包系数。由此可得出每层分解后子带的相对能量公式为

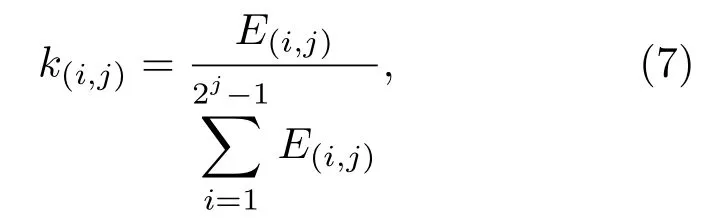
其中，k(i,j)为节点i在第j层的相对能量，代表有效成分的含量，对每层的节点相对能量k(i,j)由大到小进行排序，k(i,j)的最大值记为C(1,j)，最小值记为C(n,j)，即C(1,j)≥C(2,j)≥···≥C(n,j)，其中j代表层数。首先对信号第一层分解相对能量进行初判：C(1,1)≥0.9、C(2,1)＜0.1信号能量频段相对集中的情况，这种情况下对每层的k(2,j)进行对比，当第j层的C(2,j)大于第j-1层C(2,j-1)时，将j-1作为最优分解层数。

其他情况下，对信号逐层分解，将C(1,j)首次小于0.2的层数j进行记录，如果j＞1，最优分层数为m=(j-1)；如果j=1，最优分解层数为1。

1.2 小波包分段阈值处理法

水声信号的频率范围比较广，不能简单地将低频段作为有用信息、高频段作为噪声信号处理，按小波相对能量法实现分段阈值降噪处理，该方法与单一阈值处理相比充分考虑信号频率段与噪声分布情况。针对不同的分解系数选取最合适的阈值函数和阈值th，最大程度去除噪声，保留有效成分[18]。目前，常用的阈值估计方法主要有以下几种：

(1)固定阈值估计法(sqtwolog)，在正态高斯噪声模型下，针对多维独立正态变量分布得出的结论。

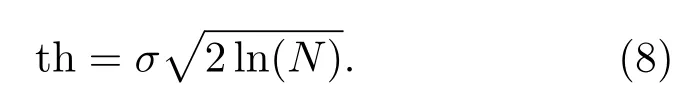
(2)无偏似然阈值估计法(rigrsure)，小波分解系数的平方记为λ，从小到大的顺序排列，即λ1≤λ2≤···≤λn。设风险向量R，其元素为ri，

风险向量R的最小值rmin作为风险值，对应求出对应的λmin，则阈值为

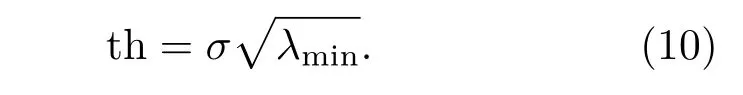
(3)启发式阈值法(heursure)，是前两种阈值的综合，设S为N个小波系数的平方和。令

(4)极大极小阈值法(minimaxi)，也是固定阈值的一种，产生最小均方误差的极值。

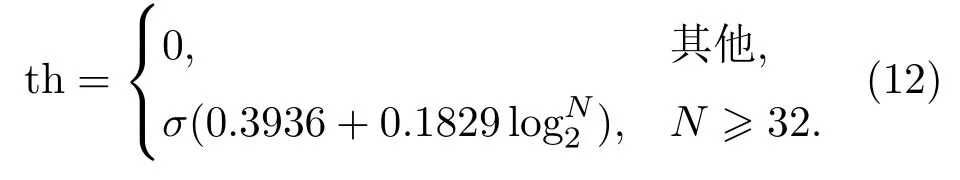
以上各式中σ=MAD/0.6745为噪声标准方差，MAD为各高频子带系数的中值；N为信号长度。

如1.1节所述，若C(1,1)≥ 0.9、C(2,1)＜0.1信号能量频段相对集中，只对C(1,1)≥0.9进行小波去噪。其他情况下，信号最优分解层m上，节点相对能量k(i,j)≥0.2的节点系数采用无偏似然估计阈值估计方法；k(i,j)≥0.1、k(i,j)＜0.2的节点系数采用极大极小阈值法；k(i,j)＜0.1的节点系数采用统一阈值法选择。多阈值准则选取表如1所示。

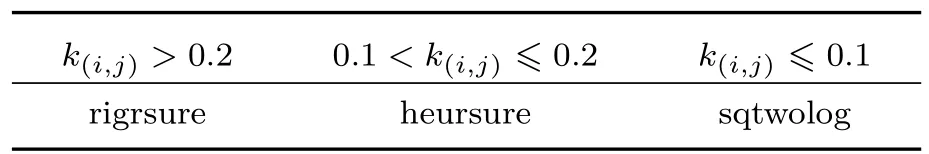
表1 多阈值准则选取表Table1 Multiple threshold criteria selection table

目前常用的阈值函数为硬阈值函数和软阈值函数。硬阈值将绝对值不大于阈值的元素置零，存在不连续现象，数学表达式为

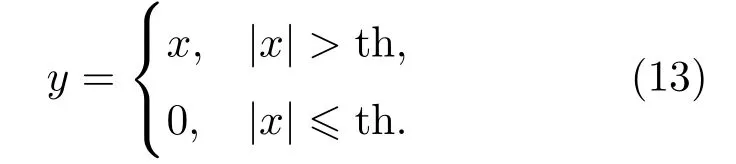
软阈值函数在式(13)的基础上实现连续点收缩为零，有效避免间断，连续性较好，但小波系数较大时，系数绝对值与系数之间存在偏差，易造成高频信息损失，重构信号易产生误差，其表达式为

考虑到硬阈值和软阈值函数处理信号细节成分的局限性，利用文献[19]中的新型阈值函数，公式如下：

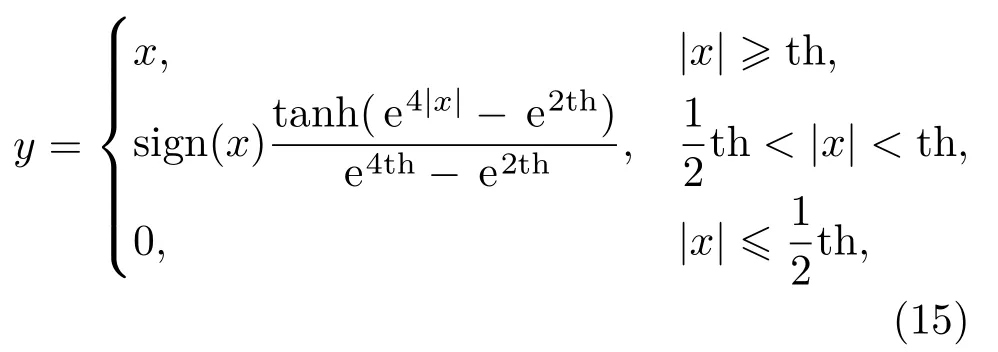
式(15)中，x表示小波包分解后的节点系数，y为阈值函数处理后的小波节点系数，th为选定的阈值。式(14)和式(15)中sign(x)为符号函数，当x＞0，sign(x)=1；当x=0，sign(x)=0；当x＜0，sign(x)=-1。阈值函数处理结果对比如图2、图3所示。

图2 软、硬阈值函数结果对比Fig.2 Comparison of soft and hard threshold function results

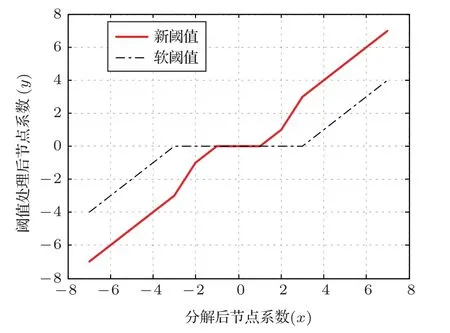
图3 新、软阈值函数结果对比Fig.3 Comparison of new and soft threshold function results

2 监听水声信号去噪分析

监听水声信号来源于阿拉斯加费班克大学Erin Pettit和华盛顿大学JeffNystuen等在阿拉斯加州冰湾利用自主水听器(被动水听器(PAL))获得的被动水声记录[20]，该海域的水深为160 m，水听器的布放水深为90 m。所有数据采样频率为100 kHz，从100 Hz～50 kHz共分为64个频段，其中100 Hz～3 kHz的范围内的频率分辨率为200 Hz，3 kHz～50 kHz范围的为分辨率为1 kHz。读取2009年某一时间段内的原始音频文件，其时频特性标度图如图4所示。

由图4的时-频域分布标度图可以看出原始水声监听信号频率随时间变化的强弱分布，本文的主要工作是对不同频段范围、不同强弱的信号进行消噪并且提取。将最原始水声监听信号按db6进行小波包分解计算，计算每层节点相对能量并由大到小排序(每层节点仅排前四位)，如表2所示。根据每层节点相对能量的大小按照1.1节判别方法获得最优分解层数为5层。按小波包5层将水声信号分解，进行最优树结构和节点系数频率大小排序，分别如图5和图6所示。的方式实现消噪分离，处理后时-频域标度分布如图7所示。依此频段来进行本文方法与全局单一阈值对比，将小波包硬阈值、小波包软阈值在5层分解的基础上对信号进行消噪处理，获得的时-频域信号分布图，分别如图8和图9所示。由图7、图8和图9三幅图片对比可以看出，本文方法具有良好的优越性。

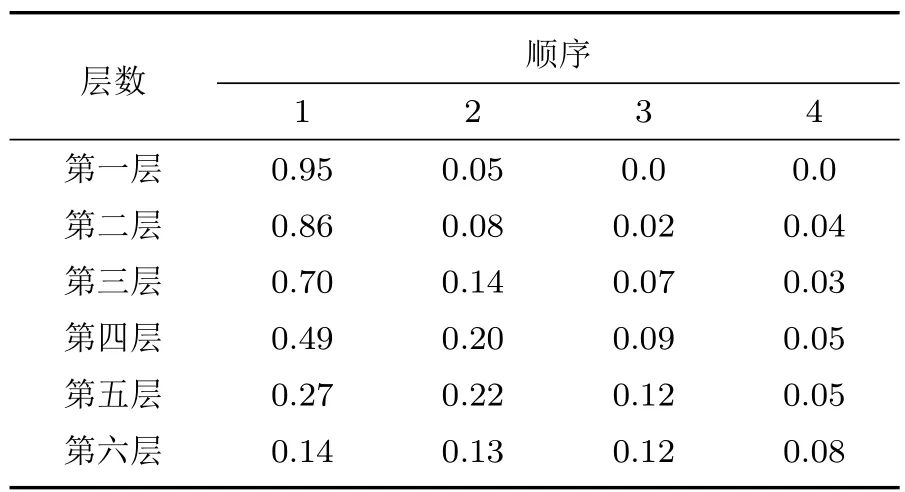
表2 节点相对能量排序表Table2 Nodes relative energy ranking table

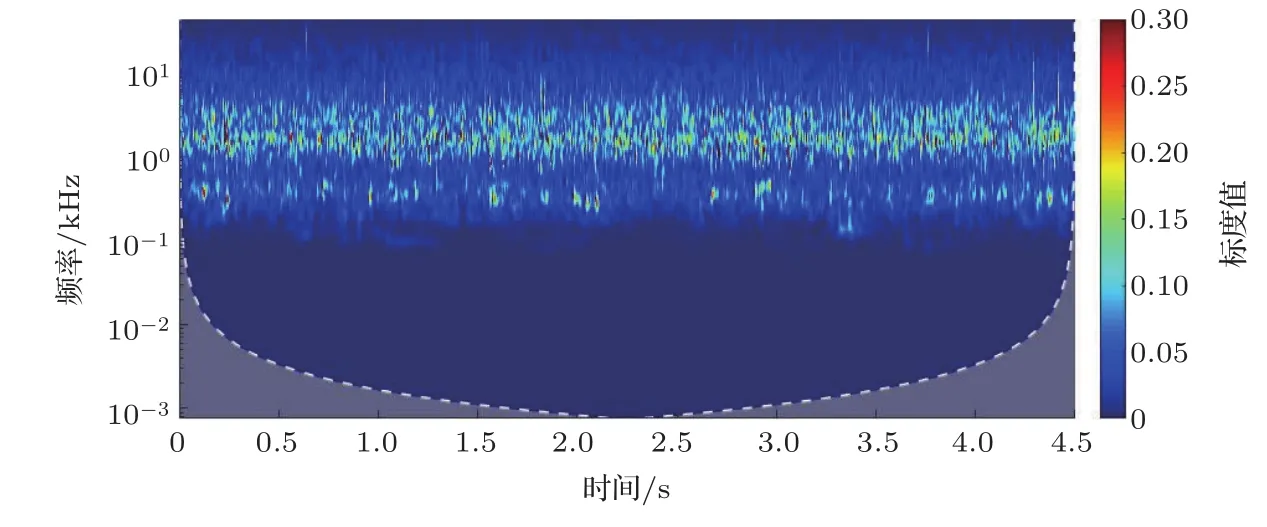
图4 监听水声信号时-频分布标度图Fig.4 Time-frequency distribution scale diagram for monitoring underwater acoustic signals

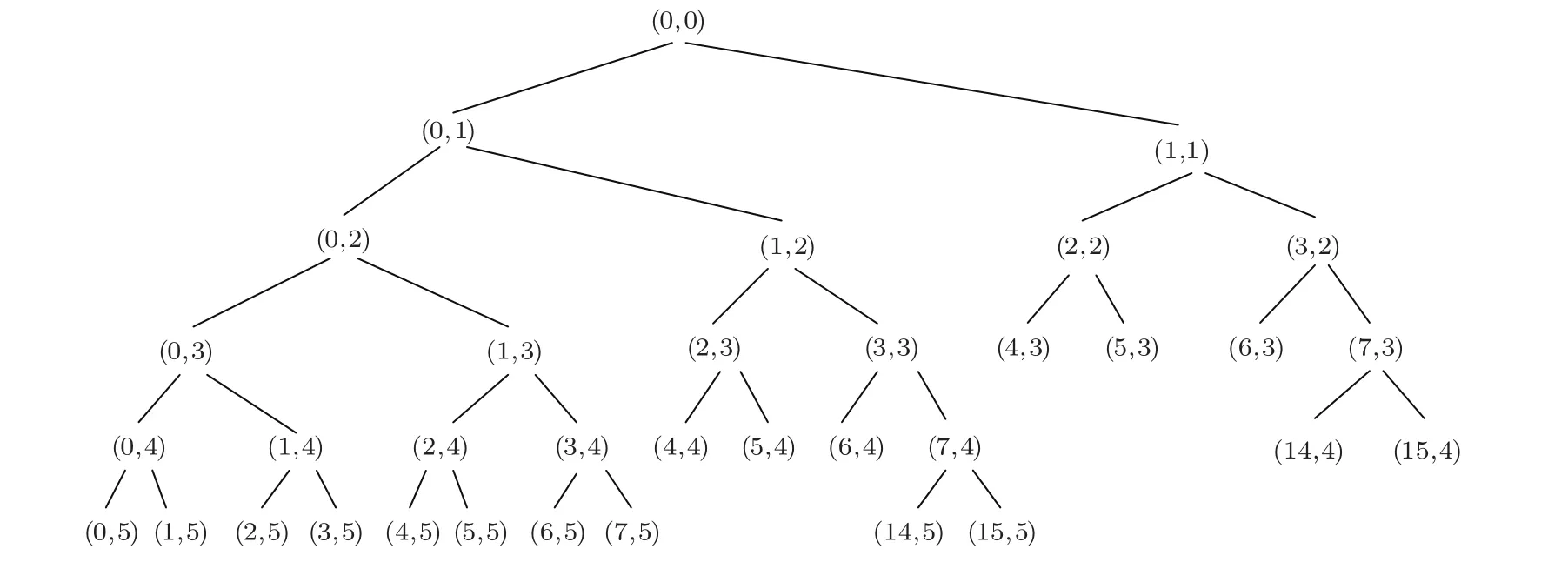
图5 最优树结构Fig.5 Optimal tree structure

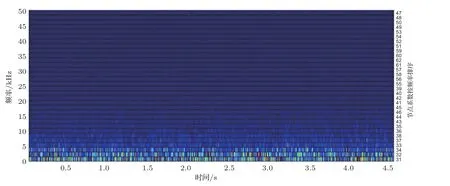
图6 节点系数频率排序图Fig.6 Node coefficient frequency sorting diagram

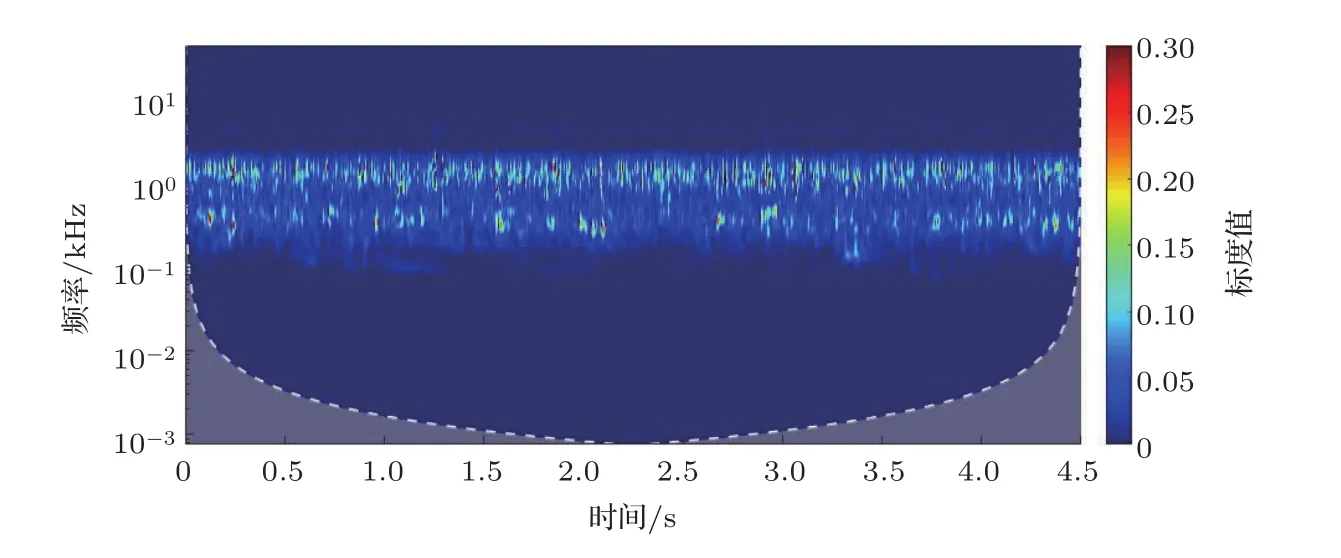
图7 分段阈值降噪信号时-频分布标度图Fig.7 Time-frequency distribution scale diagram of segmental threshold denoising signal

图6中横轴为时间，左边纵轴为频率大小顺序，右边纵轴为小波包分解第五层节点系数31-62按照频率顺序由下往上进行排序。由图6可看出监听水声信号频段主要分布在31、32、34三个节点上，频率范围在0～5 kHz。通过本文方法，首先对频段在节点31处监听水声信号，频率范围大约在0.1 kHz～1.6 kHz，按照节点系数分频段阈值处理

图8 硬阈值降噪信号时-频分布标度图Fig.8 Time-frequency distribution scale diagram of hard threshold denoising signal

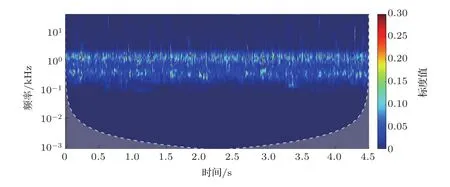
图9 软阈值降噪信号时-频分布标度图Fig.9 Time-frequency distribution scale diagram of soft threshold denoising signal

图7为利用本文方法的消噪提取结果，信号提取结果较为理想，噪声基本消除。图8中为小波包硬阈值5层分解处理后的监听水声信号时-频域标度分布图，与图4原始信号相比，信号降噪较为明显，但依然存在噪声。图9为小波包软阈值降噪处理，与图8相比，噪声频率信号进一步减少，但降噪不够彻底，仍存在小部分噪声。小波包分段阈值降噪分离的关键在于在未知真实有效的水声信号前提下，节点系数按频率排序，节点系数频率由低到高、信号强度由强到弱的排序为31、32、34、33、37，其频率范围大约在0.1 kHz～1.6 kHz、1.7 kHz～3.3 kHz、 3.4 kHz～5 kHz、 5.1 kHz～6.7 kHz、6.8 kHz～8.4 kHz，按照本文方法对剩余4个节点频率信号进行提取，其消噪提取结果较为理想，结果如图10～13所示。由图12、图13可以看出频率范围相对较高、信号强度较弱的节点33、节点37的信号消噪提取亦可通过本文方法实现。

由于监听的真实水声信号未知，参照文献[21]平滑度指标、信噪比增益和峰值信噪比三种方法对监听水声信号进行去噪评价。三种方法的定义及公式表示如下：

(1)平滑度指标是指去噪后的差分数的方差根和原始信号的差分数的方差根之比，记为r，

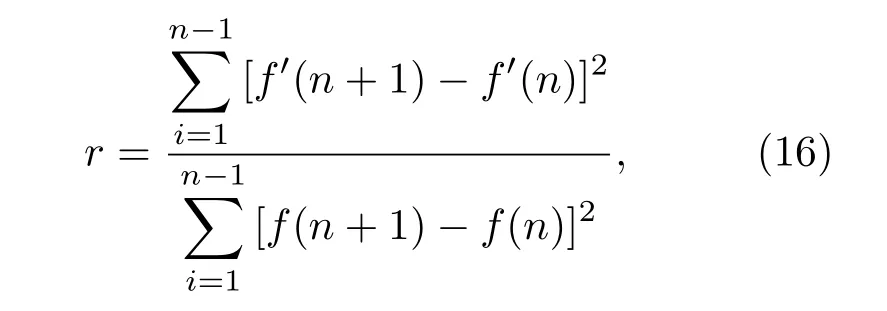
其中，f′(n)为去噪后函数，f(n)为原始信号。

(2)信噪比增益是指去噪后的信噪比和去噪前的信噪比的比值，记为GSNR，

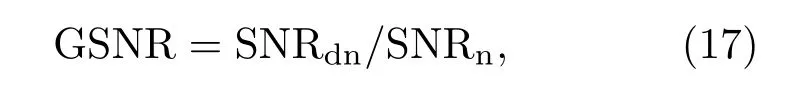
其中，SNRdn为去噪后信噪比，SNRn为原始信号信噪比。

(3)峰值信噪比信号最大可能功率和影响它的表示精度的破坏性噪声功率的比值，记为PSNR，

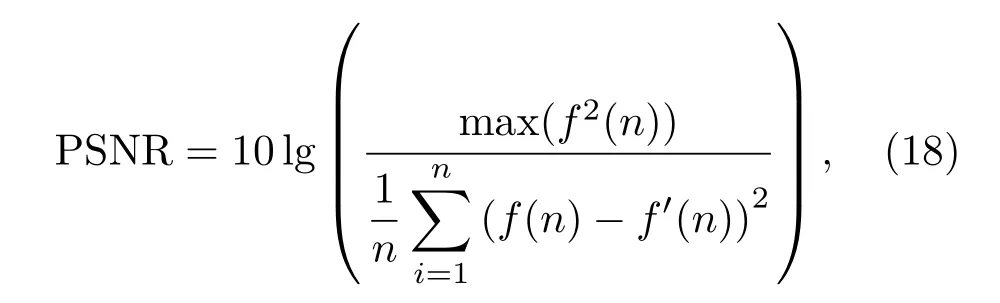
其中，f′(n)为去噪后函数，f(n)为原始信号。

图10 节点32频段降噪信号时-频分布标度图Fig.10 Node 32 time-frequency distribution scale diagram of segmental threshold denoising signal

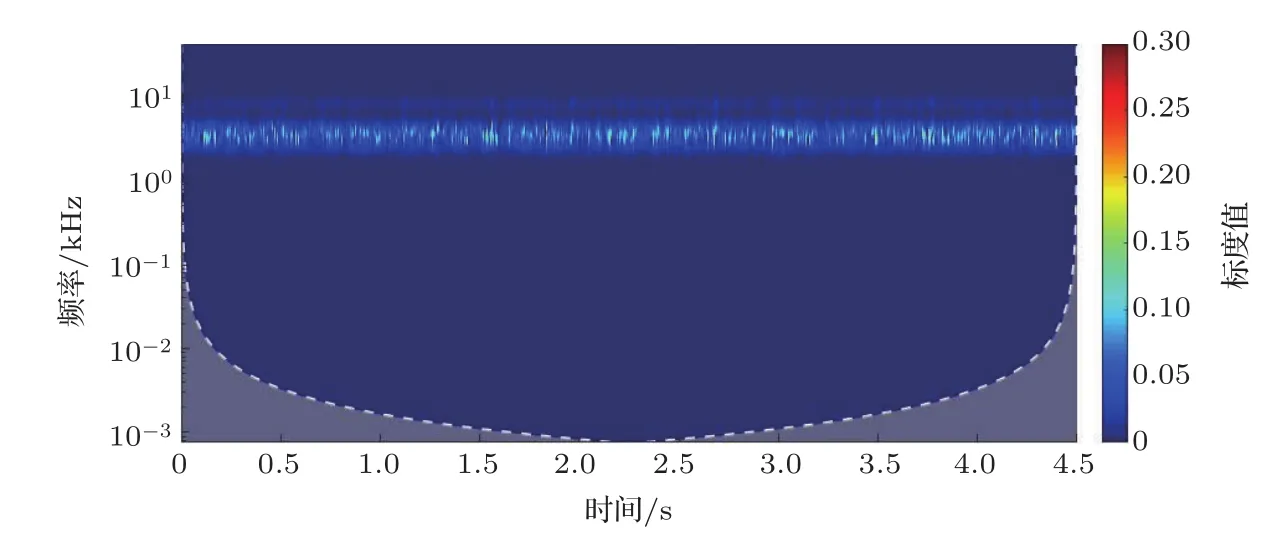
图11 节点34频段降噪信号时-频分布标度图Fig.11 Node 34 time-frequency distribution scale diagram of segmental threshold denoising signal

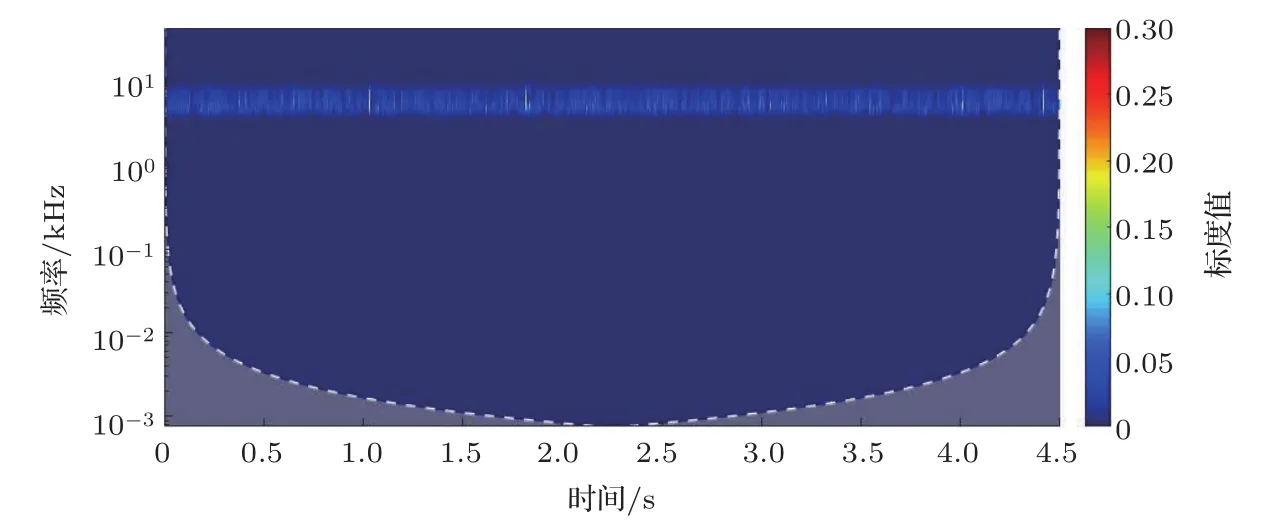
图12 节点33频段降噪信号时-频分布标度图Fig.12 Node 33 time-frequency distribution scale diagram of segmental threshold denoising signal

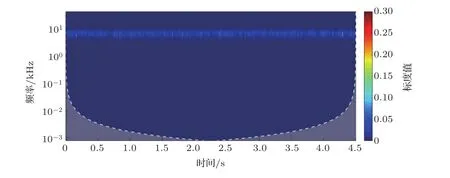
图13 节点37降噪信号时-频分布标度图Fig.13 Node 37 time-frequency distribution scale diagram of segmental threshold denoising signal

平滑度指标数值越小，信噪比增益和峰值信噪比越大，去噪效果越好。表3是采用上述三种方法分别对小波包硬阈值，小波包软阈值和小波包分段阈值的降噪处理结果进行去噪评价，由表3可以看出本文方法是可靠的。

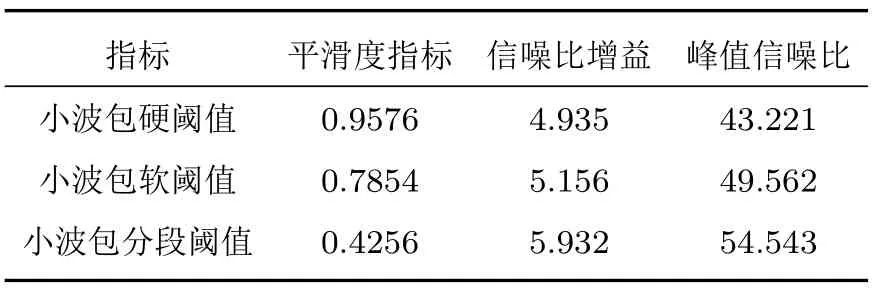
表3 评价结果Table3 The evaluation results

3 结论

通过对水下监听信号的去噪分析可以得出本文方法的关键在于(1)按照每层小波包节点系数相对能量的变化确定小波包最优分解层数；(2)按相对能量法实现分频段阈值降噪处理。根据节点相对能量大小，判断该节点有用信号能量大小。能量越高，表示该频段的有效成分越多，反之，噪声成分越多。针对节点系数相对能量大小选取最合适的阈值函数和阈值th，最大程度去除噪声，保留有效成分。本文方法去噪效果优于传统小波、小波包全局单一阈值处理等方法，可在信号噪声的处理中进行广泛的推广和应用，特别在100 Hz～50 kHz频率范围内的水声监听信号降噪处理中具有重要参考价值。