ECDLP问题中的点乘优化算法和Pollard-rho算法仿真研究*

郭士增

（哈尔滨工业大学，黑龙江 哈尔滨 150001）

0 引 言

基于椭圆曲线密码体制的多方认证密钥协商协议即为多用户之间协商并加入身份验证这一机制的密钥协商协议，当今可将区块链存储技术思想应用于基于椭圆曲线的多方密钥协商协议方案。首先针对基于区块链存储的多方认证密钥协商协议进行协议有效性和可靠性的分析，其次对协议有效性提升提出了优化的点乘算法，并在协议可靠性验证上针对密钥体制安全性仿真分析了Pollard-rho攻击算法，估算了破解时间。

1 多方密钥协商协议有效性与可靠性衡量

衡量多方认证密钥协商协议的有效性指标为通信轮数、计算次数和计算量。计算量这一指标在某些有效性要求高的场景下会用通信时延来代替。文中采用计算量的衡量方法。

通信轮数：2轮。第一轮为用户Ui与用户{Ui-2,Ui-1,Ui+1,Ui+2}进行通信，向用户{Ui-2,Ui-1}处发送消息，从用户{Ui+1,Ui+2}处接收消息。第二轮为与服务器进行通信，发送消息(mi´,Sigi(H(mi´)))，接收消息(mi´´,Sigi(H(mi´´)))。该协议通信轮数为2，属于较少轮数的协议，满足场景要求。

计算次数：单个普通用户（排除验证节点）的计算次数为4，分别为协议第一轮中计算Zi的1次点乘计算、第二轮中计算αi中的2次点乘计算和1次安全单向函数的计算。

计算量：计算量指标是指根据相关文献结论，对基本运算计算复杂度的估计。设求逆元运算的复杂度为I，乘法运算复杂度为M，平方运算复杂度为S，设密钥长度为l，可得出3次点乘计算量约为4lI+8lM+7lS，而安全单向函数在仿真中使用平方取中法，计算量仅有1次平方运算。因此，可以认为计算量为4lI+8lM+7lS。

多方认证密钥协商协议的可靠性要求大多采用已知密钥安全性、完美前向保密性、密钥不可控制性、抵抗密钥泄露攻击、密钥共享可知性、会话密钥托管（SessionKey Escrow，SKE）、密钥值偏移攻击（Key Off-set Attack，KOA）、抵抗中间人攻击（Man-in-the-middle Attack Resilience，MITM） 和防重放攻击等标准衡量。

已知密钥安全性：攻击者通过已知的过去的密钥无法得到新会话密钥。因为在本协议中每个用户都会在第一轮产生随机数作为短暂的私钥，因此每次最终产生的密钥是唯一的。由于该私钥在一次会话结束后立即被舍弃，攻击者通过已知的过去的密钥无法得到新会话密钥。

完美前向保密性：一个用户或多个用户长期使用的私钥被泄露，对于该私钥泄漏前生成的会话密钥不产生影响。由于本协议除数字签名外不会使用长期私钥，每次生成密钥的过程中都会使用新的随机数作为私钥，因此不会导致之前的会话密钥泄露。因此，本协议满足完美前向保密性。

密钥不可控制性：参与群组通信的不同用户都不能对协商的会话密钥预先控制为特定值。本协议虽然有验证节点和服务器这种与普通用户权限不同的节点参与密钥协商，但各方都不能对协商最终产生的会话密钥预先控制。最终密钥包含每个用户节点产生的短私钥信息，具有随机性，不可预先生成。

抵抗密钥泄露攻击：假设用户A的私钥长期泄露，那么攻击者能够假扮用户A欺骗其他用户，但不能扮演其他用户去欺骗A。由于本协议在用户与用户之间和服务器之间都采用了数字签名技术，而且每次通信均由验证网络进行身份验证，因此防止了攻击者已知Si情况下的密钥泄露攻击。

密钥共享可知性：协议在全体用户知晓下才能进行，任一或多个参与者不知晓的情况下，都不能进行密钥协商协议。根据协议本身网络结构与过程可知，每个用户与相邻的4个用户进行通信，而联盟链场景下成员间相互信任并知晓成员数量和某些身份信息，因此在计算中如果跳过某成员，那么它相邻的成员在通信时会察觉出某用户不知晓的情况，此时该协议停止。

会话密钥托管SKE：通过监听协议参与者在协议运行过程中的通信过程，根据已有消息以及通信过程获得的消息，可以恢复该次协议运行产生的会话密钥。根据本文提出的协议，服务器可通过累加得到最终密钥。但是，由于第三方中心每次通信时都需经过验证网络验证，因此一旦第三方可信中心利用最终密钥作恶时，验证网络可知晓其行为异常，且记录在系统账本中，可终止服务器与用户间的通信，防止其继续做恶。

密钥值偏移攻击KOA：该攻击是指攻击者拦截并篡改通信参与者之间交互的信息，使通信参与者最终计算出的密钥值是错误的。如果协议可以避免这种情况的发生，则称该协议能够抵抗密钥值偏移攻击。因为在本协议的通信过程中，每次信息都会包含散列值与数字签名，因此一旦篡改密钥或信息都会改变散列值进而改变签名，随后验证网络察觉异常并被信息接收者知晓。本协议满足该指标。

抵抗中间人攻击MITM：中间人攻击是指攻击者与通信的参与方分别建立独立的联系，并交换所收到的数据，使通信的参与者认为他们正在通过一个私密的连接与对方直接对话，但事实上整个会话都被攻击者完全控制。由于用户间通信需要进行数字签名及身份验证，如在第一轮中用户与相邻用户进行通信的过程中使用了数字签名，在中间人不知道用户数字签名的私钥的前提下，中间人无法伪造用户的数字签名，因此不能进行中间人攻击。若中间人在用户通信开始前已经控制了双方通信过程，即同时伪造两个身份与双方通信，此时中间人使用自己的私钥并发给用户对应对方的伪造公钥。由于用户事先在服务器（或可信第三方机构）注册密钥对中的公钥，因此在基于PKI体系认证中其他用户会根据服务器发送的证书得知该用户可信合法的公钥，从而知晓中间人的签名与用户签名不同而终止协议。而在身份认证中，其他用户预先知晓用户的合法公钥，中间人的攻击同样不会奏效。

防重放攻击：重放攻击是指攻击者把截取到的以前消息再次发送给接收者，以此使接收者认为其正在通信。由于每次通信中消息都加入了时间戳，因此使用之前的消息进行攻击会与用户解密出的消息时间戳不同，从而使用户发觉被攻击而终止协议。

根据上述分析，公网-专网联盟场景下对于多方密钥协商协议可靠性满足密钥共享可知性；对于每次生成消息的数字签名和散列值可防止任意一个成员否认或纂改，满足完美前向保密性；监听者只监听用户之间的消息，那么监听者只能得到第一轮中的消息而无法得出最终生成的会话密钥，满足密钥不可控制性；因为第一轮消息的保密性是基于椭圆曲线上的离散对数问题（Elliptic Curves Discrete Logarithms Problem，ECDLP）问题难解，即抵抗中间人攻击，协议满足抵抗密钥泄露攻击要求指标。综上所述，给出的方案满足该场景下的可靠性要求。

2 椭圆曲线加密攻击Pollard-rho算法

在公网-联盟链情形下的多方认证密钥协商协议的一般场景，每个用户的私钥的破解是攻击算法的目标[1]。根据椭圆曲线基本原理，从程序实现角度，将n次点加运算累加引入数据乘2的运算，降低了运算次数。而对于ECDLP问题，尚未发现有效的亚指数级计算复杂度的一般攻击方法，且ECDLP的攻击算法大多只针对特定椭圆曲线有效[1]。因此，研究针对阶数为合数与素数的椭圆曲线进行攻击的一种Pollard-rho算法，对于存在较小阶n椭圆曲线的ECDLP问题进行求解，分析基于椭圆曲线加密的密钥协商协议可靠性。假设ECDLP问题中椭圆曲线参数如下：素数p，椭圆曲线E，椭圆曲线参数a、b，基点P，阶为n，椭圆曲线上另一点Q，其中Q=kP，k为常数。对于ECDLP求解问题，已知P、Q，求解k。

2.1 点乘优化算法

假设Q=kP，阶数n。求解的问题为：已知P、Q，求解k。

点乘运算和点加运算是椭圆曲线密码体制的基本运算，一般把点乘运算分为多倍点运算和2倍点运算。两种优化算法都是基于2倍点运算和点加运算的点乘算法。最基础的点加运算和2倍点运算可按式（1）和式（2）进行计算。

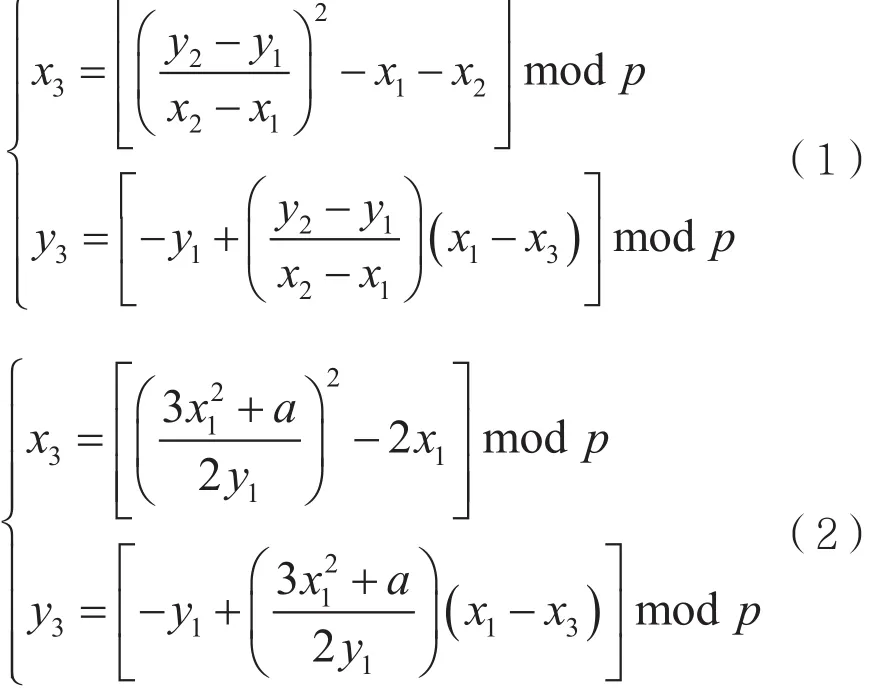
对于基本运算计算复杂度的估计，可推出表1。

表1 基本运算的复杂度

两种点乘的优化算法分别为二进制展开法和加减法，这里给出加减法算法。

本算法原理是3k和k对应比特不同时说明低位有进位从而计算k。利用这一过程直接进行点加操作，从而求出kP。其中，Q-P的运算是通过Q+(-P)实现的。假设P(x,y)，定义-P(x,-y)。

第一步，将倍数k和3k转换为二进制数，k为krkr-1…k1k0，3k为hrhr-1…h1h0，其中3k的最高位为1，同时创建Q[1][2]数组存储Q点坐标；

第二步，置Q为点P，i为r-1（i为循环变量）；

第三步，Q=2Q，将坐标存入数组对应位置；

第四步，（1）若hi=1且ki=0，则Q=Q+P；

（2）若hi=0且ki=1，则Q=Q-P；

（3）将坐标存入数组对应位置；

（4）i-1；

第五步，判断i是否小于1，若是，输出Q坐标；否则返回第三步。

图1为加减法算法流程图。

图1 加减法算法流程

计算多倍点乘运算，设k的比特数为l，k的码重为W。二进制展开法需要l-1次2倍点运算和W-1次点加运算；加减法需要l次2倍点运算和l/3次点加运算。设求逆元运算的复杂度为I，乘法运算复杂度为M，平方运算复杂度为S，

由于k具有随机性，一般有W≈l/2，可得到二进制转换法计算复杂度为1.5lI+3lM+2.5lS，加减法算法计算复杂度1.33lI+2.67lM+2.33lS。加减法比二进制转换法计算复杂度低，因此加减法在时间复杂度要优于二进制转换法[2]。

2.2 Pollard-rho算法

假设Q=kP，阶数n。求解的问题为：已知P、Q，求解k。Pollard-rho算法的思想是将循环群分为不同子群，循环群的行走路线像一条ρ行的线，因此有很大概率当不同子群（以不同步长）进行行走时会走入同一个环。不同步长行走的点重合时，可以根据参数求解k，如式（3）所示。文献[3]给出了Pollard-rho算法过程。

由Pollard-rho算法的流程和算法思想可以发现：该算法的核心思想是在每次迭代中按照不同步长行走i步和2i步的点进行比较，二者相等时只要按照待定系数法即可求得k。算法第一步中选取子群的初始位置可以有多个，根据算法思想，初始位置变化后会对求解迭代次数有影响。从这个特征可以看出，Pollard-rho算法是一个随机型算法，无法给出其运算上界，只能给出其期望运算次数。综上所述，虽然Pollard-rho算法是ECDLP问题求解的有效算法，但是在计算资源无限的情况下仍然不能保证求出正确的解，而由于计算资源有限，求解ECDLP问题依旧被认为是困难的，由此保证了椭圆曲线加密体制的安全性[3]。

3 点乘优化算法和Pollard-rho算法仿真

协议攻击者根据监听消息破解用户私钥，从而求出最终密钥。通过求解该曲线上的ECDLP问题来完成目的，在k和n较小情况下模拟Pollard-rho算法的迭代求出迭代次数，并对曲线进行分析，根据复杂度估算Pollard-rho算法对于实际情况下的椭圆曲线的ECDLP问题破解时间。

数据导入处理和破解时间计算的平台为matlab，算法运行的平台为Visual Stdio 2010。

3.1 点乘优化算法仿真

对应的求逆元运算程序根据扩展欧几里得算法编写。这一方法分为求最大公因数和求模逆元两部分。该算法求模逆元的运算次数与辗转相除的次数m成正比，即时间复杂度为O(m)。由对应求模逆元程序运算次数为5m+5，计算量对比中运算次数取5m。在椭圆曲线密码体制计算中的数字乘法运算需加3次取模运算，平方运算需加2次取模运算。假定数字的乘法与取模运算计算次数为1，平方运算计算次数为3，乘法运算计算次数为4。以计算次数作为计算量单位，表2给出了部分仿真参数的具体数值，其中m为辗转相除次数。在椭圆曲线上点的坐标运算中，m随椭圆曲线参数中的p增大而增大，也受坐标差值而制约，因此处于波动状态，但有上界和下界。计算中，m取10。图2给出了密钥长度对点乘优化算法计算量的影响图。

表2 部分仿真参数和变量

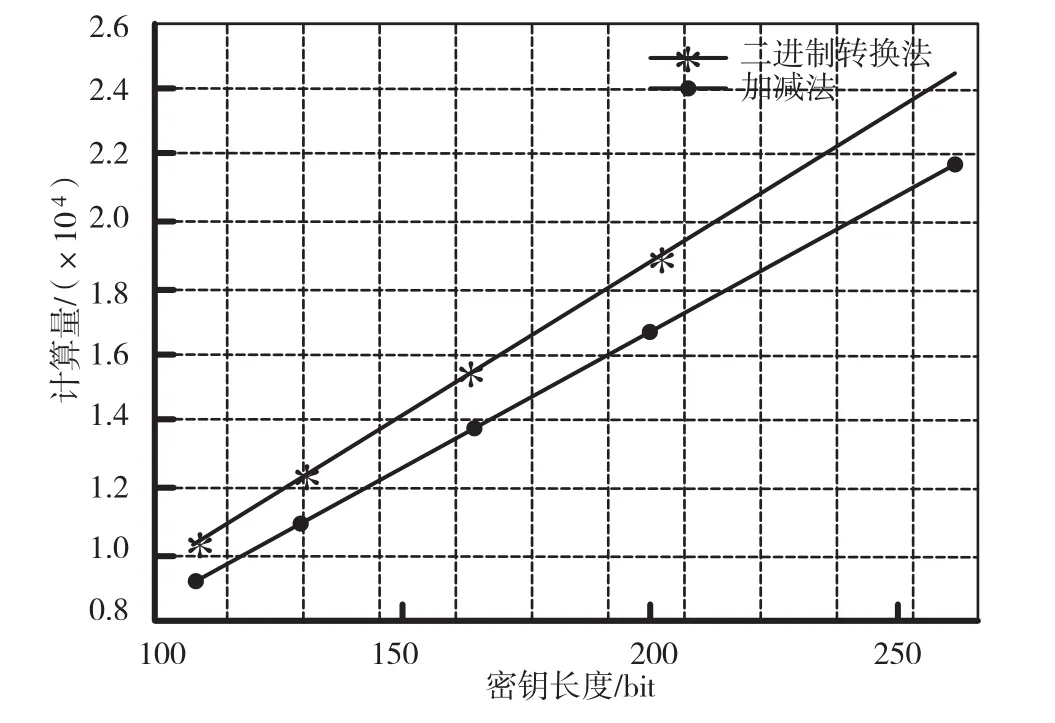
图2 不同密钥长度下两种算法性能比较

从图2看出，在不同密钥长度下，加减法的性能明显优于二进制转换法，同时加减法的计算次数与二进制转换法的计算次数成正比。但是，两种算法的计算量均比计算k次点加运算的计算量小很多。两种算法计算次数成正比的原因是，求逆元运算计算次数远大于乘法运算和平方运算。因此，两种算法的计算次数主要由二者求模逆元次数决定。

3.2 Pollard-rho算法仿真

3.2.1 阶数和密钥长短对Pollard-rho算法的影响

Pollard-rho算法是一个概率性算法，研究阶数和密钥大小对Pollard-rho算法求解ECDLP问题时迭代次数的影响。先在阶数n∈[20～211]、n取素数的前提下，对一定初始位置下Pollard-rho算法进行仿真对迭代次数进行统计。表3给出了部分仿真参数的具体数值。

表3 部分仿真参数和变量

图3为阶数n对算法迭代次数的影响曲线图。随着阶数n的增加，迭代次数总体呈折线式上升，其中该算法迭代次数与算法计算次数、时间复杂度成正比。这一结论验证了阶数n越大，求解ECDLP问题计算量越大，从侧面验证了椭圆曲线密码体制的安全性和协议可以抵抗监听者的被动攻击。

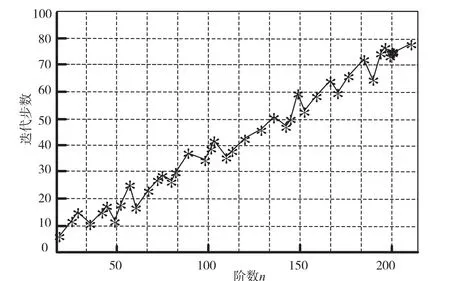
图3 阶数n对Pollard-rho算法迭代次数影响

密钥大小是随机生成的，小于椭圆曲线阶数的正整数。密钥不同，对Pollard-rho算法的迭代次数有着影响。在3个不同阶数的情况下，测试破解不同密钥需要的迭代次数。密钥大小取[2n-1]，n为阶数。表4给出了部分仿真参数的具体数值，图4给出了不同阶数的情况下不同密钥与需要的迭代次数关系图。

表4 部分仿真参数和变量

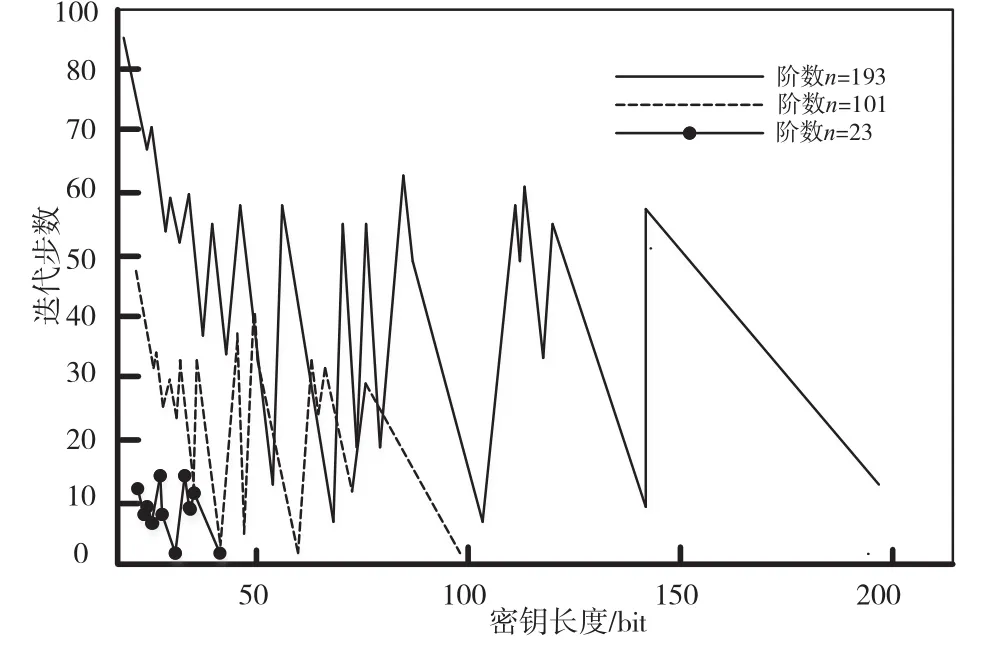
图4 密钥大小与Pollard-rho算法迭代次数关系

由图4的曲线可以得出以下结论：

（1）不同阶数的椭圆曲线密钥大小对Pollardrho算法迭代次数影响具有一定的相似性。3条曲线形状有很大的相似性，说明Pollard-rho算法具有一定的稳定性，无论对于阶数大小如何，所有大小的密钥破解情况具有相似性。

（2）对于一条既定椭圆曲线上的密钥，迭代次数随密钥大小递增有以下规律：k=2时取最大值，随后多次递增和递减，最后k接近阶数n时呈线性递减。

（3）得到曲线形状相似，验证了Pollard-rho属于概率性算法，一条曲线上破解密钥的平均迭代次数应与计算复杂度成正比。

根据结论两协议可以采取不安全密钥舍弃原则：产生的密钥过小或过大都不足够安全。密钥较小时，攻击者采用此算法迭代次数非常大，已知椭圆曲线参数的情况下，攻击者会先存储密钥较小时kp的坐标，若协议用户采用这种密钥，会直接被攻击者根据表内查找kp坐标，此时密钥安全性很低；密钥较大接近于阶数时，采用该算法迭代次数较低，密钥也不具有安全性。因此，协议用户在随机生成密钥后，若密钥符合上述两种情况，应当舍弃此密钥，选取适当大小的密钥，提高协议的可靠性。

3.2.2 密钥长度对破解时间的影响

随着密钥长度的增加，破解时间增加，对不同密钥长度下进行破解仿真。假设算法可实现求解，根据给出的算法复杂度，可估算破解时间。表5给出了部分仿真参数的具体数值。

表5 主要参数和变量

阶数n为合数，图5给出了密钥长度增加对破解时间的影响图。随着密钥长度增加，破解时间在对数坐标轴下呈线性增长趋势，即密钥长度增长时，破解难度增加，破解时间呈指数级上升。从图5可以看出，密钥长度为106 bit时，Pollard-rho算法的破解时间在104年量级；密钥长度为160 bit时，破解时间1012年量级。160 bit长度的密钥是安全的，对椭圆密码体制威胁很小。

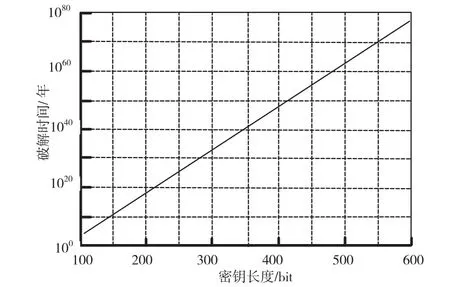
图5 密钥长度对Pollard-rho算法破解时间影响

4 结 语

通过对求解一般椭圆曲线上的ECDLP问题的Pollard-rho算法仿真，研究不同阶数和不同密钥对算法求解该问题的计算量影响，得出了随阶数增大，Pollard-rho算法计算量增大和不同阶数的椭圆曲线密钥大小对Pollard-rho算法迭代次数影响具有一定相似性的结论，并提出了一个针对协议的不安全密钥舍弃的原则。

根据Pollard-rho算法复杂度，估算出不同密钥长度下的破解时间，验证了椭圆曲线密码体制的安全性，证明了协议的可靠性，给出了协议应采用160 bit长度密钥的依据。