研经典图形 载数学文化——2019年杭州中考数学第21题赏析及教学启示

□姜佶楠

（杭州市采荷实验学校，浙江杭州 310020）

数学学习要以数学问题为载体，而几何问题离不开图形.杭州中考数学试卷中的几何问题，图形简约优美，表述简洁明晰，学生每道题都能上手，但如果想要得高分甚至满分，需要有扎实的基础知识和较强的解题能力.现以2019 年杭州中考数学第21 题为例，作粗浅评析，供批评指正.

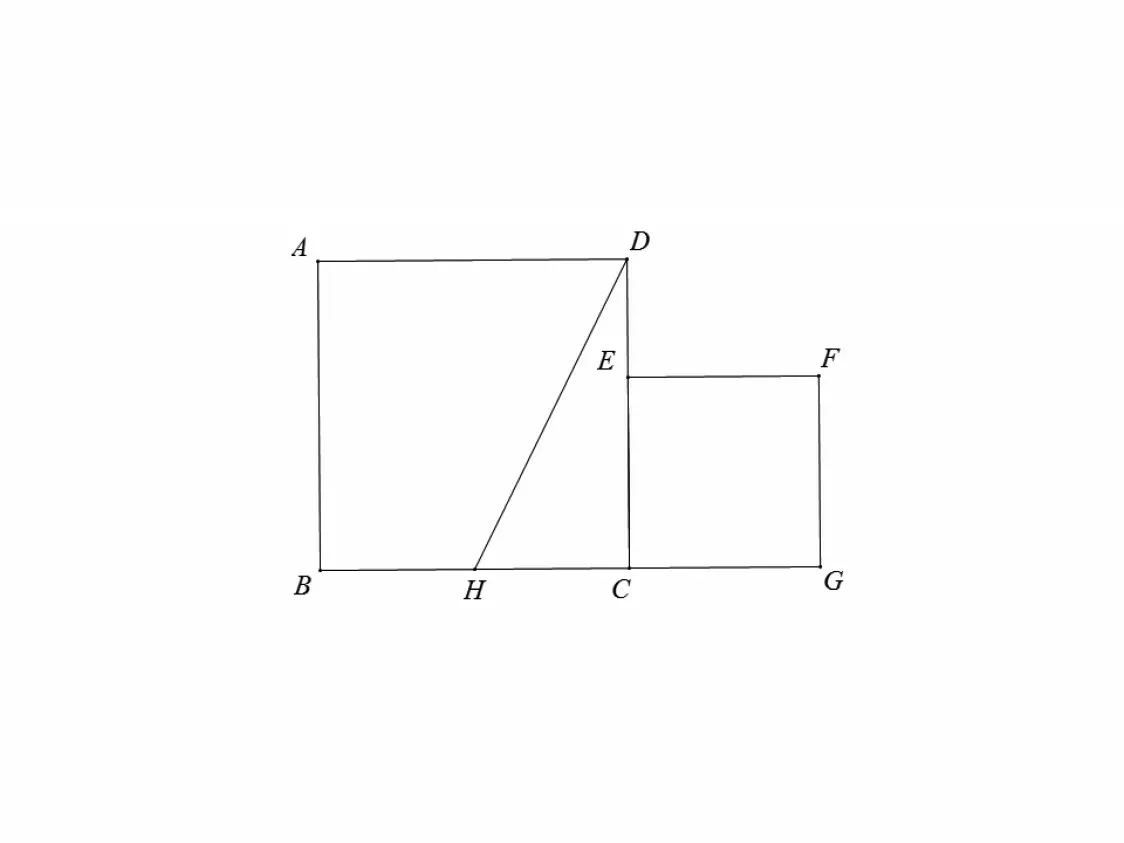
图1

试题如图1，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形面积为S2，且S1=S2.

（1）求线段CE的长；

（2）若点H为BC边的中点，连结HD，求证：HD=HG.

命题者秉承“回归课本，研究常见图形”的思路，选取了一个数学味十足的经典图形.问题设计指向明确，考查学生求线段长度的基本功，难度适中，能较好地检验学生对于通性通法的掌握情况.

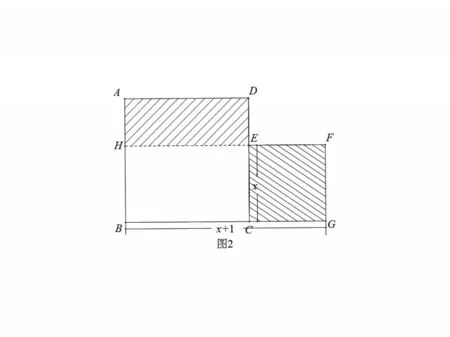
图2

一、优解题方法 现文化之源

关于第（1）问：

由面积相等建立方程，不妨设CE=x，则DE=1-x.

解 法1：如 图2，由S1=S2，即S矩形AHED=S正方形ECGF，

可得方程1（1-x）=x2，得

解法2：如图2，由S1=S2，可得S正方形ABCD=S矩形HBGF，

可得方程1=x（x+1），得

将面积相等转化为线段关系，还可以巧用黄金分割.

解法3：由S1=S2，即S矩形AHED=S正方形ECGF，

可得AD·DE=EC·EF，即

由正方形性质可得AD=DC，EF=EC，

且CD=1，因此

关于第（2）问：

∴HG=CH+CG=

∴HG=HD.

二、追图形之本 启文化之思

几何问题中，图形是“本”，是问题的“源”.试题本身并不复杂，对于大部分学生来说，也都能顺利解决，但对于教师来说，深入的后续思考，无疑是必要的.

本题的图形源自于《几何原本》第二卷的命题11，原命题是“可以切分已知线段，使它与一条小线段构成的矩形面积等于余下线段为边的正方形面积”.

欧几里得给出的方法如下：

以AB为边作正方形ABCD，取AD中点E，连结BE，延长EA至F，使EF=BE，以AF为边作正方形AFGH，延长GH交DC于点K.

则AB被H点所分，AB，BH构成的矩形面积等于以AH为边的正方形面积[1].

对于初中学生来说，这一结论通过计算，即可证明（如图3）.

设AE=a，可得图中各条线段长度，因此

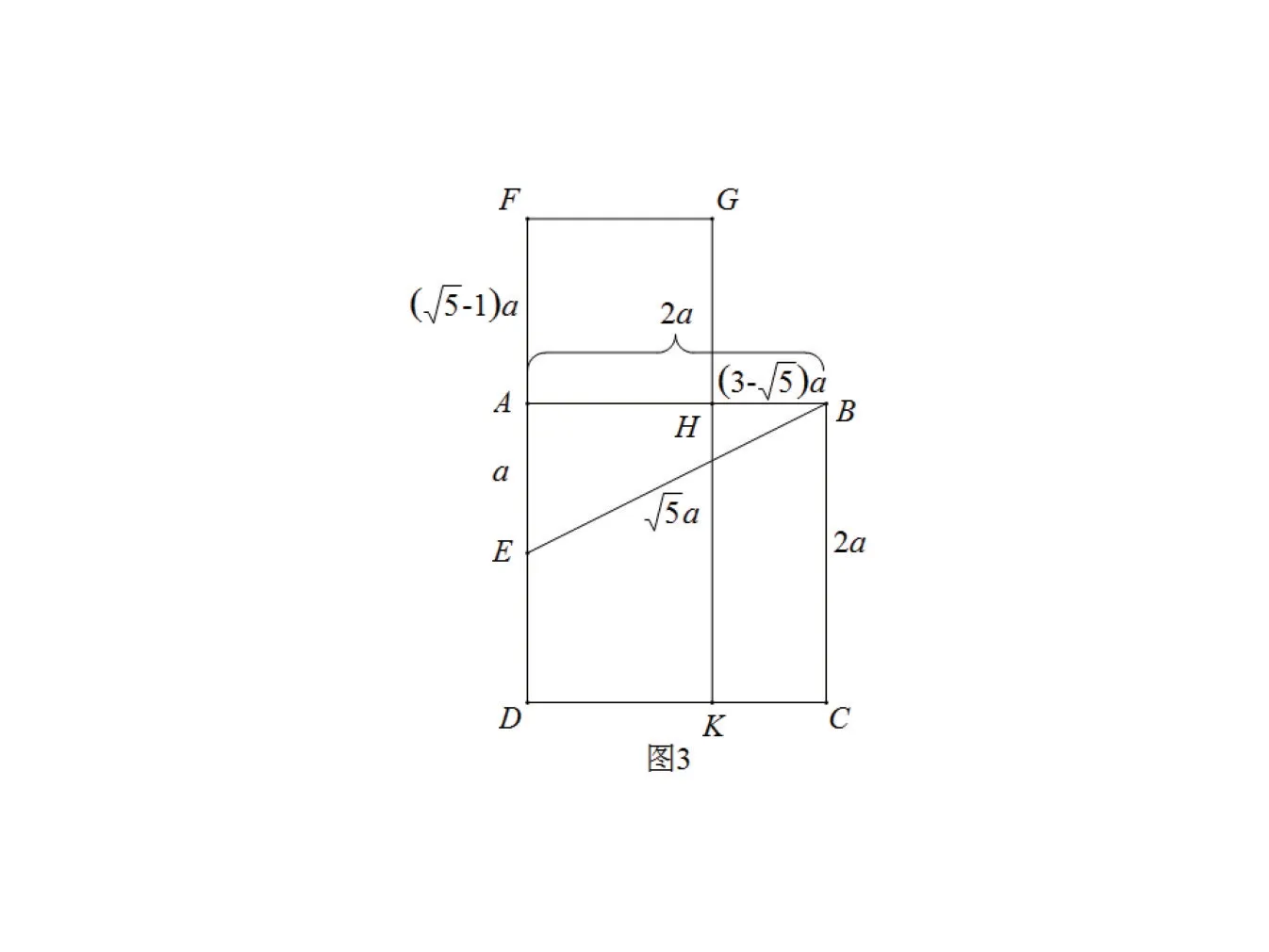
图3

可得S正方形AFGH=S矩形BHKC.

欧几里得在《原本》中给出的几何证法较为复杂，对于初中生来说，研究起来难度较大，此处不再赘述.近年的杭州中考几何问题，不止一次出现富有数学味的经典图形，如2018年的第21题，试题如下.

图4

如图4，在△ABC中，∠ACB=90°，以点B为圆心，BC的长为半径画弧，交线段AB于点D，以点A为圆心，AD长为半径画弧，交线段AC于点E，连结CD.

（1）若∠A=28°，求∠ACD的度数；

（2）设BC=a,AC=b.

①线段AD的长度是方程x2+2ax-b2=0的一个根吗？说明理由；

②若线段AD=EC，求的值.

此题源于浙教版八下第二章《一元二次方程》章末的阅读材料，是围绕《原本》中欧几里得给出的形如x2+ax=b2的方程的几何解法的经典图形，设计了求角度、线段，研究线段比例关系问题.

这两年杭州中考的第21题图形、知识点、方法不同，但共同特征是源于课本，取材于数学经典.简洁的图形和精练的题干可以让学生迅速抓住图形的特征，结合问题缩短思维链，找到解题方法，使每一名学生都能动手操作，尝试解题，充分体现了命题者对数学韵味和育人情怀的兼顾.

三、穷经典之用 重文化之基

（一）发展学生思维，满足不同需求

教学中可以将此图做进一步挖掘，发展学生的思维，通过多种方法的比较，满足不同思维水平学生的需要.如将原图下方的正方形截一半（如图5），设置以下三个问题.

已知：在矩形ABCD中，以点A为圆心，对角线AC的长为半径画弧，交射线AD于点E，以DE为边长作正方形DEFG，设AD=a，AB=b.

（1）线段DG的长度是方程x2+2ax-b2=0的一个根吗？说明理由；

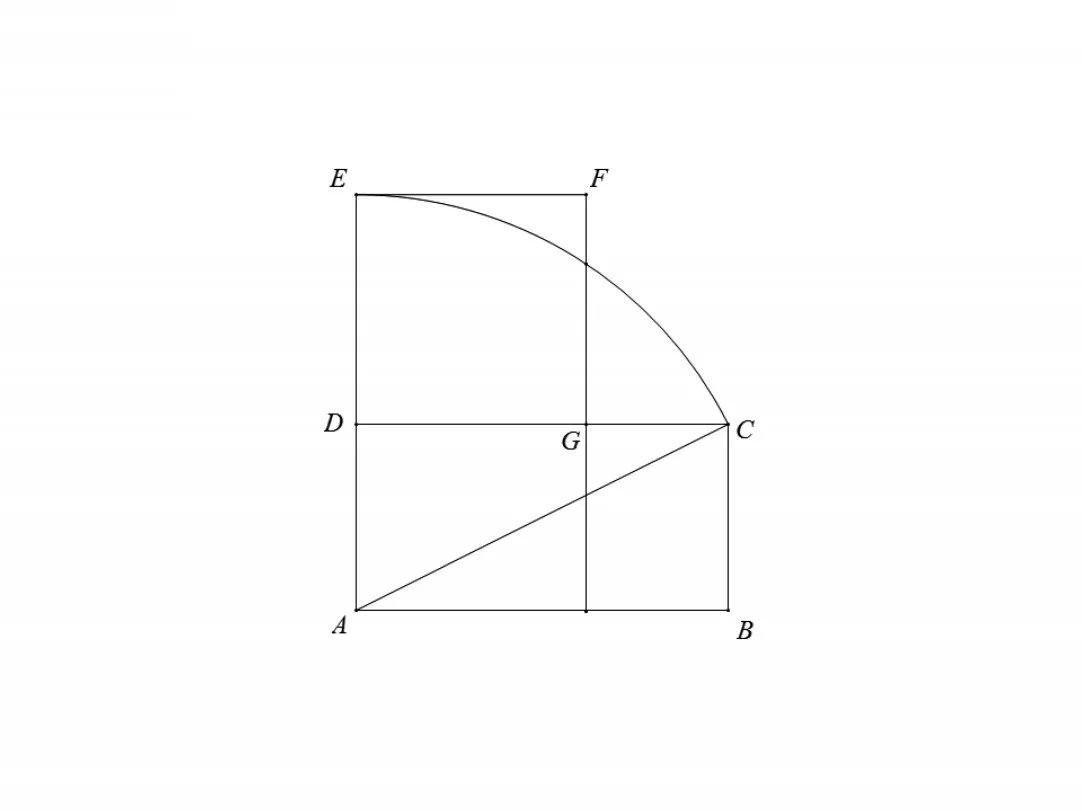
图5

（2）若点G是线段DC的黄金分割点（DG＞GC），求的值；

（3）在（2）的条件下，延长FG交AB于点H，探究S正方形EDGF与S矩形GHBC的数量关系.

考查的知识点依然是初中研究线段关系的常用方法，第（1）问直接应用勾股定理，设DG=x，在Rt△ACD中，AD2+CD2=AC2，

由题意：AC=AE，DE=DG，DC=AB，可得a2+b2=（x+a）2整理即得结论.

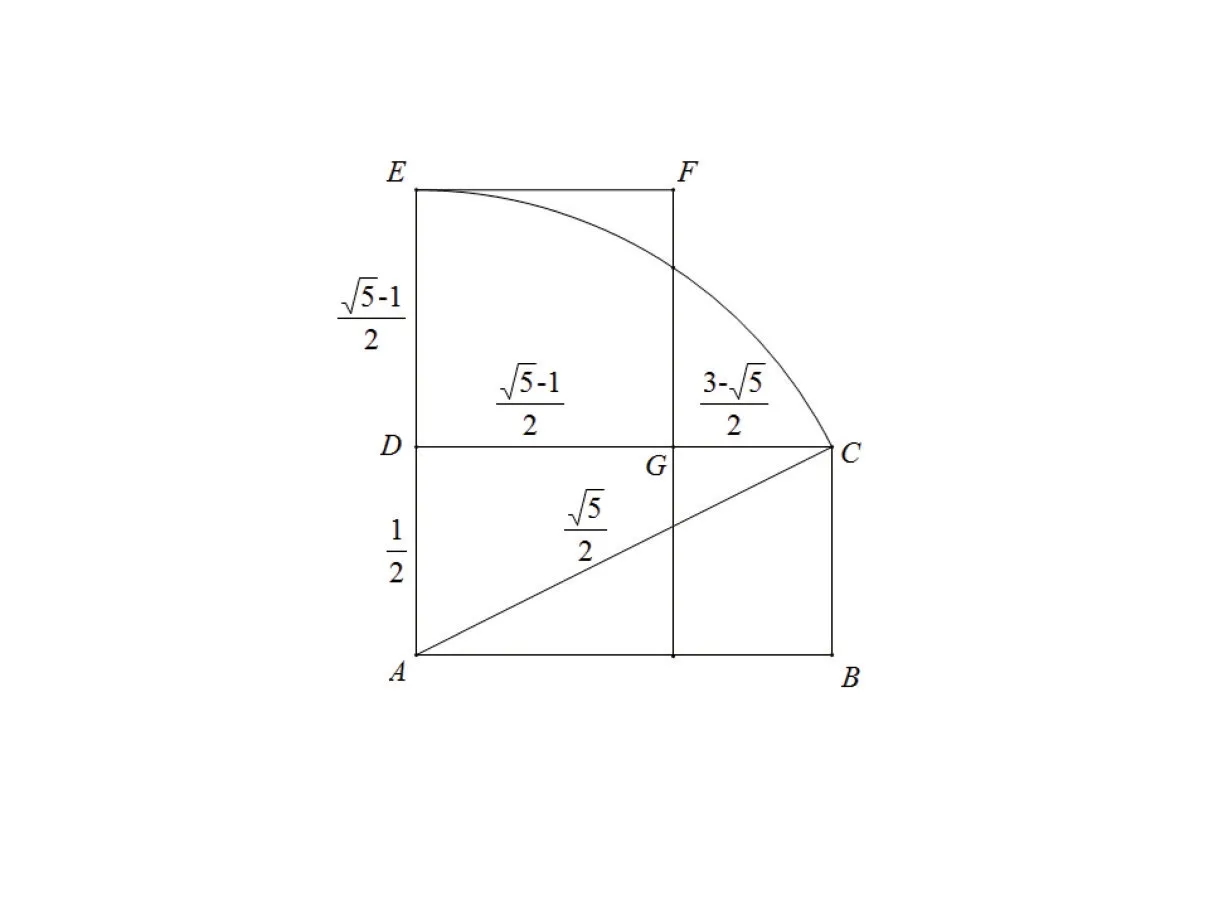
图6

第（2）（3）问 可 以 设DC=1，则DG=进而求得图中各线段长度（如图6），可得

继续计算S正方形EDGF

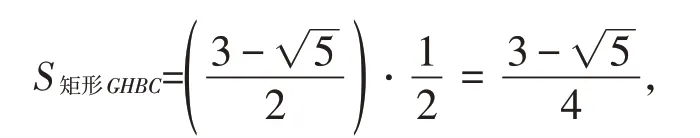
可得S正方形EDGF=2S矩形GHBC.

亦可利用黄金分割概念优化解法，由题意得DG2=DC·CG.

对于第（2）问，可设DG=x，则x2=b（b-x），整理得x2+bx-b2=0，结合（1）的结论x2+2ax-b2=0，可得

对于第（3）问，抓住黄金分割概念，S正方形EDGF=DG2=DC·CG，

又S矩形GHBC=CG·CB，由上题结论可知2BC=CD，可得S正方形EDGF=2S矩形GHBC.

通过五星酒店风机盘管控制方式及温控面板位置选择技术的探讨，全面罗列了目前主要的风机盘管控制方式，同时结合以往项目酒店案例设计情况进行综合分析，较为全面地总结了酒店各区域的风机盘管控制方式选择、温控面板的位置设置、数量以及外置温度传感器的设置，对于部分区域如公共卫生间及后场区域提出几种解决方案。

在解决第（1）问的过程中学生可能会将方程的根解出来，再代入图形中去验证，计算量较大.这一问的设计，主要是为了让学生通过解题，体会到虽然表面上涉及方程、代数式运算，但究其本质，还是研究图形中的线段关系.仅仅是运算的对象从具体的数变成了字母，运算的结果一般化、符号化，体会从特殊到一般，从具体到抽象的过程.

第（2）（3）两问，大部分学生采用了计算的方法，体现了大部分学生对于通性通法的掌握.第（2）问中，利用黄金分割的概念解决问题的学生较少，第（3）问由DG2联想到正方形面积的更是寥寥无几. 这启示我们，在新授课中，对于基本概念的教学，还有提升空间.对于思维水平较高的学生，这样的方法比较，有助于对概念的深入理解，助推高阶思维的发展.

（二）科学使用教材，强化知识联系

课本，是教学之本，我们要从“教教材”走向“用教材”，认真琢磨教材的设计意图.教什么？怎么教？教到什么程度？目标导向，充分挖掘教材资源的育人价值；分析学情，做好教材资源的校本化使用；深入研究，慎重而有依据地创新设计.在理解数学，理解学生，理解教学的基础上进行合理、充分地使用教材.例如，2018 年与2019 年的第21 题，都源于利用几何方法解决代数问题这一源头，对于这类问题，浙教版教材提供了许多有价值的资源.

浙教版八年级下册教师用书第50页，《第2章一元二次方程》章末小结“相关资源”：

如图7，在矩形ABCD中，AB=6，BC=11，P是边AD上一动点，（不含A，D），连结PC，E是AB上一点.

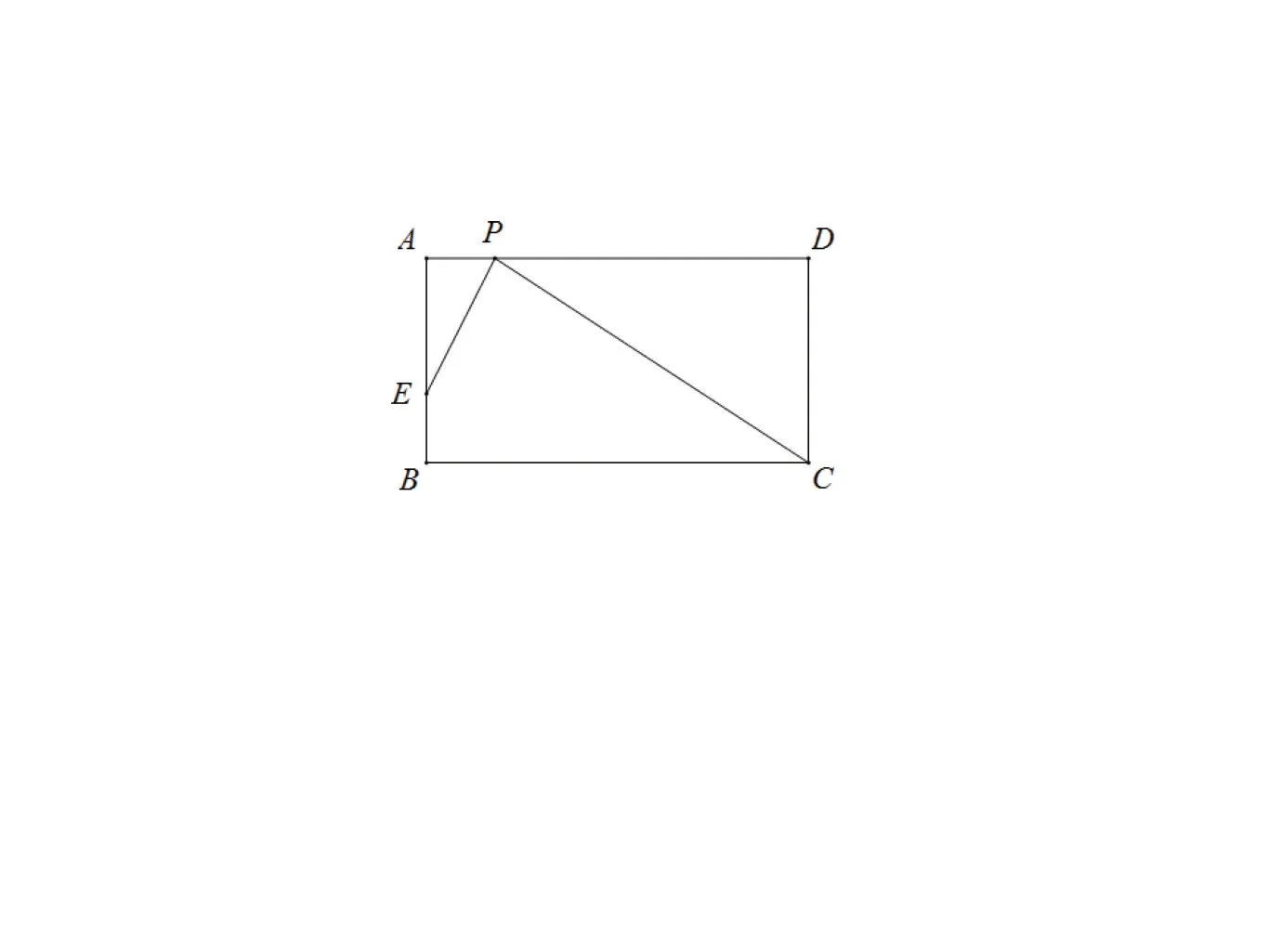
图7

（1）已知BE=2，是否存在点P，使∠EPC＝90°，若存在，求AP的长；若不存在，请说明理由；

（2）设BE=a，若存在点P使得∠EPC＝90°，求a的取值范围.

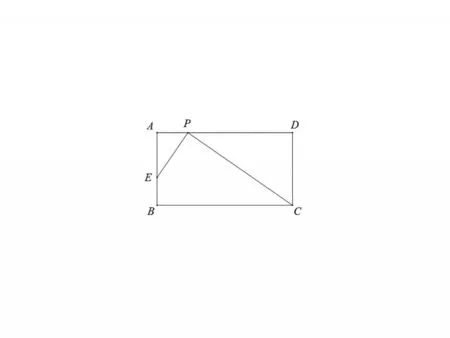
图8

教材提供这一资源的意图是强化学生利用二次方程解决实际问题时，需注意情境的存在性判定.但对于九年级学生来说，此题在中考复习中有着更大的价值，改编如下：

如图8，在矩形ABCD中，AB=6，BC=10，E在边AB上，BE=a，

P是边AD上一动点，连结PC，PE，若存在唯一的点P，使∠EPC＝90°，则a=___.

改变BC的长度是为了方便计算.

①从代数角度思考：不妨设AP=x，易由

△APE∽△PDC得即

整理得x2-10x+36-6a=0，

从方程角度理解，可利用Δ=0 求出a的值；

从函数的角度，可变形为a关于x的二次函数利用二次函数性质求得最值并检验是否可行.

②从几何角度看，可知P点轨迹为以CE中点O为圆心，OE长度为半径的半圆上，由题意得，要使得P点唯一存在，则圆与边AD相切（如图9），连结OP并反向延长，交BC边于点Q.

图9

教材和学生，是我们教学最重要的资源，如果能与学生一起，挖深、讲透这样的例题，对于学生形成知识之间的横向联系，发展以数释形、以形助数的逻辑闭环，是有所裨益的.

由此可见，只有深入理解数学，理解课标，才能充分挖掘教材资源，谨慎而有创造性地使用教材资源，让学生通过解题，经历过程，积累经验，感悟方法.

（三）融入数学历史，重视学习体验

近年来，包括杭州在内的许多省市的中考卷中，出现了源于或者改编自数学历史的经典问题的考题.因此，开发数学史，助力日常教学，是素养立意的教育改革的大势所趋，也是充分发挥数学育人价值的必然要求.

1.体现人文价值，激发学习兴趣

例如，在给出无理数的定义之前，可以尝试在课堂上探讨根号的由来，将无理数历史加以介绍，让学生了解这一数学符号及数学历史的发生、发展过程，是数学人文价值的体现；的几何意义，更体现了“数学文化”的核心，它不仅充分展示了数学知识发生、发展及应用的过程，更包含“数形结合”等思想方法，也实现了从“一维”到“二维”的思维方式的跨越.

2.重构发生过程，加深概念理解

在给出无理数定义时，也可以结合“有理数可以用两个整数之比来表示”这一特征，凸显无理数与有理数的区别及无理数存在的必要性，在此基础上给出定义——不能用两个整数之比表示，再根据有理数的小数表征、无理数的小数表征，加深学生对无理数的概念和表征的理解，也体现了知识的发生、发展过程.

美国数学史家卡约黎的研究表明，学生所遭遇的困难往往是相关学科的创建者经过长期思索和探讨后所克服的实际困难，为了让学生深刻理解数学概念，教师有必要从数学发展历史的角度进行课堂设计，帮助学生突破认知障碍.

3.丰富学习体验，感受数学魅力

回溯无理数的发展历史，学生会意识到，数学知识也是随着时间不断发展变化的，这一过程也并非一帆风顺.在2000 多年漫长的历史中，数学家们对于无理数这一概念的不断探索和研究，也培养着学生的理性精神和批判思维，让学生亲近数学，感受数学的魅力[2].