平面向量概念教学的诊断与改进
2019-12-04白改平徐元根褚海峰
□白改平 徐元根 褚海峰
(1.浙江师范大学教师教育学院,浙江金华 321004;浙江师范大学行知学院,浙江金华 321004)
一、向量概念的教学地位和教学争议
向量是高中数学的核心概念,不仅丰富了数学内容,扩充了运算体系,而且作为一种工具,简化几何证明,成为沟通代数、几何和三角的桥梁.很多教师认为后者是高中向量教学的重点,而向量概念的教学并不那么重要[1].为此,在实际教学中,一线教师基本按照教材的编排,通过向量的物理背景引入概念,然后以菜单的形式把概念一个个讲清楚.那么,这种教学方式究竟合不合适?要回答这个问题需要考虑以下三个问题.
(1)数学中的向量和物理中的矢量是否完全一致?
向量包括固定向量和自由向量两种.自由向量只考虑向量的大小和方向,而起点的位置是任意的;但固定向量除了向量的方向、大小确定外,起点的位置也是确定的.数学中所研究的向量是自由向量,正是由于向量的起点可以根据实际问题的需要自由移动,才使得运用向量解决问题具有方便性、简洁性.而物理中的矢量(如作用力)许多情况下需要考虑作用点的位置.可见物理中的矢量和数学中的向量还是有差异的,所以如果按照教材的编排实施教学,从物理背景中抽象出向量概念的本质特征,这并不利于学生真正理解数学中的向量.
(2)学生是否对向量的本质有较好的认知?学习向量的认知基础和障碍是什么?
向量的本质是什么?为什么研究平行向量?向量平行和直线平行有什么差异?零向量的方向是任意的,那么零向量唯一吗?如何理解零向量和任意向量平行?向量可以比较大小吗?为什么?对于这些问题,学生事实上是迷惑的.由此看来,向量概念的教学并不容易.
(3)向量概念的教学目标是什么?如何培养学生的数学核心素养?
本节课是一节概念课,从其地位和学生的认知深度来看,显然不是一节“似乎没什么东西可讲,也没什么难点”[2]的课.目前,培养学生的核心素养是数学教学的终极目标,数学概念承载着培养数学抽象素养和数学建模素养的主要任务,而作为核心概念的向量对于实现上述任务义不容辞,所以向量概念的教学并不是简单地教授其形式化定义及几个相关概念就可以了.
二、向量概念的教学诊断与分析
本节课的主要特征是概念繁多,但每个定义的字面意义浅显易懂,没有什么隐晦或难以理解的关键词.事实上,越简单的课越难教.本节课的重心在于如何在繁多的概念中根据学生已有的认知基础设计一些具有矛盾冲突的问题,由表及里,层层深入,突破障碍,帮助学生真正领会向量的本质.
(一)运用概念形成的模式,体验学习向量的必要性
概念形成和概念同化是学习数学概念的两种方式,它们的学习过程有本质差异.概念同化依靠的是新旧知识的联系,而概念形成依靠的是对具体事物的抽象概括.两种方式没有优劣之分,只是适用的对象和目的不同.概念同化适用于发展性概念,其作用在于以旧知识为生长点,通过比较、分类帮助学生认识新概念,形成概念体系.而概念形成适用于起始概念和原始概念,其作用在于帮助学生理解概念的本质,体会概念产生的背景和发展学生数学抽象的核心素养.向量对学生而言是一个全新的概念,需要学生对认知结构进行重组和改造,而且从培养学生核心素养的角度来看,概念教学尤其是核心概念要尽可能体现概念的形成过程,让学生参与概念本质特征的概括活动,所以本节课的学习适合概念形成.
(二)遵循数学概念形成模式,创设合适情境,抽象向量概念
概念形成是从大量的具体实例中抽象出一类事物的本质属性,并用符号加以表示.其一般过程是“观察分析具体例子—归纳概括共同特征—抽象出本质属性并给出定义—用符号表示”,这就是学生认识一个新概念的基本思路,也是培养学生数学抽象的核心素养的主要策略.
本节课的教学理应遵循概念形成的步骤,通过具体实例的创设,引导学生从这些模型中归纳概括出向量概念的本质属性.力、位移、速度、加速度等原型确实为向量概念提供了直观的、具体的、现实的背景,但是由于数学中的向量是自由向量,为了突出这一特征,教师需要对物理背景进行加工和改造,或者另起炉灶创设合适的向量模型.
(三)运用学生认知基础,为学生概括和领会向量概念搭建合理有效的脚手架
向量的本质特征是大小和方向,这两个要素对高中生而言并不陌生.在学生已有的认知中,方向是刻画位置及其关系的量,如直线的平行或共线等;而长度是刻画形如数量、数量间的大小关系、长度、面积、体积的量,这为学生自觉、有序、有效地认识本节课的相关概念提供了“生长点”.基于以上事实,教学时可以类比数的概念的抽象过程揭示向量概念的本质属性,类比直线的位置关系认识向量的基本关系.
三、几个有争议的教学环节及改进策略
根据以上分析,数学教师不仅在认知上需要重新认识向量概念的教学地位,更需要在教学行为上努力创新,突破教材的编排,设计高效的教学.
(一)导入环节:创设合适的情境,抽象概念
导入语:生活中,数学无处不在.黄河,波澜壮阔,底蕴深厚.李白曾赞叹道:“君不见,黄河之水天上来,奔流到海不复回.”
情境:假设水流速度是匀速的,在不考虑风速等的理想状态下,5片落叶同时掉入河流中.经过一分钟后,它们的运动轨迹如图1所示.
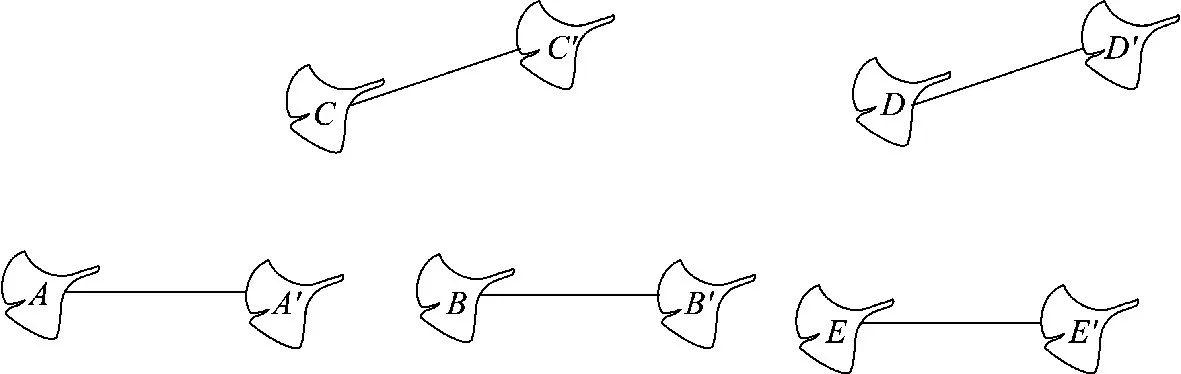
图1
问题1:如何表示这5 片树叶的运动状态?
师生活动:学生尝试用自己的方式表示这5 片树叶的运动轨迹.通过比较分析,引导学生用有向线段表示(如图2).
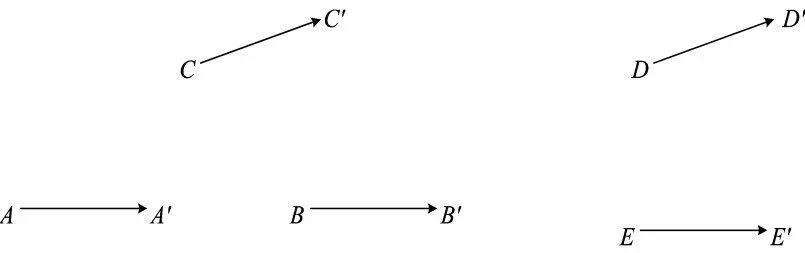
图2
【设计意图】概念抽象需要典型丰富的具体事例.创设这样的问题情境,可以培养学生用数学的眼光认识世界,而且让学生感受到向量概念不是凭空产生的.
问题2:对图中的5条有向线段如何分类?分类的标准是什么?
【设计意图】数学思想方法是数学知识更好层次的抽象概括,是数学的精髓,是培养数学核心素养的主要手段.分类的过程不仅有助于提升学生的思维能力,而且确立分类标准的过程就是对向量本质属性大小和方向抽象的过程.
问题3:仔细观察这两组有向线段,除了具有大小和方向之外还有什么特征?
师生活动:教师通过几何画板的动态演示让学生发现:有向线段BB',EE'通过平移和AA'重合,有向线段CC'通过平移和DD'重合.
【设计意图】对学生而言,向量起点的任意性是认识的障碍或者是认识的盲区,为此设计5个起点不同的向量模型,通过动画演示帮助学生建立向量可以自由移动的事实,从而有效地揭示了自由向量的本质,并为相等向量奠定基础.
(二)发展数学抽象的核心素养环节:类比自然数,领会数学抽象的真谛
问题1:既有大小又有方向的量叫向量.这样的例子有很多,同学们还能够举出生活和学习中关于向量的一些例子吗?并思考数学中的向量和物理中的矢量有什么异同.
师生活动:按照学生已有的经验,学生会举出形如力、速度、位移、加速度等矢量,师生共同逐一分析它们之间的联系和差别.
【设计意图】通过比较物理中的矢量和数学中的向量的异同,打破学生已有的认知,明确数学中向量起点是任意的,只要方向和大小确定,向量就唯一确定,从而真正领会向量的本质特征.
问题2:谁能描述一下向量概念的抽象过程?
教师引导:刚才从落叶的移动这一现实背景中抽象出了向量的概念.抽象是数学的一种基本思想,也是用数学眼光观察世界的体现.比如:数字3 的认识,最初是从3 根手指,3 个苹果,3 把椅子等开始,然后从这些具体事例中抽象出它们的共同属性——这些集合的元素个数相等,用数字3表示,这里的3既不是3根手指,也不是3个苹果.再来看向量的概念,有向线段虽然起点不同,但是具有相同的大小和方向,我们将这两个共同属性抽象出来,就形成了向量的概念.同样,这里的向量既不是有向线段也不是有向线段
【设计意图】数学的抽象性要求概念教学的最终目标是让学生获得数学研究对象、认识数学新对象的基本方法,学会用数学的方法刻画和研究现实生活的方法和途径.通过回忆向量的抽象过程,让学生明白认识数学概念的基本方法和思路,同时帮助学生建立类和集合的数学思想方法.
问题3:在数学中,学习了概念的定义之后,就要思考如何表示?
【设计意图】通过向量的表示,揭示向量具有代数形式和几何形式的“双重身份”,让学生明确只用代数或几何形式表示向量是不够的,必须两者结合.
(三)合理分类,明确向量间的关系
问题1:向量满足两个要素:大小和方向,那么两个向量有什么关系?有几种情况?请完成表1.
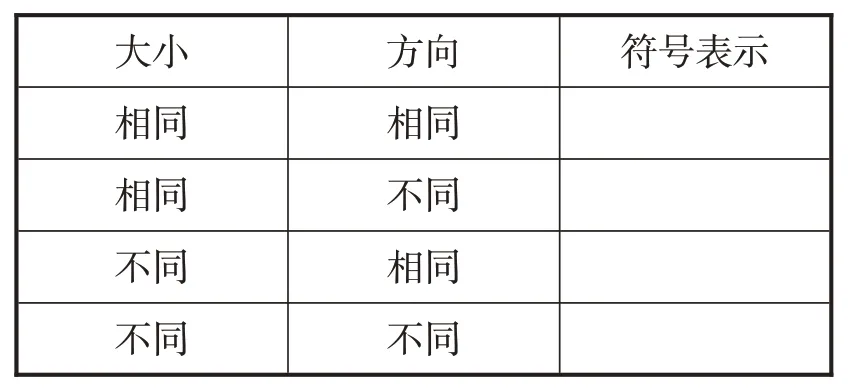
表1
【设计意图】这节课概念繁多,如果一个概念接一个概念地讲,很容易引起学生思维的懈怠,也会造成知识之间支离破碎.而通过分类,学生必须经过火热的思考,思维得以发展,概念间的体系也顺利建立.
问题2:向量的平行、共线与线段的平行、共线有什么联系与区别?
【设计意图】让学生把向量概念和几何知识联系起来,在比较中认识共性,明确差异,最终构建良好的知识体系.
问题3:把一组大小相同、方向不同的向量平移到同一起点,它们的终点形成了什么图形?
师生活动:师生共同发现大小相同、方向不同的向量构成一个非常美的图形——圆,从而引出模的概念,记作|AB|.
【设计意图】人教版教材首先介绍的是向量的模和向量的表示,然后再介绍相等向量、相反向量、平行(共线)向量,在这里却是通过对向量的分类先认识了向量间的关系,再引出向量的模.这样改编的好处是紧紧围绕向量的两个要素,在分类的过程中认识相关概念,使得概念的引出水到渠成.
问题4:模是数量还是向量?在自然数中有两个特殊的量是0 和1,数学中把模等于1的向量叫单位向量,把模等于0 的向量叫零向量.
问题5:类比自然数0 和1,思考为什么把单位向量和零向量称为特殊向量.
【设计意图】自然数0有三大功能:是正负数的分界点;有了0 就可以定义相反数;加强了自然数的运算功能.自然数1的主要功能是计数单位.通过回忆自然数0和1的作用,能自然而然类比出单位向量和零向量的作用,这为后续学习向量的运算和向量的坐标表示奠定基础.
数学概念是数学内容的最小单位,是学习数学知识的基石,是思维的细胞,是判断、推理的起点,是培养数学能力的前提.所以数学概念教学的核心不仅在于使学生掌握书本知识,更重要的是让他们经历数学概念的形成历程和概括过程,领悟数学家用数学的观点看待和认识世界的思想真谛,进而提高提出问题、分析问题、解决问题的能力.
