激光闪射法测量金属试样导热系数的不确定度评定的探讨

王 洛,刘自民,饶 磊,樊明宇,王俊北,冯顺华

(马鞍山钢铁股份有限公司技术中心 安徽马鞍山 243002)

导热系数的检测方法众多，有热流法、保护热板法、热线法和激光闪射法[1]等，其中激光闪射法因其原理简单、测量范围大且测量速度快捷而得到广泛研究和应用。[2]-[5]

由于测量误差的存在，对被测量值的不能肯定的程度由不确定度表示[6]。一般不确定度愈小，表明结果与被测量的真值愈接近，质量越高，可信赖程度越高。目前，大部分日常检测项目已有较成熟的不确定度评定方法，但激光闪射法测量材料的导热系数的不确定度评定仍比较少见[7]。因此，针对金属试样导热系数的不确定度评定开展相关工作具有重要的实际意义。

1 激光闪射法测试原理说明

激光闪射法通过直接测量材料的热扩散系数计算导热系数，其基本原理如图1所示：首先，炉体控制一定的温度，然后由激光源发射的光脉冲均匀照射在待测样品(圆柱：1 mm-6 mm厚，20 mm或12.5 mm直径)的下表面，使试样均匀加热，通过红外检测器连续测量得到样品背面温度(检测器信号)随时间变化的函数。再由Fourier传热方程公式(2)便可得到试样的热扩散系数。通过比较法测得待测样品的比热值，同时结合待测样品的热扩散系数和体积密度，按照公式(1)计算测得试样的导热系数。

λ(T)=α(T)×CP(T)×ρ(T)

(1)

(2)

式中：λ(T)为温度T下样品的导热系数，w/(m·K)；α(T)为温度T下样品的热扩散系数，cm2/s；Cp(T)为温度T下样品的比热容，J/(g·K)；ρ(T)为温度T下样品的密度，g/cm3；h为样品的厚度，mm；t50为半升温时间，s。

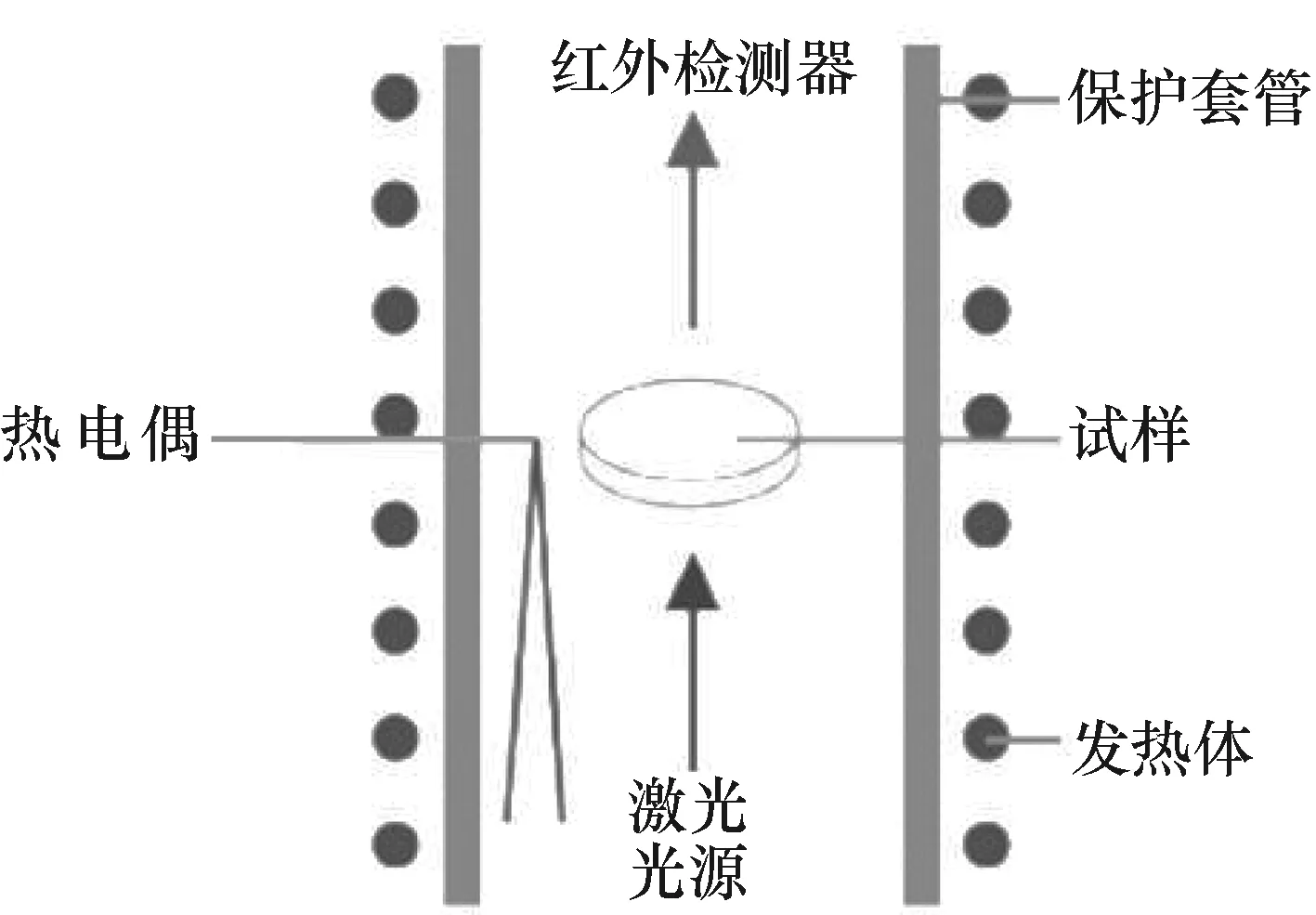
图1 激光闪射法测试原理示意图

2 激光闪射法测试导热系数试验说明及计算模型

本工作使用的设备是德国耐驰仪器制造有限公司的LFA427型激光闪射导热仪。首先，将金属试样制备为直径为Ø12.5 mm，质量为2.64 g的圆柱形圆片，上下两表面平行且光滑，试样的厚度应由试样的热扩散系数所定，用游标卡尺实测厚度为2.56 mm，在200 ℃进行10次测量，10次测量结果如表1所示。

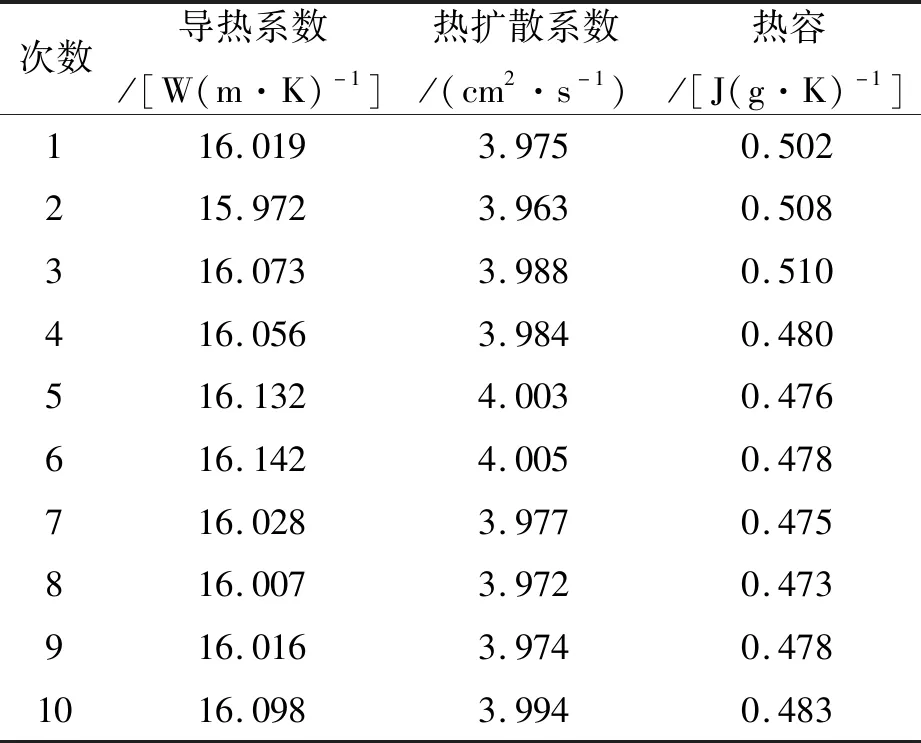
表1 激光闪射导热仪测量结果

在检测过程中，待测样品的密度通常在室温下测量，其随温度升高的变化可使用材料的热膨胀系数进行修正，在测量温度不太高、样品尺寸变化不太大的情况下，也可近似认为不变。体积密度的测量标准有量尺法和浸水法。对于金属试样来说，试样的平行度、平整度较好，且采用量尺法较为方便，因此按式(3)计算不确定度。

(3)

3 不确定度的来源

激光闪射法测量导热系数的不确定度来源较多，根据(3)式分析主要的来源有质量m、厚度h、底面直径d、温度T等。

3.1 厚度测量的不确定度

3.1.1 厚度重复性测量引入的不确定度(A类)

在常温下对待测试样厚度进行10次测量，所得结果如表2所示。

表2 常温下测量10次所得试样厚度数据

根据贝塞克公式可得标准偏差为：

=0.016mm

取四个值来作为最终的输入结果，所以厚度重复性测量的标准不确定度为：

3.1.2 测量样品厚度引入的计量不确定度(B类)

根据游标卡尺的检定证书，当置信水平为95%，k=2时，测量不确定度为0.01 mm，所以，由游标卡尺测量样品厚度引入的不确定度为：

综上，由厚度引入的标准不确定度为：

=0.008mm

相对标准不确定度为：

3.2 底面直径引入的不确定度

3.2.1 直径重复性测量引入的不确定度(A类)

在常温下对待测试样底面直径进行10次测量，所得结果见表3所示。

表3 常温下测量10次所得试样底面直径数据

根据贝塞克公式可得标准偏差为：

=0.048mm

取四个值作为最终的输入结果，直径重复性测量的标准不确定度为：

3.2.2 测量样品直径引入的计量不确定度(B类)

根据游标卡尺的检定证书，当置信水平为95%，k=2时，测量不确定度为0.01 mm，所以，由游标卡尺测量样品直径引入的不确定度为：

综上，由直径引入的标准不确定度为：

=0.025mm

相对标准不确定度为：

3.3 t50测量引入的不确定度

3.3.1t50重复性测量引入的不确定度(A类)

在常温下对同一样片进行10次测量，由于实际测量中试样厚度为输入的常数，根据(2)式可计算出t50，所得结果如表4所示。

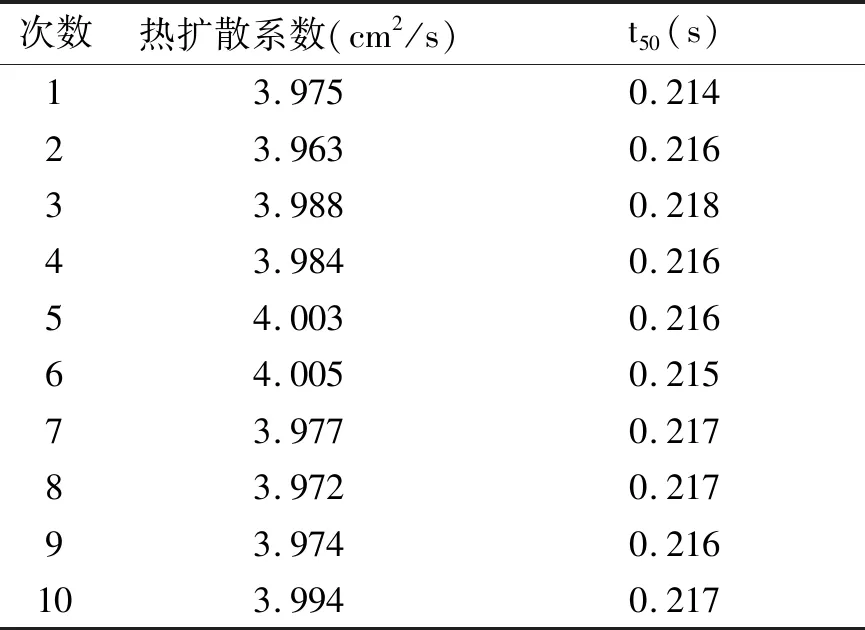
表4 常温下测量10次所得热扩散系数和t50数据

根据贝塞克公式可得标准偏差为：

=0.0012s

所以t50重复测量的标准不确定度为：

3.3.2t50的计量不确定度(B类)

由于仪器时间最小计量单位为0.001 s，假设为均匀分布，由此引入的标准不确定度为：

综上，由半升温时间测量的标准不确定度为：

=0.0013s

相对标准不确定度为：

3.4 热容测量引入的不确定度(B类)

由德国耐驰提供的热容测试的准确率为±5%，按照正态分布来考虑不确定度，其置信概率为99.73%，可知引入的相对标准不确定度为：

3.5 质量测量引入的不确定度(B类)

由电子天平检定证书提供的电子天平的扩展不确定度为0.11 mg，k=2，可知引入的标准不确定度为：

相对标准不确定度为

3.6 温度引入的不确定度(B类)

热电偶检定证书显示为2级，偏差为±0.25%T，视其为均匀分布，引入的相对标准不确定度为：

3.7 合成标准不确定度

将上述的相对标准不确定度标准进行合成，试样的导热系数λ的标准不确定度为：

=16.05×1.82%=0.28W/(m·K)

3.8 扩展不确定度

在本次评定中，包含因子k=2，扩展不确定度为：

U(λ)=2u(λ)=0.58W/(m·K)

3.9 结果报告

在室温200 ℃下以量尺法测量Ø12.5 mm×2.56 mm的金属试样的体积密度时，测试结果的不确定度为U(λ)=0.58W/(m·K)，最终测试结果为：λ=(16.05±0.58)W/(m·K)。不确定度分量结果汇总如表5所示。

表5 各不确定度分量汇总表

4 影响因素分析

从上文数据分析过程可以看出：

热容测量所引入的不确定度显著，由此表明对比法是测试试样导热的重要误差来源。根据设备厂家提供的资料，通过比较法测试试样的比热容误差通常为±5%。通过表1可知，本次测量所得比热容的标准偏差为1.4%，而各测试结果与平均值的相对误差最高可以达到4.94%，因此，对于待测试样的导热系数结果要求较高时，建议尽量增加测试时闪射点的个数，而对于需要精确测量导热系数的金属试样，其比热容结果须用DSC分析仪进行测量。

半升温时间(半升温时间t50表示待测样品背面接受激光照射后温度升高到最大值的一半所需要的时间)引入的不确定度同样显著。由此表明，除了设备自身重复性，系统的计量性能与校准也是误差的重要来源，建议定期对设备进行标样的比对试验。

5 结论

在室温200℃下以量尺法测量Ø12.5 mm×2.56 mm的待测金属试样的体积密度时，测试结果的不确定度为U(λ)=0.58W/(m·K)，最终测试结果为：λ=(16.05±0.58)W/(m·K)。

对于激光闪射法测量金属试样导热系数过程，试样的比热容是影响其结果的最主要因素。因此，对于待测试样的导热系数要求较高时，建议尽量增加同一温度闪射点的个数，而在需要精确测量金属的导热系数(<3%)时，试样的热容须用DSC进行测量。

对于激光法测量金属试样导热系数的过程，除了设备自身的重复性，系统的计量性能与校准也是误差的重要来源。