谈谈函数与导数的复习(上)
2019-12-02许少华
许少华

函数与导数是永恒的高考热点,看看2019年全国(1)卷数学题,其中,客观性试题4道20分,主观性试题一道12分,共32分.这五道题中高、中、低档一应俱全、应有尽有.再看看全国(2)卷、(3)卷及其它省市的试卷,那一份不是如此?可以说,函数与导数是全国范围内任何一位考生都无法逃避的内容,要想真正在高考中取得好成绩,这一内容必须过关. 那么我们在进行高考复习时,从哪些方面入手就有可能获得较为理想的效果呢?本文和你慢慢聊一下.
一、图像类问题
面对函数的解析式,从已知图像中选出与已知函数较为相符的图像是此类试题的重要特征,请看:
例1 (1)函数f(x)=■的图像大致是( )
(2)函数y=■在[-6, 6]的图像大致为( )
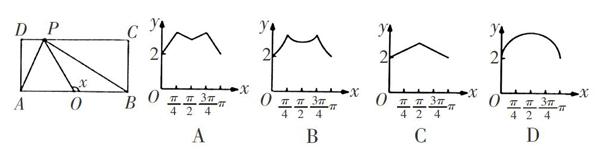
(3)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x. 将动点P到A,B两点距离之和表示为x的函数f(x),则f(x)的图像大致为( )
解析 (1)B.该函数为奇函数,奇函数关于原点对称,故排除选项A中的图像;当x>0时,ex-e-x,f(x) > 0,故排除选项D中的图像;取特殊值,当x=1时,e-■>2,而不接近函数值1,故排除选项C中的图像.
(2)B. 由y= f(x) = ■在[-6, 6],知f(-x) = ■=■=-f(x),
∴ f(x)是[-6, 6]上的奇函数,因此排除C;又f(4)=■>7,因此排除A,D.
(3)B. 由已知得,当点P在BC边上运动时,即0≤x≤■时,PA+PB=■+tanx;当点P在CD边上运动时,即■≤x≤■,x≠■时, PA+PB=■+■,当x=■时,PA+PB=2■;当点P在AD边上运动时,即■≤x≤?仔 时,PA+PB=■-tanx,从点P的运动过程可以看出,轨迹关于直线x=■对称,且f(■)>f(■),且轨迹非线型,故选B.
点评 建立在解析式的基础上寻找图像问题,往往较为灵活,处理方法:由粗变细. 往往先看奇偶性,然后,再看图像中的特殊点、单调性等,在看单调性时,不排除利用导数.本例中的第(3)题,难度明显要大一点,它必须要求先产生解析式,再寻找图像.
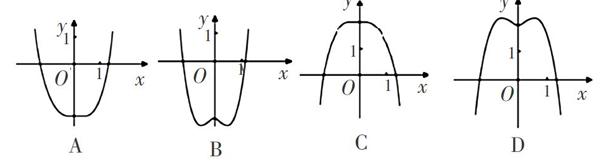
跟踪练习1.(1)函数y=-x4+x2+2的图像大致为( )
(2)函数y=2x2-e|x| 在[-2, 2]的图像大致为( )
答案 (1)D. 当x=0时,y=2,可以排除A、B选项;又因为y′=-4x3+2x=-4x(x+■)(x-■),则 f′(x)>0的解集为(-∞, -■)∪(0, ■),f(x) 单调递增区间为(-∞, -■),(0, ■);f′(x)<0的解集为(-■, 0)∪(■, +∞),f(x)单调递减区间为(-■, 0),(■, +∞). 结合图像,可知D选项正确.
(2)B. f(2)=8-e2=8-2.82>0,排除A;f(2)=8-e2<8-2.72<1,排除B;
当x>0时,f(x)=2x2-ex,f′(x)=4x-ex,当x∈(0, ■)时,
f′(x) <■×4-e0=0.
因此,f(x)在(0, ■) 单调递减,排除C,故选D.
二、函数性质类问题
结合函数性质设计试题随处可见,这些题的结合点与联系点往往较为丰富,试题形式也多彩多样.
例2 (1)已知f(x)是定义域为(-∞, +∞)的奇函数,满足f(1-x)=f(1+x). 若f(1)=2,则f(1) + f(2) + f(3) + …+f(50)=
( )
A. -50 B. 0 C. 2 D. 50
(2)已知函數f(x)(x∈R)满足f(-x)=2-f(x),若函数y=■与y=f(x)图像的交点为(x1, y1), (x2, y2),…,(xm, ym),则■(xi , yi)=( )
A. 0 B. m C. 2m D. 4m
(3)设函数f(x)=■(a<0)的定义域为D,若所有点(s, f(t)) (s, t∈D)构成一个正方形区域,则a的值为
( )
A. -2 B. -4 C. -8 D. 不能确定
解析 (1)C. 因为函数f(x)为定义域R上的奇函数,f(1-x) =f(1+x),所以f(0)=0,T=4,由题意可知:f(4)=f(2)=f(0)=0,f(3) =-f(1)=-2,所以f(1)+f(2)+f(3)+f(4)=0所以2≡50mod4,所以f(1)+f(2)+f(3) + … + f(50)=f(1)+f(2)=2+0=2.
(2)B. 由f(x)=2-f(x)得f(x)关于(0, 1)对称,而y=■=1+■ 也关于(0, 1)对称,∴对于每一组对称点xi+xi′=0,yi+yi′=2,∴ ■(xi +yi)=■xi +■yi =0+2·■=m.
(3)B. 由 |x1-x2|=fmax(x),■=■,|a|=2■,a=-4.
点评 这三道题很精干、很优美,它们的联系也很广泛,可以看出,这类试题没有基本模式、没有规范,随机性很大,因此,想让它难度有多大,完全在命题操作之中.
跟踪练习2.(1)函数y=■的图像与函数y=2sin ?仔x,(-2≤x≤4)的图像所有交点的横坐标之和等于( )
A. 2 B. 4 C. 6 D. 8
(2)设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0, 1]时,f(x)=x(x-1). 若对任意x∈(-∞, m],都有f(x)> -■,则m的取值范围是( )
A. (-∞, ■] B. (-∞, ■] C. (-∞, ■] D. (-∞, ■]
答案 (1)D. 函数y=■的对称中心是(1, 0),同时也是y=2sin ?仔x(-2≤x≤4)的中心,-2≤x≤4他们的图像在x=1的左侧有4个交点,则x=1右侧必有4个交点. 不妨把他们的横坐标由小到大设为x1,x2,x3,x4,x5,x6,x7,x8,则x1+x8=x2+x7=x3+x6=x4+x5=2,故选D .
(2)B. 由f(x+1)=2f(x)及x∈(0, 1]时,f(x)=x(x-1)∈[-■, 0]可知,当x<0时,f(x)>-■恒成立.
当x∈(1, 2]时,f(x)=2(x-1)(x-2)∈[-■, 0],此时f(x)> -■恒成立.
当x∈(2, 3]时,f(x)=4(x-2)(x-3)∈[-1, 0],此时由4(x-2)(x-3)=-■得x=■或x=■,于是m≤■.
三、大小比較问题
大小比较问题一直都存在于各级各类考试的试卷之中,而这是一类容易被人们忽视之题,其实,大小比较对基本函数性质的考查力度相当大,它应用的隐藏性与灵活性也是其它试题难以比拟的.
例3 (1)设x,y,z为正数,且2x=3y=5z,则( )
A. 2x<3y<5z B. 5z<2x<3y C. 3y<5z<2x D. 3y<2x<5z
(2)若a>b>1,0 A. ac 解析 (1)取对数:x ln 2= y ln 3= z ln 5. ■=■>■,∴ 2x>3y,x ln 2= z ln 5,则■=■<■,∴ 2x<5z,∴ 3y<2x<5z,故选D. (2)C. 由于0 要比较a log b c和b log a c,只需比较■和■,只需比较■和■,只需b ln b 和a ln a. 构造函数f(x)=x ln x (x>1),则f′(x)=ln x+1>1>0,f(x)在(1, +∞)上单调递增,因此f(a)>f(b)>0?圳a ln a>b ln b>0?圳■<■,又由0 ∴ ■<■?圳 a log b c 要比较log a c和log b c,只需比较■和■,而函数y= lnx 在(1, +∞)上单调递增,故a>b>1?圳ln a>ln b>0?圳■<■. 又由0 点评 可以看出大小比较并非一定是基础题或简单题,有的难度明显较大. 对于本例中的第(2)题也可以取特殊值,比如令a=3,b=2,c=■直接代入分析,过程会简单很多. 跟踪练习3.(1)设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则( ) A. f(log 3 ■)>f(2■)>f(2■) B. f(log 3 ■)>f(2■)>f(2■) C. f(2■)>f(2■)>f(log 3 ■) D. f(2■)>f(2■)>f(log 3 ■) (2)设a=log 0.2 0.3,b=log 2 0.3,则( ) A. a+b (3)设a=log 3 6,b=log 5 10,c=log 7 14,则( ) A. c>b>a B. b>c>a C. a>c>b D. a>b>c 答案 (1)C. 因为f(x)是偶函数,所以 f(log 3 ■)= f(log 3 4),因为2■<2■<1 (2)B. ∵ a= log 0.2 0.3,b= log 2 0.3,∴ ■= log 0.3 0.2,■= log 0.3 2, ∴ ■+■=log 0.3 0.4,∴ 0<■+■<1即0<■<1. 又∵ a>0,b<0,∴ ab (3)D. 根据公式变形,a=■=1+■,b=■=1+■,c=■=1+■. 因为lg 7>lg 5>lg 3,所以■<■<■,即c 四、借助导数处理函数性质问题 在客观性试题中设计导数在函数中的应用问题非常常见,此类题往往难度较大,无论是试题结构还是试题类型都很漂亮,值得研究与欣赏. 例4 (1)若函数f(x)=(cos x-sin x)(cos x+sin x)+3a(sin x -cos x)+(2a+1)x 在上(-■, 0)单调递增,则a的取值范围为( ) A. [-1, ■] B. [-1, ■] C. [-1, ■] D. [-■, 1] (2)设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0,使得f(x0)<0,则a的取值范围是( ) A. [-■, 1) B. [-■, ■) C. [■, ■) D. [■, 1) (3)已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围为( ) A. (2, +∞) B. (-∞, -2) C. (1, +∞) D. (-∞, -1) 解析 (1)D. 由于f′(x)=-2sin2x+3a(cos x+sin x)+2a+1. =-2(cos x+sin x)2+3a(cos x+sin x)+2a+3≥0恒成立. 由于cos x+sin x=■sin(x+■),因为x∈(-■, 0),得-1 ≤cos x+sin x≤1. 令g(t)=-2t+3at+2a+3(-1≤ t ≤1),欲使g(t)≥0恒成立,只需g(-1)≥0,g(1)≥0,即-2(-1)2+3a×(-1)+2a+3≥0,-2+3a+2a+3≥0?圯-5≤a≤1. (2)设g(x)=ex(2x-1),y=ax-a,由题意,存在唯一的整数x0,使得g(x0)在直线y=ax-a的下方. 因为g′(x)=ex(2x+1),所以当x<-■时,g′(x)<0,当x>-■时,g′(x)>0,所以当x=-■时, [g(x)]min=-2e■,当x=0时,g(0)=-1,g(1)=e>0,直线y=ax-a恒过(1, 0)斜率且a,故-a>g(0)=-1,且g(-1)=-3e-1>-a-a,解得■≤a<1,故选D. (3)由已知a≠0,f(x)=ax3-3x2+1有唯一的正零点,等价于a=3·■-■有唯一的正零根. 令t=■,则问题又等价于a=-t3+3t有唯一的正零根,即y=a与y=-t3+3t有唯一的交点且交点在在y轴右侧记f(t)=-t3+3t,f′(t)=-3t2+3. 由f′(t)=0,t= ±1,t∈(-∞, -1),f′(t)<0;t∈(-1, 1),f′(t)>0;t∈(1, +∞),f′(t)<0,要使a=-t3+3t有唯一的正零根,只需a 选B. 点评 做一做这些“小题”,确实会感觉这些试题的构造相当巧妙,不一定很难,但每一道题都十分灵活、从分析到求解都有可圈可点之处,都是不可多得的好题. 跟踪练习4. (1)已知函数f(x)=ln x+x2+x. 正实数x1, x2满足f(x1)+f(x2)+x1x2=0,則下述结论中正确的一项是( ) A. x1+x2≥■ B. x1+x2<■ C. x1+x2≥■ D. x1+x2<■ (2)已知平行于x轴的直线分别交两曲线y=e2x+1与y=■于A,B,则 |AB| 的最小值为( ) A. ■ B. ■ C. ■ D. ■ (3)若函数f(x)=(x2-ax+a)ex-x2(a∈R)在x=0处取得极小值,则a的范围为( ) A. a≥1 B. a>0 C. a<0 D. a≤0 答案 (1)A. 设g(x)=x-ln x (x>0),g′(x)=1-■=■, 易知g(x)在(0, 1)上单调递减,在(1, +∞)上单调递增,故g(x)min =f(1)=1. 由f(x1)+f(x2)+x1x2=0得ln x1 +x1 2+ln x2+x2 2+x1+x2=0, ∴ (x1+x2)2+(x1+x2)=x1x2-ln(x1x2). 由于g(x)≥1,从而x1x2-ln(x1x2)≥1, ∴ (x1+x2)2+(x1+x2)≥1,解得x1+x2≥■. (2)A. 由■?圯x1=■(ln a-1),而x2满足a=■?圯x2=■(a2+1), |AB|=x2-x1=■(a2+1)-■(ln a-1). 令f(a)=■(a2+1)-■(ln a-1)?圯f′(a)=■= ■. 易得当a=■时,|AB|min =f(■)=■. (3). 由f′(x)= xex(x+2-■-a),令f′(x)=0得x=0或x+2-■-a=0. 令g(x)=x+2-■即x=0或g(x)=a. 由于g(x)在(-∞, +∞)上单调递增,且值域为R,故存在唯一零点x0,使得g(x0)=0. ①若x0>0,则x∈(-∞, 0)时,g(x) < a,此时,f′(x)>0;当x∈(0, x0)时,g(x) < a,此时,f′(x)<0. 因此,f(x)在x=0处取得极大值,与题意不符. ②若x0=0,f(x)在x=0处不取极值,与题意不符. ③若x0<0,则x∈(x0, 0)时,g(x) > a,此时,f′(x)<0;当x∈(0, +∞)时,g(x) > a,此时,f′(x)>0. 因此,f(x)在x=0处取得极小值. 综上,知x0<0,于是a=g(x0) 故a的范围为a<0,选C. 责任编辑 徐国坚
