高职院校英语A级考试成绩预测模型的构建

韩海云， 李苑辉， 吴 晗

(三亚航空旅游职业学院 a.国际旅游学院； b.人文社科学院，海南 三亚 572000)

高等学校英语应用能力考试(简称PRETCO)[1]于2000年正式实施，发展至今，已为全国20余省、市、自治区采用，是衡量高职高专学生英语水平的标准考试。本门考试主要考核学生用英语进行日常和职场交际的能力，旨在促进高职高专英语教学向培养高等应用技术型人才的转变；同时为用人单位提供评价高职高专毕业生英语水平的标准，以提高学生进入职场的竞争力。高等学校英语应用能力考试分A,B两级，A级考试为高职高专学生应该达到的标准要求。

目前，英语A级考试已经成为衡量高职高专英语教师教学效果与学生英语水平的“标杆”。对教师而言，A级考试在促进教师教学、改进教学方法、丰富教学内容、理解和执行教学大纲、培养学生英语综合运用能力等方面都有明显的作用。大学英语也含有提高学生应用英语能力的部分，也能够在一定程度上反映学生的英语能力。因此，学生平时的英语课程成绩与其A级考试成绩应当是高度相关的。因此，可以假设：在 A级考试之前，基于学生在校英语课程成绩是可以预测出其在A级考试中可能取得的成绩。预测A级成绩作用体现在：一方面，教师可通过对考试成绩的预测分析整体上把握学生对知识的掌握程度；另一方面，可帮助教师较为准确地估计每位学生的学习状态，进而对预测成绩较低的学生提出预警，并针对性地调整教学方法和教学模式。

目前有不少学者通过构建各种模型对考试成绩进行预测，多采用贝叶斯分类模型预测[2]、决策树算法[3]、遗传神经网络模型[4]、随机森林模型[5]、多元线性回归模型[6-7]、灰色理论预测[8]及其萤火虫优化神经网络[9]对已收集的成绩数据进行预测分析，且经过验证，模型预测的准确性比较高。因此，这些模型的预测结果可以对相关学科的教学起到很好的指导作用。然而，从现有的文献看，对A级考试成绩进行预测的研究几乎没有。本文拟通过收集部分学生的成绩数据，尝试构建一套英语A级考试成绩的预测模型，并检验该预测模型的准确性，为高职院校英语A级考试成绩预测与评价提供借鉴。

一、 数据来源与建模过程

(一)数据来源

本研究从三亚航空旅游职业学院教务系统数据库中提取机电工程学院2017 级机电设备维修专业的3个班级共106位专科生第一学期成绩报表中的英语成绩，包含平时成绩、卷面成绩、高考成绩以及首次A级考试成绩，如表1所示。样本学生首次参加英语A级考试是入学的第一学期期末(2017年12月)，此时其已修完大学英语(一)。因此系统中已形成建模所需数据。

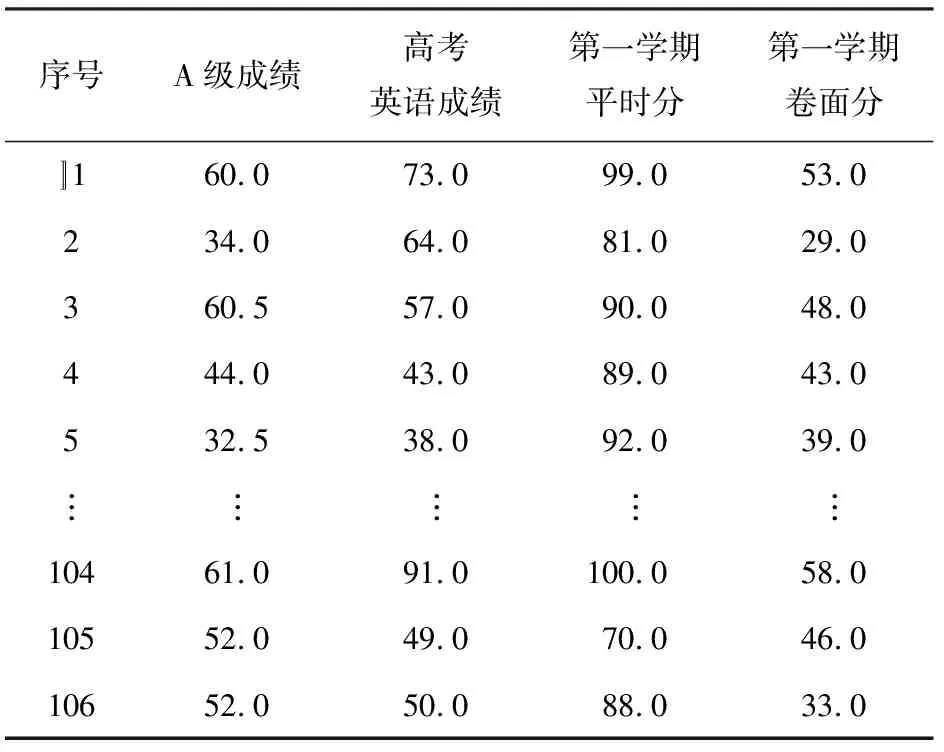
表1 样本学生的英语相关成绩数据提取 /分

(二) 模型构建步骤

1．选择因变量

本研究的目标是预测A级考试成绩，因此选择样本中的A级成绩为因变量。

2． 确定自变量对因变量的解释力

分别作出A级成绩与高考英语成绩、第一学期平时成绩、第一学期卷面成绩的散点图，如图1-3所示。从图中可以看出，A级成绩与3个变量均无明显的线性依存关系，因此不适合用一元线性回归方程进行拟合。现尝试引入多元线性回归。

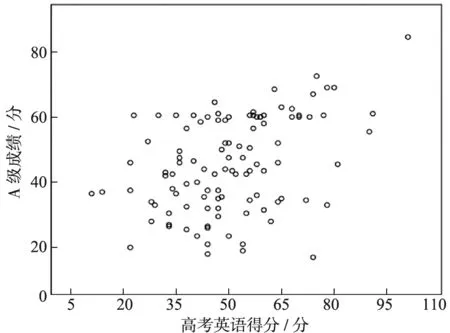
图1 A级成绩与高考英语得分散点图

图2 A级成绩与第一学期平时成绩散点图

图3 A级成绩与第一学期卷面成绩散点图

多元线性回归需满足以下五个条件，缺一不可[10]：

(1)线性是合理的，因变量与自变量之间只存在线性关系，不存在非线性关系；

(2)随机误差零均值，互相独立，且方差相等；

(3)随机误差具有相同的分布，都服从正态分布；

(4)随机误差与自变量相互独立；

(5)自变量之间互不相关。

现用SPSS 软件，将高考英语成绩、第一学期平时成绩、第一学期期末成绩3个自变量代入多元线性回归模型，显示结果如表2-4所示。

表2 线性回归模型的各参数汇总

注：a表示预测变量(常量),包括第一学期卷面成绩、第一学期平时成绩、高考英语得分。

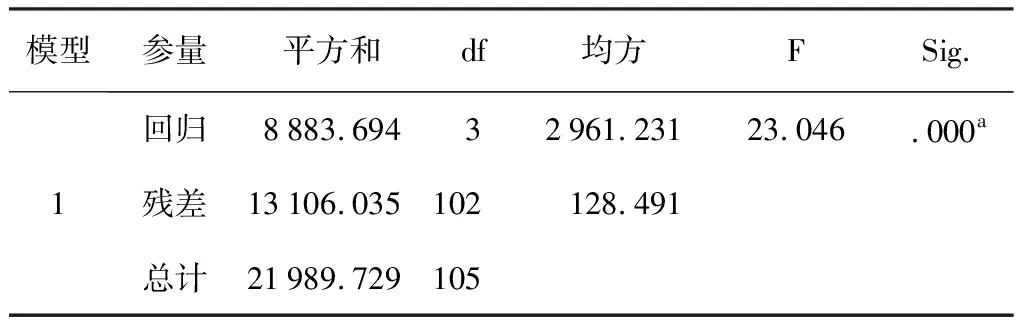
表3 方差分析

注：a表示预测变量(常量),包括第一学期卷面成绩、第一学期平时成绩、高考英语得分。

表4 回归系数表

从表3可以看出，方程的显著性检验能够通过，回归系数不全为0；但是，表4中，假定显著性水平为0.05，则“第一学期平时成绩”“第一学期卷面成绩”两个变量的回归系数显著不为0，其余变量的回归系数不显著。出现这种状况的原因在于多元线性回归中自变量之间存在多重共线性。

3． 消除自变量的多重相关性

多重共线性是指变量之间存在较强的线性相关性，破坏了多元线性回归的第5个条件：自变量不相关。现采用逐步回归方法让SPSS自动选择合适的自变量用于建立回归方程，与已选变量发生多重共线性的变量会被剔除出回归模型，从而得到一个多重共线性较小的线性拟合方程。表5为消除多重共线性后的结果。

从表5所示的拟合优度可以看出，第二个模型比第一个模型有了提高，表明第二个模型优于第一个模型。接着看表6方程的显著性检验结果。

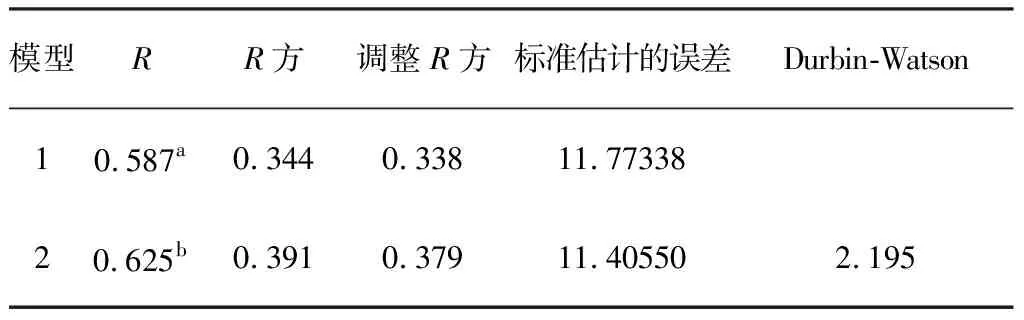
表5 两个线性回归模型的各参数汇总

注：a表示预测变量(常量),包括第一学期卷面成绩、高考英语成绩；b表示预测变量(常量),包括第一学期卷面成绩、第一学期平时成绩。

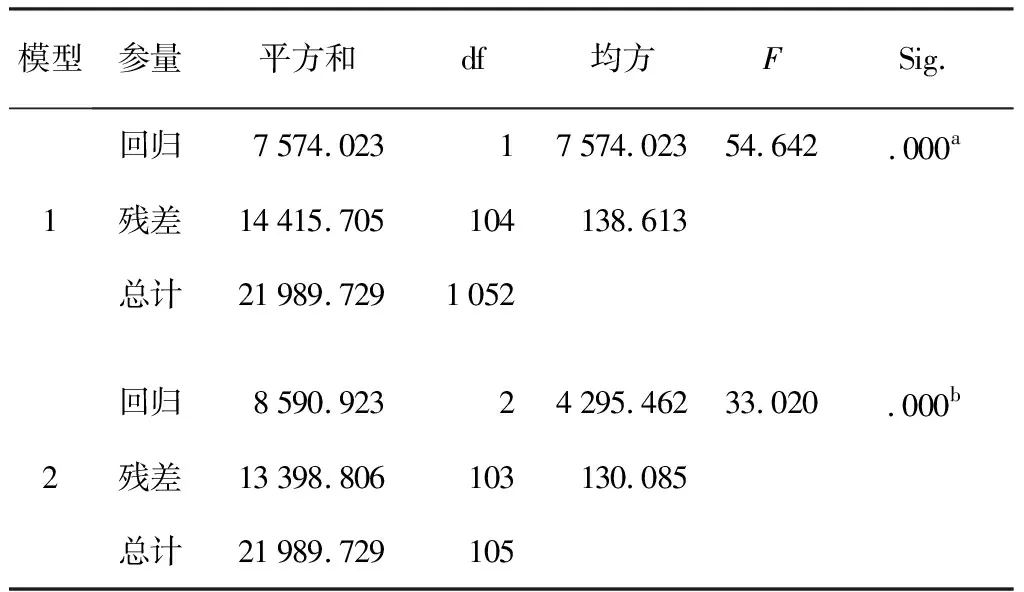
表6 两个模型的方差分析

注：a表示预测变量(常量),包括第一学期卷面成绩；b表示预测变量(常量),包括第一学期卷面成绩、第一学期平时成绩。

从表6可以看出，两个模型都通过了方程显著性检验，说明两个模型的回归系数都显著性不为0.表7是系数显著性检验结果。

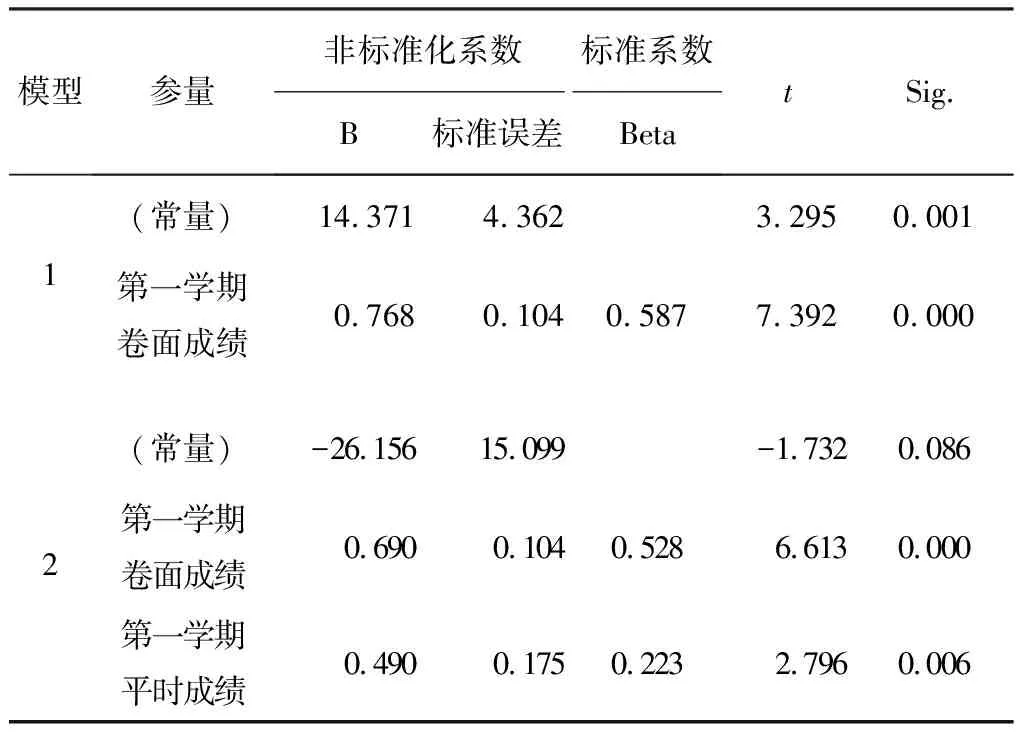
表7 两个模型的回归系数表

从表7可看出，两个模型的系数都是显著的，第二个模型比第一个模型增加了第一学期平时成绩变量，拟合优度显著增加，因此应该增加该变量。

4． 拟合线性回归方程

综上所述，可得A级成绩的多元线性回归拟合方程：

5． 检验方程

式中的回归系数表示卷面成绩每提高10分，A级成绩有望提高6.9分；平时成绩每提高10分，A级成绩有望提高4.9分。

6． 分析残差

(1)作出正态P-P图，如图4所示。

(2)从图4可以看出，残差数据基本服从正态分布。接下来通过Durbin-Watson统计量对残差进行自相关分析。Durbin-Watson统计量的值为：(ei-ei-1)的平方和除以ei的平方和。

Durbin-Watson统计量取值在0～4之间。当残差正相关时，即ei，ei-1接近，则Durbin-Watson统计量取值接近于0.同理，当残差负相关时，即ei，-ei-1接近，则Durbin-Watson统计量取值接近于4.Durbin-Watson统计量取值接近于2时，说明随机误差不存在自相关。

图4 残差的累积概率对比

7． 确认模型

从表5可以看出，Durbin-Watson统计量取值为2.195，接近于2，说明序列不存在自相关。因此可确认A级成绩的预测模型为：

二、 模型应用

现将3个班共30个测试样本数据按照此多元线性回归模型进行预测，即将测试样本的的大学英语课程平时成绩和期末成绩代入模型，得到其本次A级考试的预测值，然后该样本学生参加同一场全国大学英语应用能力A级考试。在全国统考分数下发之后，将模型的预测成绩与A级全国统考的实际成绩进行对比，结果显示25位学生的预测值与实际的A级成绩误差在5分以内，准确率达到了83.3%，如表8所示。采用同专业其他班级英语课程的数据进行测试，准确率也达到了80%以上，说明此预测模型是有效的。通过对学生成绩的预测分析，我们可以看到，平时成绩差的学生成绩预测分数和实际分数基本为不及格；卷面成绩较好(50分以上)的同学，其A级考试实际分数基本都是及格；高考成绩对学生的影响不大，这与时间间隔、课程性质都有关系[2]。该模型反映了大学英语日常教学与学生A级考试的关联性，可为教师教学改革提供可靠科学的依据。

表8 样本学生预测成绩与实际成绩对比 /分

三、 结论

本研究基于机电设备维修专业106位学生的英语成绩报表，构建多元线性回归模型来预测出每位学生在A级考试中可能取得的成绩，准确率可达83.3%。因此，教师依据预测结果对预测成绩较低的学生提出预警。其次，该模型各个自变量的系数表明了各个因素对考试成绩影响的大小，比如模型的回归系数表明卷面成绩每提高10分，A级成绩有望提高6.9分；平时成绩每提高10分，A级成绩有望提高4.9分，因此模型的建立也可为本校教师调整教学方法，提高课堂教学效果提供决策参考。

通过建立合理的成绩数据收集方法与成绩预测模型，可以科学、有效地预测英语A级考试成绩，能为教务管理、教学活动提供重要的决策参考。不足之处是运用该模型预测A级成绩时，存在个别学生的预测成绩与实际成绩之间差异较大的情况，所以在后续的研究中，应多考虑影响预测模型的各种因素，完善各项数据的收集工作，进一步优化预测模型[6]。