美国标准在水电站明钢管结构分析中的应用研究

任 杰 张 爽 杨丽娜

(中国电力建设集团昆明勘测设计研究院有限公司，云南 昆明 650051)

0 引言

压力钢管作为水电站的主要组成部分，其结构设计对整个电站的安全运行至关重要。由于设计规范思路的差异及语言困难，国内工程师在接触国际项目的初期往往不能快速熟悉美标规范的设计要求，因而影响项目的快速推进，故国外标准的熟悉程度对国际水电项目的实施存在一定的阻碍。本文结合工程实例对美标下的明管结构设计思路进行了整理，供国内工程师在短时间内了解美标的明钢管分析流程。

1 工程概况

某水电站采用引水式开发，正常水位1 718.5 m，最高水位1 728.2 m，涌浪水位1 762 m。该电站引水系统主要包括进水口、引水隧洞、调压井和压力钢管，压力钢管由埋管和明管组成，本文主要研究明钢管部分。明管段管径分别为2.2 m(主管)和1.5 m(支管)，其纵剖面见图1。计算中将明管段共分为6个断面进行分析，文中以进口No.1(桩号5+086.888)和出口No.6(桩号5+493.347)两个特征断面的结果进行说明。

2 结构计算

2.1 计算参数

根据招标文件要求明管钢板选用ASTM A516 GR70级钢[1]，明管结构分析的有关材料参数如表1所示。

表1 材料参数

2.2 计算工况

美标中将明管结构设计状况分为正常状况、临时状况、事故状况、非常状况、施工状况和水压试验状况，荷载组合共约25种[2]。结合规范[2]及招标文件要求，在确定壁厚方面设计工况共考虑两种：正常运行+水锤压力和水压试验工况。其中静压为涌浪水位与计算断面高程之差；根据招标文件要求，厂房处水锤为按0.2倍静压，各计算断面水锤考虑自厂房(最大点)至调压井(最小点0 m)的线性折减值；正常运行工况内压为静压与水锤之和；水压试验内压取正常运行情况最高内水压力值的1.25倍。工况内水压力取值见表2。

表2 计算参数

2.3 允许应力

美标规范采用提高系数与基本允许应力相结合的分析方法，综合考虑了不同的工作状况和应力类型，以最大剪切应力理论为主，压力钢管的应力分为一次应力、二次应力[3]。

美标中基本允许应力S取钢材1/3最小抗拉强度和2/3最小屈服强度中的较小值[3]。正常运行工况的放大系数K取1[2]，故正常运行工况的允许应力值为173.333 MPa。水压试验运行工况考虑放大系数K1取1.33[2]。

(1)

SN=K1×S=230.533

(2)

2.4 壁厚计算

压力钢管壁厚主要考虑两个方面：构造壁厚和结构壁厚，最终壁厚取两者大值。构造壁厚即为满足运输和吊装等所需的最小壁厚，结构壁厚为满足抵抗荷载所需的壁厚。美标中为满足运输和吊装等情况下所需的最小壁厚可采用太平洋电气公司及美国垦务局公式进行计算，并选择大值为最小壁厚。运输吊装壁厚如表3所示。

太平洋电器公司(PG&E)公式:

(3)

美国垦务局(USBR)公式:

(4)

满足运输和吊装的最小壁厚:

tmin=max(tmin1,tmin2) (5)

明管结构计算壁厚主要通过内压确定，故需进行正常运行+水锤压力和水压试验工况两种情况下的壁厚分析。美标结构壁厚由式(6),式(7)[2]确定。内水压力计算壁厚结果见表4，可见正常运行工况为控制工况，考虑到钢板生产的实际情况，断面No.1和No.6最终确定的计算壁厚分别为24 mm和20 mm。

(6)

(7)

其中，t为钢管壁厚，mm；P为内水压力,MPa；RA为计算断面处的钢管内半径mm；S为正常运行工况允许应力173.333 MPa；SN为水压试验工况允许应力230.533 MPa；E为焊缝折减系数，取1.0。

表4 计算壁厚

2.5 应力分析

明管结构应力分析包括管壁应力计算、支撑环应力计算及抗外压稳定计算。出于简化考虑，本文中仅对正常运行工况下的各部位应力进行计算。

2.5.1跨中及支撑环近旁管壁边缘弯曲应力计算

长距离钢管布置需设置相应支撑措施以满足钢管结构布置要求，在支撑作用下可将钢管假定为连续梁结构，而支座处的钢管会产生较大的应力导致钢管产生屈曲变形，故需根据最大剪应力理论[4]进行等效应力计算。两个部位的等效应力计算结果见表5，可见等效应力均小于允许应力，说明钢管壁厚满足要求。

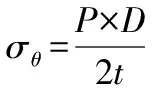
(8)

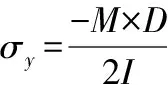
(9)

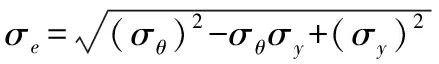
(10)

其中，D为钢管内径，m；I为管壁惯性矩，m4；σθ为环向应力，MPa；σy为纵向弯曲应力，MPa，底部拉力为+，顶部压力为-；σe为等效应力,MPa；M为支撑环处弯矩，kN·m。

表5 等效应力结果 MPa

2.5.2管壳局部弯曲应力

由于刚性的支撑环对钢管存在约束作用，在相邻的两个支撑环之间的钢管会产生纵向弯曲次应力。钢管在支撑环处发生变形时管壁不能像其他部位的钢管快速地进行应力扩散，因此在设计时需对支撑环与钢管共同作用情况下的最大弯曲应力进行计算复核。最大纵向弯曲应力采用式(11)进行计算，但首先应确定支撑环断面和支撑环支柱断面的特征值，如截面面积、中性轴至管壳内边缘的距离、面积矩和惯性矩等[2]，特征值计算简图如图2所示。断面No.1和No.6计算结果分别为135.05 MPa和135.153 MPa，均小于允许应力173.333 MPa。

(11)

其中，fb为管壳局部弯曲应力,MPa；Ar为支撑环横断面面积，m2；x4为支撑环宽度，m；y4为钢管计算壁厚，mm。

2.5.3重力作用和伸缩节位移产生的纵向应力

钢管通过支撑环及镇墩进行固定支撑，势必会由于抗滑作用产生各种力，因此在轴向压力作用下会发生薄壁管的直接屈曲或褶皱破坏。本文中的轴向力主要由钢管自重及管内水中自重沿轴向摩擦阻力和伸缩节变形两种效应组成，其中摩擦系数β取0.05，伸缩节轴力取1 000 N，分别计算得出断面No.1和断面No.6钢管截面应力f为-1.27 MPa和-0.141 MPa。

2.5.4支撑环应力分析

美标中针对支撑环应力分析是将支撑环与压力钢管相交处的环向应力与纵向应力进行组合，从而得到最大支撑环应力。其中分别包括有弯曲所引起的环向应力、内压下产生的直接应力、梁作用下钢管支座处的纵向应力和支座使钢管产生的弯曲应力，之后根据Hencky-von Mises的破坏理论对各种应力进行等效应力计算。

1)由内压产生的支撑环拉力可根据式(12)求得，断面No.1和断面No.6处分别为1 583.323 kN和1 125.489 kN。

(12)

2)支撑环近旁管壁应力通常在θ=0°,θ=180°,dMr/dθ=0和支撑点处最大[5]。本文中钢管支撑环采用下支撑形式，对应计算点共考虑4个，分别为θ=0°,θ=90°-,θ=90°+和θ=180°，竖向荷载计算系数见表6[5,6]，美标中对计算系数定义与国标一致。

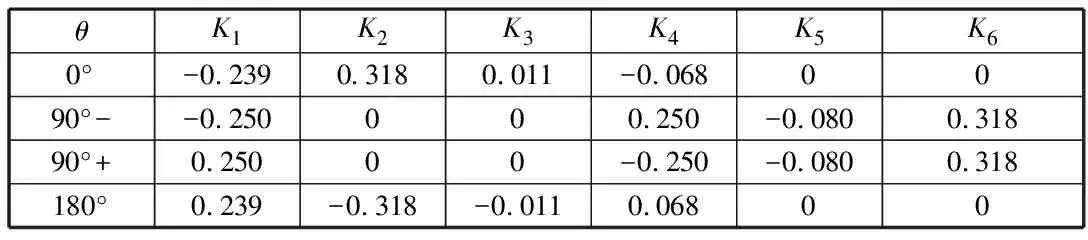
表6 竖向荷载系数

另外根据不同部位的计算系数可根据式(13),式(14)确定相应的推力T、弯矩M，进而根据内外侧应力式(15),式(16)求得不同计算点支撑环内外侧应力值，相应支撑环支柱截面特征值计算简图见图3。支撑环内外侧应力计算结果见表7。

表7 支撑环内外侧应力

T=Q(K1+BK2)

(13)

M=Q(RK3+xK4)

(14)

(15)

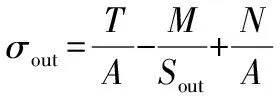
(16)

其中，A为支撑环截面面积，m2;Sin为支撑环内侧面积矩，m3;Sout为支撑环外侧面积矩，m3。

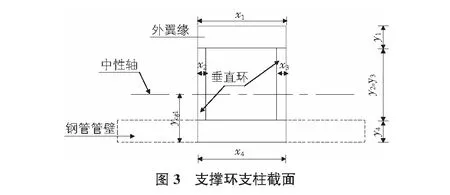
3)支撑环结构分析还需考虑在钢管自重和水重作用下四个点位的纵向弯曲应力fb1公式(17)，从支撑环顶部算起分别为0°,90°-，90°+及底部180°部位。纵向弯曲计算结果见表8。

(17)

其中，A为支撑环截面面积，m2；θ为0°，90°-，90°+，180°；I2为支撑环截面惯性矩，m4。

表8 纵向弯曲应力fb1

4)等效应力。

通过文中以上分析，支撑环的应力由钢管及水的自重、伸缩节及支座摩擦、近壁处局部弯曲应力和支撑环处纵向弯曲应力组成，轴线总纵向应力+支撑环纵向弯曲应力为以上所述的纵向应力数据之和(f+fb+fb1)。环向应力σx取支撑环内壁应力。进一步通过变形能量理论公式[6]得出支撑环处的等效应力，其计算结果见表9，可见结果小于允许应力173.333 MPa，正常运行工况下结构满足要求。

2.5.5抗外压稳定计算

为了防止明管在外压作用下产生变形破坏，需对管壁的抗外压强度进行分析比较确定是否采用加劲环来抵抗外压，如真空压力，本项目中真空压力取0.1 MPa。根据ASME UCS-28.2和UG-29抗外压计算规定[7]，现有管壁厚度下抗外压强度满足要求，且所需截面惯性矩足够，故不需另设加劲环。

表9 支撑环等效应力

3 最终壁厚确定

为了防止由于锈蚀、浸蚀、机械磨损或其他环境因素引起的钢管有效厚度变薄，需采取相应措施以满足结构要求[8]。一般需在计算壁厚的基础上考虑锈蚀厚度，本文取相应的锈蚀厚度为2 mm，此外也应采取相应的防腐措施如采用涂料、衬砌和阴极保护等延长钢管的使用寿命。两个断面最终壁厚分别取值为26 mm和22 mm。

4 结语

本文主要采用美国标准对水电站明钢管的结构分析流程进行了归纳总结，并以实际工程实例的计算过程对美标应用过程中的相应公式进行了介绍说明。美标中不仅对明管相关结构计算细节进行了注释，且对相关构造要求也规定了定量计算公式，如运输吊装最小壁厚，易于工程实践应用，具有较强的操作指导性。同时美标中允许应力相对国标取值较为保守，导致计算壁厚略大，工程安全裕度相应提高，但相比国标而言一定程度上增加了工程投资。