圆管输电塔风荷载多天平同步测力风洞试验研究

张宏杰， 黄 阳， 周 奇,3

(1. 中国电力科学研究院，北京 100055； 2. 汕头大学 土木与环境工程系，广东 汕头 515063；3. 汕头大学 广东省高等学校结构与风洞重点实验室，广东 汕头 515063)

输电塔线体系是电力系统中的输电载体，而输电塔一般采用格构式钢结构。随着国民经济水平的提高，高压、特高压输电体系在送电工程中越来越多地得到应用。这些输电塔高度高、塔距大、质量轻、刚度柔，对风荷载更为敏感。调查表明已有大量输电结构毁于风灾，而风荷载也成为了高压、特高压输电塔结构设计的控制荷载之一。20世纪80年代起，输电塔线抗风设计已是风工程界长期关注且至今未能很好解决的研究课题。

国际上，美国、加拿大、日本和澳大利亚等国风工程界对该课题进行了相关研究，并取得了阶段性成果[1-5]。国内风工程界也在输电塔-线体系动力计算模型与动力特性分析、风荷载模型与风振响应分析方法[6-7]、以及风洞试验[8-9]、现场实测等方面的研究取得了一些进展。但是，近几年的输电塔体系风毁事故说明了当前输电塔体系抗风研究和设计仍然存在着严重不足。不足之处主要表现在几个方面：①对横风向和扭转方向风荷载考虑不足。文献资料表明：输电塔横风向振动响应与顺风向相当，甚至比顺风向大，同时高压输电塔的扭转振动也不可忽略。②风荷载作用下输电导线的非线性效应考虑不足。输电导线类似于绳索结构，刚度低，质量小，发生振动时呈现出明显的非线性效应。同时，输电导线外形一般为圆形，且振动幅度大，导线与风的相互作用较为明显，使其风荷载的非线性效应十分显著。③风荷载作用下的塔线体系的耦合作用考虑不足。这里的耦合作用包括铁塔与导线之间的结构耦合、三维气动力之间的耦合和结构运动与气动力之间的耦合。由于耦合机理十分复杂，目前风工程界至今未能建立一种具有较高精度的格构式输电塔-线体系风振响应分析计算方法。④对于输电塔体系的三维风荷载考虑不足。目前对于输电塔体系的风荷载研究主要集中在水平风荷载作用研究，对于竖向风的作用研究十分少见。而实际工程中，台风、雷暴风、龙卷风等非良态气候强风一般都具有显著的竖向风分量。实际上，大量的风灾事故表明输电塔体系大多毁于非良态气候强风，由此可见竖向风作用可能也是不可忽略的因素之一[10-11]。

上述研究的不足之处中，对于第一个方面风工程界已经取得了一些研究进展，对于第二和第三个方面，由于问题复杂性和难度大，目前仍然没有取得突破性结果，而对于第四个方面，目前鲜有文献报道，该方面的研究几乎处于空白阶段。有鉴于此，本文采用多台微型高频动态天平同步测力方法对水平风和竖向风共同作用下的输电塔塔身结构的风荷载进行了风洞试验研究。

1 风洞试验介绍

1.1 试验模型

本文以某格构式圆管输电塔为研究对象，铁塔呼高为85.5 m，塔身的平面为正方形，全塔单线图如图1所示。

选取输电塔某段塔身为试验对象，塔身段位置如图1所示。试验模型几何缩尺比λR为1∶25，模型由上补偿段、测试段和下补偿段组成。模型总高为1.512 m，其中测试段高度为0.760 m，上补偿段高度为0.432 m，下补偿段高度为0.320 m。模型上补偿段顶端为正方形，边长为0.172 m，下补偿段底端亦为正方形，边长为0.460 m。模型测试段顶端为正方形，边长为0.240 m，底端亦为正方形，边长为0.396 m。模型四个边柱为圆柱形，外径为24.4 mm和22.4 mm，斜撑为边长7.8 mm的角钢和和外径为6.4 mm圆管，模型总实积率为0.233。试验模型采用薄钢管和薄角钢焊接制作而成，其中模型测试段的重量为3.65 kg(含天平端板)。为保证测力天平安装刚度，下补偿段钢管厚度适当加厚。

图1 输电塔单线图及节段模型位置(m)Fig.1 Line diagram of transmission tower and location of sectional model (m)

1.2 试验装置及测力系统

输电塔塔身节段模型测力风洞试验在汕头大学大气边界层风洞中进行。汕头大学边界层风洞是一座回流闭口式低速风洞，试验段尺寸为3.0 m(宽)×2.0 m(高)×20 m(长)。电机功率为450 kw，空风洞试验风速范围为1.0～45 m/s。流场不均匀性指标δU/U≤1.0%， 湍流度Iu≤1.0%， 气流竖向偏角Δα≤±1°， 水平偏角Δβ≤±1°。常规风洞试验中，通过旋转风洞转盘改变模型相对角度以模拟不同风向下风荷载作用，如模型垂直放置时，模拟风偏角的改变，模型水平放置时，模拟风攻角的改变。为了能在风洞里同时模拟不同风偏角和不同风攻角作用下的风荷载，本次试验设计了一个包含内框架和外框架的模型支撑系统，如图2所示。支撑系统的内框架和外框架均采用铝合金型材拼装而成，为了减少框架本身的气流绕流影响，铝合金型材选用了流线型阳极氧化铝合金型材。内框架和外框架通过钢转盘连接，改变钢转盘的连接角度可以实现内框架360°旋转。外框架通过底部钢板与风洞转盘固定连接，旋转转盘也可以实现整个模型支撑系统360°旋转。本次试验中，通过旋转风洞转盘改变作用在模型上的风偏角，而通过旋转内框架改变作用在模型上的风攻角。试验中，考虑到模型的对称性和减少模型支撑系统对试验模型的影响，风偏角的试验范围为0°～90°，且安装模型时，45°如图2所示，风攻角的试验范围为-30°～30°。模型安装时，首先将模型下补偿段底部端板与内框架底部端板固定连接，然后将测力天平固定在下补偿段模型顶部，接着连接模型测力段与测力天平，最后将模型上补偿段顶部端板与内框架顶部端板固定连接。为了保证模型测试段单独受力，模型上补偿段与模型测试段断开，并保留3 mm的间隙。

图2 风洞中支撑装置及试验模型Fig. 2 Supporting installation and test model in wind tunnel

测力系统由四个完全相同的独立高频动态天平，数据采集仪和计算机组成。高频动态天平采用美国ATI公司生产的高频动态天平，天平为圆柱形，直径为4 cm，高度为1.22 cm，重量为50 g。动态天平的量程和精度如表1所示，本次试验中采用的是SI-20-1型量程。

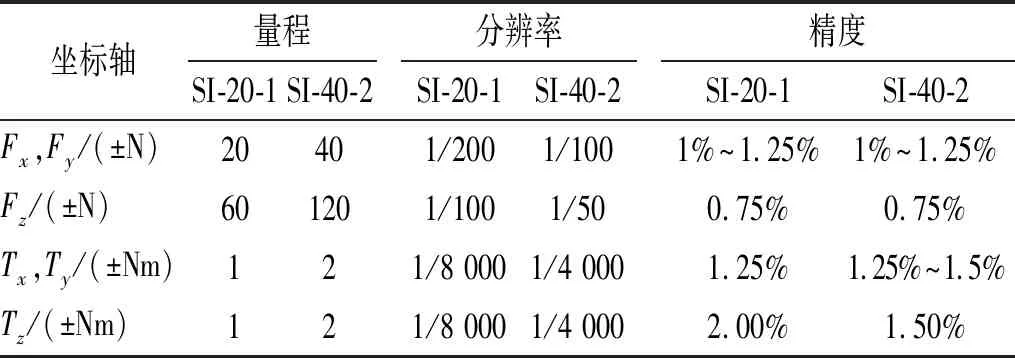
表1 高频动态天平参数表Tab.1 Parameters of high-frequency dynamic balance

2 风洞试验结果及对比验证

2.1 塔身六分力系数计算方法

坐标系XYZ为模型体轴坐标系，坐标原点位于模型底部中心。坐标系XiYiZi(i=1,2,3,4)表示第i个动态天平的局部坐标系，坐标原点位于天平中心。0°风攻角时，测力模型及高频天平的坐标系平面布置如图3所示，所有Z轴均与图3所示平面垂直，且遵循右手螺旋法则。0°风攻角时，风速方向与坐标轴X方向保持一致，Y轴在图3所示的平面内，且保证Z轴正向朝上。风偏角定义为模型X轴与平均风速U方向的夹角，且升力为负时偏角为正，图3所示亦为0°风偏角状态。风攻角定义为平均风速U方向与模型YOZ平面的夹角，且当竖向轴力为正时风攻角为正。根据上述坐标系统的定义，可以获得各个高频动态天平各力分量与模型各力分量之间的关系，具体可通过式(1)计算

图3 模型及天平坐标系示意图Fig.3 Definition of model and balance coordinate system

(1)

式中：Fb(b=x,y,z)为作用在模型XYZ轴方向上的气动力；Mb(b=x,y,z)为模型绕XYZ轴方向的气动力矩；fb(i)(b=x,y,z;i=1～4)为作用在动态天平XiYiZi轴方向上的气动力；mb(b=x,y,z)为动态天平绕xyz轴方向的气动力矩；x(i)和y(i) (i=1～4)分别为动态天平中心处坐标值。风轴下气动力和气动力矩可以通过式(2)换算获得

Fw=TbwCFb,Mw=TbwCMb

(2)

式中：Fw为风轴下气动力矢量矩阵；Fb为体轴下气动力矢量矩阵；C为多天平系统标定矩阵；Mw为风轴下气动力矩矢量矩阵；Mb为体轴下气动力矩矢量矩阵；Tbw为气动力和气动力矩由体轴向风轴转换的转换矩阵。转换矩阵可按式(3)计算

(3)

式中：θ为风攻角；β为风偏角。获得模型体轴和体轴下作用气动力和气动力矩后，无量纲平均六分力系数可按式(4)计算

(4)

式中：Cw(w=p,h,q)为风轴下平均气动阻力系数、平均气动升力系数和平均气动轴力系数；CMw(w=p,h,q)为风轴下平均气动摇摆力矩系数、平均气动俯仰力矩系数和平均气动偏转力矩系数；V为试验平均风速；H为模型高度；Bs为0°风偏角时的模型投影宽度，本次试验取48.8 mm；Bf为0°风偏角时的力臂宽度，本次试验取396 mm。

2.2 不同风速下试验结果对比

对于圆形截面，气流流经后的绕流状态跟雷诺数有关，输电塔塔身四个边柱和部分斜撑均为圆形截面，为了考虑雷诺数效应和试验精度，本次试验中共进行了五种试验风速，即5 m/s，10 m/s，15 m/s，20 m/s和25 m/s。根据雷诺数的计算公式Re=VD/υ，式中：D为构件外直径；υ为空气比例黏性系数，取值1.46×10-5m2/s，计算的雷诺数结果如表2所示。

表2 不同试验风速下圆形杆件的雷诺数计算结果Tab.2 Renold numbers of tubular members under different wind speeds

图4为输电塔塔身在不同试验风速下平均气动力系数随风偏角变化的试验结果。从图中可以看出，所有气动力系数随风偏角的变化趋势基本一致。试验风速为5 m/s时，平均气动阻力系数、平均气动升力系数和平均气动轴力系数的试验结果均要明显大于试验风速为10 m/s，15 m/s和20 m/s的试验结果；平均气动摇摆力矩系数和气动平均偏转力矩系数要明显小于试验风速10 m/s，15 m/s和20 m/s试验结果，而气动平均俯仰力矩系数则大于试验风速为10 m/s，15 m/s和20 m/s的试验结果。查询试验测试数据发现，此时最小的平均气动力只有0.2 N左右，而试验天平的测试精度为0.2～0.25 N，表明测试精度较低。观察试验风速25 m/s的试验结果时发现，平均气动阻力系数和平均气动俯仰力矩系数的测试结果要略大于试验风速为10 m/s，15 m/s和20 m/s的试验结果，而其他平均气动力系数的测试结果与试验风速为10 m/s，15 m/s和20 m/s的试验结果偏差不大。查看数据发现各天平测试获得的阻力根方差为0.8 N左右，表明该风速下模型的振动将对试验结果有一定的影响。如表2所示，测试段的圆管雷诺数均处于亚临界范围(即Re<4×104)。Schewe[12]和ASCE[13]研究表明，当雷诺数处于Re<5.5×104和Re<2×104时，阻力系数会随着试验风速的增大而增大。但试验中发现，当试验风速为10 m/s，15 m/s和20 m/s时，天平测试获得的模型升力系数几乎完全重合，而阻力系数也相差不大，如图4所示。这表明当前试验雷诺数范围内，雷诺数效应对该塔身平均六分力系数影响可以忽略，这可能是因为测试段中的角钢存在，影响了整个测试段的气流扰流所致。

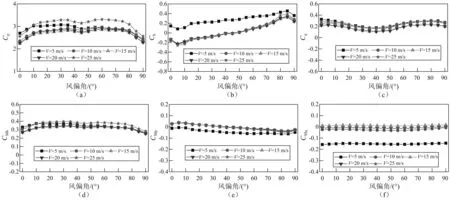
图4 不同风速下塔身节段气动力系数试验结果Fig.4 Test results of aerodynamic coefficients of tower sectional model under different wind speeds

2.3 对比验证试验

为了验证多天平同步测力试验方法的可靠性，本文还进行了两种常规节段模型测力风洞试验，对0°风攻角下不同风偏角的塔身六分力系数进行测量。图5为对比试验1的风洞试验照片，图6为对比试验2的风洞试验照片。如图所示，对比试验1和对比试验2均通过支撑框架的方式悬吊上补偿模型，不同于对比试验2，对比试验1还设置了分离平台，模型测试段安装与分离平台上以减少风洞地面边界层效应。

图5 对比试验1Fig.5 No.1 contrast experiment

图6 对比试验2Fig.6 No.2 contrast experiment

图7为0°风攻角下输电塔塔身气动力系数三种风洞试验结果对比。从图中可以看出，塔身气动力系数随风偏角的变化特征基本一致，且气动力系数与其对应的气动力矩系数变化规律一致。对于阻力系数，对比试验1和多天平试验结果较为接近，相差不大，而对比试验2试验结果明显小于前两者。这主要是因为风洞边界层效应导致风洞近地面的来流风速要小于远离风洞地面处风速的原因。对于升力系数，对比试验1和对比试验2的试验结果基本一致，而多天平试验结果的数值要略大于前两者。这可能是因为多天平试验中装有下补偿段模型，产生升力的气流扰流存在三维特性，而在对比试验1和对比试验2中未安装下补偿模型，气流扰流被分离成准二维流动。也即，多天平试验中计入了气流扰流的三维效应，对比试验1和对比试验2未能计入。对于竖向轴力系数，多天平试验和对比试验1的试验结果均接近于0，而对比试验2试验结果要大于前两者。实际上，对于0°风攻角的水平风作用下，竖向轴力应当接近0，对比试验2的结果表明由于边界层效应的存在，风洞近地面气流存在一定的正攻角，这导致了对比试验2的试验结果明显大于0。

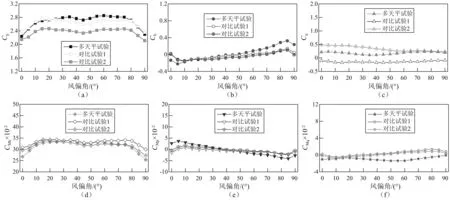
图7 0°风攻角下不同试验方法的气动力系数Fig.7 Aerodynamic coefficients under tilt angle of 0° via different test methods

综上所述，通过两种常规试验的对比验证了多天平同步测力风洞试验的可靠性。同时，相比于对比试验，多天平试验还存在以下优点：①避免了风洞边界层效应的影响；②同时安装上下补偿段，可以准确模拟塔身气流扰流的三维效应；③可以避免使用大端板进行风洞试验；④可以进行水平风和竖向风联合作用下的风荷载测试；⑤在某些试验中可以直接测量风荷载，而不需要通过两次试验结果相减的方法获得部分构件风荷载，如横担、塔头等。

3 竖向风对塔身风荷载的影响

图8为不同风攻角下输电塔塔身气动力系数试验结果。从图中可以观察到几点特征：①气动力系数随风攻角的变化规律与其对应的气动力矩系数变化规律保持一致。如，阻力系数和俯仰力矩系数随风攻角的改变均呈现出余弦函数变化特征。②不同风偏角下气动力系数随风攻角变化的改变大小不同。如30°和60°风偏角下气动力系数的变化幅度要明显大于0°和90°风偏角下的变化幅度。③由于结构的对称性，气动力系数具有关于一定风攻角和风偏角的对称性。如，气动力系数明显关于0°风攻角对称，其对称性的差别主要是由于输电塔塔身结构呈台柱状的原因，塔身上部结构尺寸要小于塔身下部结构尺寸。又如，不同风攻角下阻力系数均关于45°风偏角对称，这与输电塔结构对称性是一致的。

图8 不同风攻角下塔身节段气动力系数试验结果Fig.8 Test results of aerodynamic coefficients of tower sectional model under different tilt angles

考虑到输电导线与输电塔结构的连接方式，0°，30°，45°，60°和90°均是输电塔结构风荷载设计的关键角度。为此，本文对上述关键风偏角下不同风攻角的阻力系数进行了对比分析。表 3列出了主要风偏角下不同风攻角的阻力系数对比。Bayer的研究表明，在-10°～45°风偏角和0°～15°风攻角范围内，风攻角对输电塔阻力系数的影响小于3%。从表中可以看出，上述角度范围内，风攻角引起的阻力系数最大偏差为-6.7%，高于Bayer的研究结论。在-5°～5°风攻角范围内，风攻角引起的阻力系数最大偏差为-5.3%，风攻角对输电塔阻力系数的影响较小，可以忽略。但在-30°～30°内，风攻角引起的阻力系数最大偏差为-21.3%，已超出Bayer的研究结论。

表3 主要风偏角下不同风攻角阻力系数对比Tab.3 Comparison of drag coefficients under some key yaw angles between different attak angles

由此可见，在风攻角不大的来流风作用下，风攻角对输电塔阻力系数的影响不大，可以忽略。然而，实际工程中有大量输电塔位于山区地形，位于山坡或山顶的输电塔会遭受带有较大风攻角的斜坡风作用。又如，台风、雷暴风或者龙卷风等强风都是典型的三维风，同时具有水平风荷载和竖向风荷载成分。此时，输电塔风荷载计算中有必要考虑风攻角对气动力系数的影响。

4 结 论

本文采用多台微型动态天平同步测力的方法对格构式输电塔不同风攻角和风偏角作用下的平均气动力系数进行考察。获得以下几点结论：

(1) 本文设计的模型支撑框架系统及多台微型动态天平同步测力技术可以直接测量输电塔塔身风荷载，同时微型动态天平安装在补偿段模型可以直接测试输电塔结构中构件风荷载，如横担、塔头等。

(2) 不同试验风速下的试验结果表明，当前雷诺数范围内，输电塔塔身平均气动六分力系数的雷诺数效应不是很显著，但为了确保试验精度，应选择合适的试验风速避免信噪比太小或模型振动幅度太大。

(3) 对比试验验证了多天平同步测力方法的可靠性。多天平同步测力方法可以同时模拟不同风攻角和风偏角，也更为准确地模拟气流扰流，能减少或避免风洞地面或分离平台产生的边界层效应。

(4) 在±5°的风攻角范围内，风攻角对阻力系数的影响较小，可以忽略。但在±30°的风攻角范围内，风攻角引起的阻力系数偏差最大达到20%左右，不可忽略。因此，对于来流风具有明显竖向风分量时，有必要考虑风攻角对输电塔塔身气动力系数的影响。