全国名校抛物线测试卷答案与提示

一、选择题

1.C 2.B 3.B 4.C 5.D 6.A 7.C 8.B 9.A 10.B 11.C 12.B 13.A 14.B 15.B 16.C 17.C 18.C 19.D 20.C 21.C 22.B

二、填空题

23.2 24.(5,4) 25.y2-4y+2x=0 26.6 27.28.6 29.230.32

三、解答题

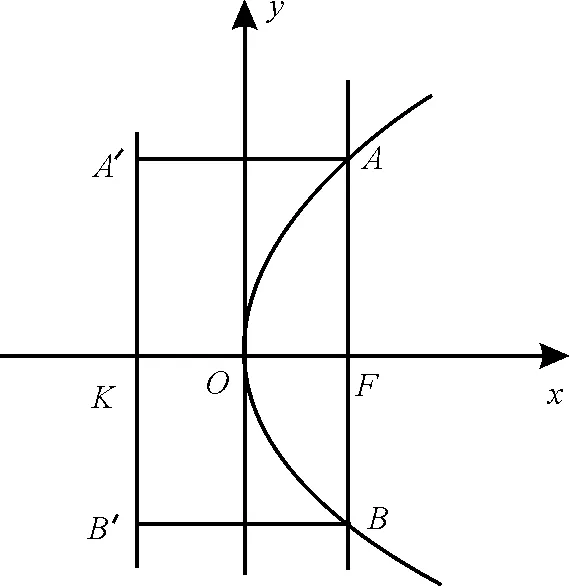
图1

31.(1)设抛物线的准线为l,交x轴于K点,l的方程为x=。如图1,作AA′⊥l,BB′⊥l,则|AF|=|AA′|=|m|。同理,|BF|=|m|。又|AB|=6,则|2m|=6,m=±3,所求抛物线方程为y2=±6x。

(2)设焦点为F(a,0),|PF|==6,即a2+10a+9=0,解得a=-1或-9。当焦点为F(-1,0)时,p=2,抛物线开口方向向左,其方程为y2=-4x；当焦点为F(-9,0),p=18,抛物线开口方向向左,其方程为y2=-36x。

32.点M到对称轴的距离为6,可设点M的坐标为(x,6)。

又因为点M到准线的距离为10,所以

故当点M的横坐标为9时,抛物线方程为y2=4x；当点M的横坐标为1时,抛物线方程为y2=36x。

33.设弦两端点分别为P1(x1,y1),P2(x2,y2)。

因为P1,P2在抛物线上,所以=6x1,=6x2。

两式相减,得：

(y1+y2)(y1-y2)=6(x1-x2)。

因为y1+y2=2,所以k=

故直线的方程为y-1=3(x-4),即3x-y-11=0。

则y1+y2=2,y1·y2=-22。

故|P1P2|=

34.将y=kx-2代入y2=8x,变形整理得：

k2x2-(4k+8)x+4=0。

设A(x1,y1),B(x2,y2)。

由题意得x1+x2==4⇒k2=k+2⇒k2-k-2=0。

解得k=2或k=-1(舍去)。

由弦长公式得：

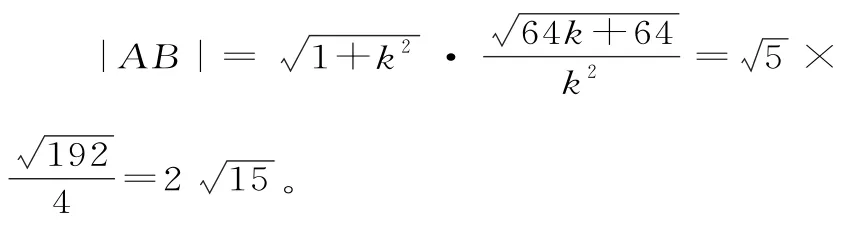
35.设AB方程为y=x+b。

x2+(2b-8)x+b2=0。

设A(x1,y1),B(x2,y2),则：

x1+x2=8-2b,x1·x2=b2。

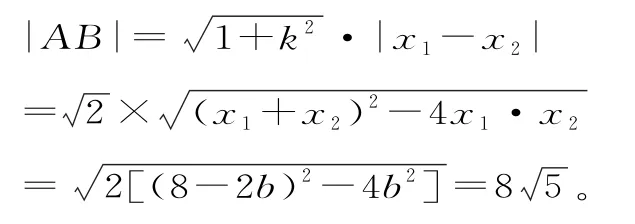
解得b=-3。

直线方程为y=x-3,即x-y-3=0。

焦点F(2,0)到x-y-3=0 的距离为

故S△FAB=

36.(1)点P与点F(2,0)的距离比它到直线x+4=0 的距离小2,所以点P与点F(2,0)的距离与它到直线x+2=0 的距离相等。

由抛物线定义得：点P在以F为焦点,直线x+2=0为准线的抛物线上,抛物线方程为y2=8x。

(2)①若l斜率存在,设直线l：y=kx+b与抛物线交于点(x1,y1),(x2,y2)。

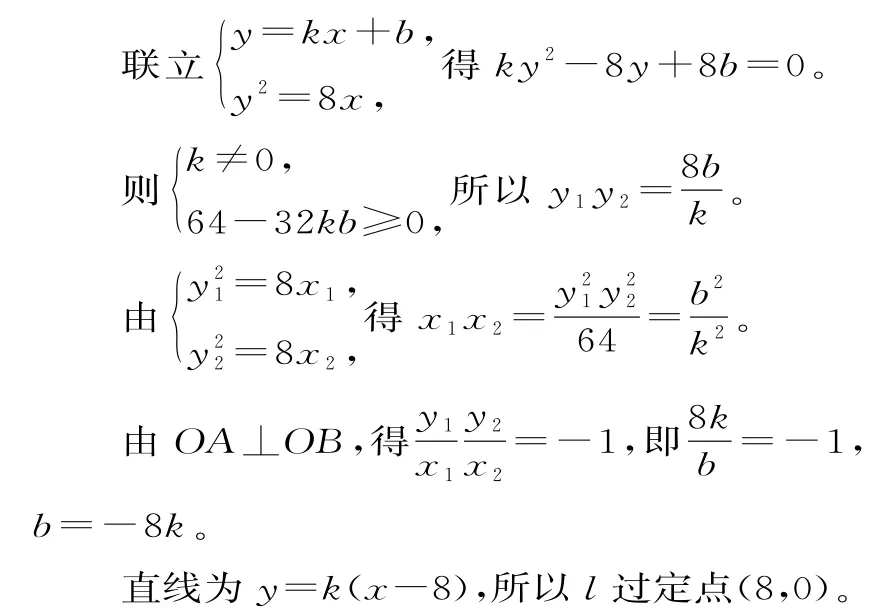
②直线l与x轴垂直,则直线OA或直线OB的斜率为1。

直线l过定点(8,0)。

由①②得：直线恒过定点(8,0)。

37.(1)设A(x1,y1),B(x2,y2),则x1+x2=6。

由抛物线的定义知|AF|=x1+1,|BF|=x2+1,|AF|+|BF|=x1+x2+2=8。

(2)设直线l的方程为x=my-1,由得y2-4my+4=0。

由Δ=16m2-16＞0,得m2＞1。

则y1+y2=4m,y1y2=4。

由抛物线的定义知|AF|=x1+1,|BF|=x2+1,则|AF|·|BF|=(x1+1)(x2+1)=m2y1y2=4m2。

因为m2＞1,所以|AF|·|BF|＞4。

故|AF|·|BF|的取值范围是(4,+∞)。

联立直线方程与y2=2px(p＞0)得：

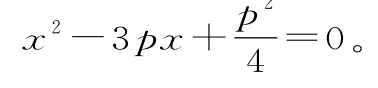
设M(x1,y1),N(x2,y2),则有x1+x2=3p。

因为|MN|=8,所以x1+x2+p=8,即3p+p=8,解得p=2。

抛物线C的方程为y2=4x。

(2)设l的方程为y=x+b,代入y2=4x,得x2+(2b-4)x+b2=0。

因为l为抛物线C的切线,所以Δ=0。

解得b=1,l：y=x+1。

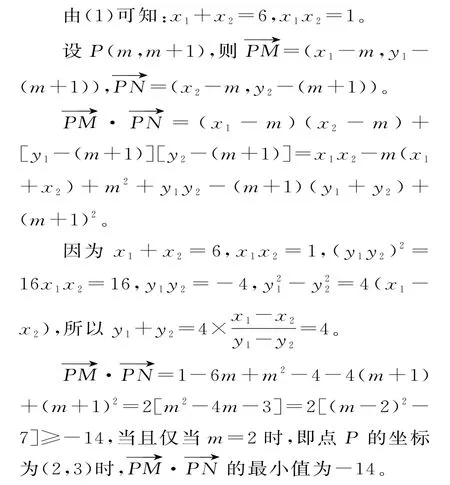
(2)设直线AB与x轴交于点N,显然k≠0,点N的坐标为(-1,0)。

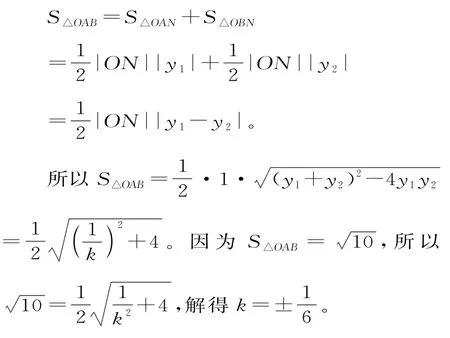
40.(1)当l与x轴垂直时,l的方程为x=2,代入y2=2x,解得M(2,-2),N(2,2)或M(2,2),N(2,-2)。故BM的方程为2y+x+2=0或x-2y+2=0。

(2)如图2,设MN的方程为x=my+2,M(x1,y1),N(x2,y2)。联立方程得：

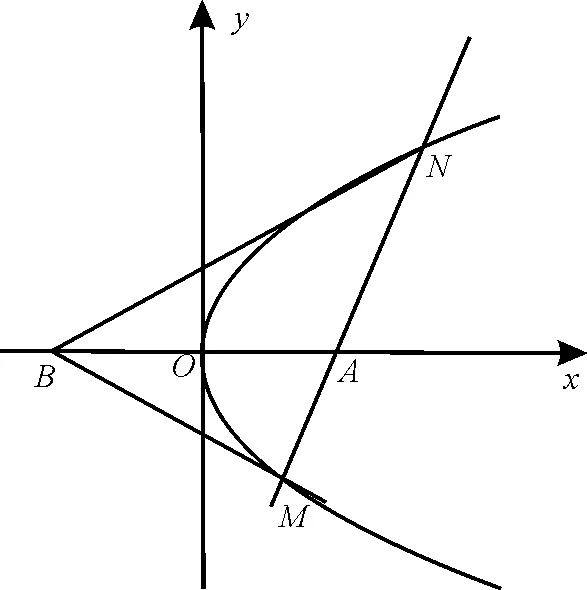
图2

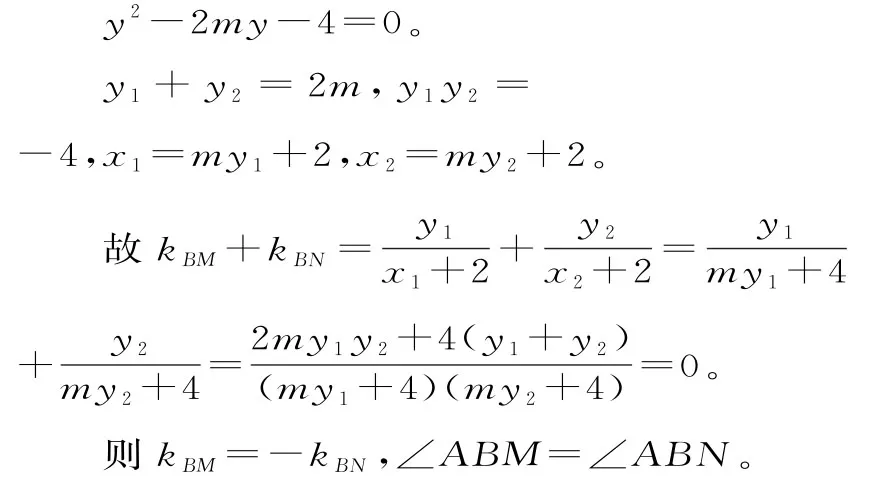
41.(1)设直线l方程为：y=x+m,A(x1,y1),B(x2,y2)。

由抛物线焦半径公式可知：|AF|+|BF|=x1+x2+=4,故x1+x2=。

9x2+(12m-12)x+4m2=0。

则Δ=(12m-12)2-144m2＞0,m＜。

则x1+x2=,解得m=。

直线l的方程为,即12x-8y-7=0。

(2)设P(t,0),则可设直线l方程为：

42.(1)设A(x1,y1),B(x2,y2),则x1≠x2,y1=,x1+x2=4。

于是直线AB的斜率k=

(2)不妨设过点M的切线方程为y=x+b,联立y=,可得b=-1,切点的横坐标为2。

设M(x3,y3),则x3=2,于是M(2,1)。

设直线AB的方程为y=x+m,线段AB的中点为N(2,2+m),|MN|=|m+1|。

将y=x+m代入y=得：

x2-4x-4m=0。

当Δ=16(m+1)＞0,即m＞-1时,不妨设方程两个根,x1=2+2,x2=2-2。

从而|AB| =|x1-x2| =4。

由题设知|AB|=2|MN|,即4=2(m+1),解得m=7。

所以直线AB的方程为y=x+7。

43.(1)依题意知F(1,0),设直线AB的方程为x=my+1。

将直线AB的方程与抛物线的方程联立,消去x得y2-4my-4=0。

设A(x1,y1),B(x2,y2),所以y1+y2=4m,y1y2=-4。①

联立①和②,消去y1,y2,得m=。

所以直线AB的斜率是±。

(2)由点C与原点O关于点M对称,得M是线段OC的中点,从而点O与点C到直线AB的距离相等,所以四边形OACB的面积等于2S△AOB。

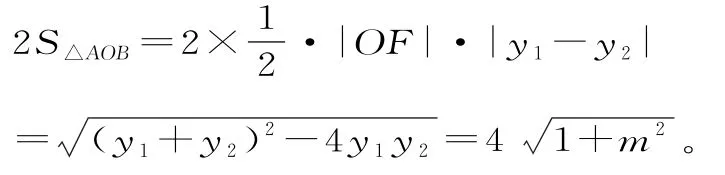
当m=0时,四边形OACB的面积最小,最小值是4。