对角相似变换下的非负矩阵最大特征值算法
2019-11-28王信存吕洪斌商钰莹
王信存,吕洪斌,商钰莹
(1.辽东学院 师范学院,辽宁 丹东 118003;2.北华大学 数学与统计学院,吉林 吉林 132013)
1 引言与预备知识
非负矩阵在计算数学、线性规划、计算机科学技术、自动控制等领域应用广泛[1-3],非负矩阵最大特征值的估计与计算是非负矩阵理论中的经典内容,在数值代数中具有重要意义.
设Mn()和Mn()分别表示实数域和复数域上的n×n阶矩阵集合,N={1,2,…,n},+表示正整数集合.设A=(aij)∈Mn(),记表示矩阵A的有向图,C(A)表示Γ(A)的简单回路集合,σ(A)表示矩阵A的谱集,表示矩阵A的谱半径,表示n阶正对角矩阵的集合,E表示单位矩阵.若A=(aij)∈Mn(),且aij≥0(i,j∈N),则称A为非负矩阵,记为A∈Mn(+).设A∈Mn(+),由Perron-Frobenius定理[1,4]知ρ(A)∈σ(A),称为非负矩阵A的最大特征值,也称ρ(A)为非负矩阵A的Perron根.对A=(aij)∈Mn(+),α∈,记A(α)=A+αE,ri(A(α))=ri(A)+α∶=ri(α),i∈N.
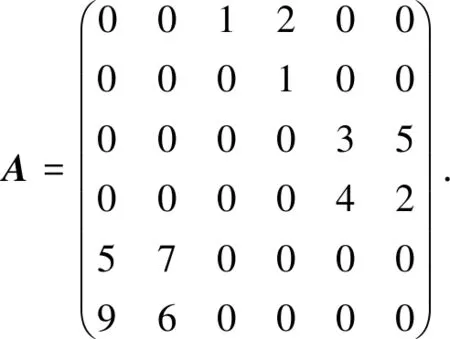
定义1[1,4]设矩阵A=(aij)∈Mn(),如果存在n阶置换矩阵P,使得其中A11为r×r阶矩阵(1≤r 设A=(aij)∈Mn(+)不可约,Ax=ρ(A)x,x∈n,则x可取为正向量,且当‖x‖1=1时称x为A的Perron向量[4]. 目前,关于不可约非负矩阵最大特征值的计算已有很多成果,如: 文献[5]给出了13种具体算法,对不可约非负矩阵最大特征值的计算进行了系统研究;文献[6-7]的算法适用于不可约非负矩阵,但涉及指数运算;文献[8-10]给出的算法适用于一类不可约非负矩阵,即对角元素均非零或至少有一个非零元素的本原矩阵.本文给出一类基于对角相似变换的不可约非负矩阵最大特征值和对应特征向量的算法,结果表明,该算法计算简洁,并适用于所有不可约非负矩阵. 定理1(Perron-Frobenius定理)[4]设A=(aij)∈Mn(+),ρ(A)是A的最大特征值,则 设A=(aij)∈Mn(+)是不可约的,记不妨设r(0) 类似于文献[7,9]的证明,有: 引理1设A=(aij)∈Mn(+)不可约,∀γ∈C(A),记γ:i1→i2→…→ir→ir+1=i1,则∀m∈+,有 引理2设A=(aij)∈Mn(+)不可约,ρ(A)是A的最大特征值,不妨设r<ρ(A) 证明:由定理1,显然有r(m)≤ρ(A)≤R(m),m∈+∪{0},而 证毕. 类似文献[7,9]的证明,有: 引理3设A=(aij)∈Mn(+)不可约,如果aij>0(i,j∈N),则 由引理3知 定理2设A=(aij)∈Mn(+)不可约,ρ(A)是A的最大特征值,则在上述矩阵序列和记号下,有 由式(1),类似地有 进一步有 因此,∀i∈N,有 进一步,∀k∈+,有 下面考虑不可约非负矩阵A=(aij)∈Mn(+)的Perron向量的数值算法.记 定理3设A=(aij)∈Mn(+)不可约,ρ(A)是A的最大特征值,则n是A的相应于ρ(A)的正特征向量,进而可得A的相应于ρ(A)的Perron向量. 根据上述迭代矩阵的构造过程和定理2,下面给出本文的算法. 算法1计算不可约非负矩阵最大特征值算法. 输入: 不可约非负矩阵A=(aij)∈Mn(+),0<ε<1; 步骤3) 令di=ri+θ(rmax-ri),D=diag(d1,d2,…,dn),D-1AD∶=A,转步骤1). 由定理2知,算法1适合所有不可约非负矩阵最大特征值的计算,且适用范围广、简单实用. 例1随机构造循环指数为3的不可约非负矩阵: 对于矩阵A,文献[8,10]的算法不能直接应用,而文献[9]的算法需考虑矩阵A+E6.表1列出了应用本文算法、文献[5]的第九个算法(取γ=0.8)和文献[9]的算法计算矩阵A最大特征值的迭代次数比较结果. 表1 不同算法计算ρ(A)的迭代次数比较 由表1可见,本文算法不但适用于所有不可约非负矩阵最大特征值及对应特征向量的计算,而且参数的选择更方便,并且在适当的参数选择下效率较高. 设A=(aij)∈Mn(),若则称A为严格对角占优矩阵[3-4];若有正对角矩阵D=diag(d1,d2,…,dn),使得AD为严格对角占优矩阵,则称A为广义严格对角占优矩阵.设A=(aij)∈Mn(),其中: ∀i∈N,aii>0;∀i≠j,i,j∈N,aij<0.则A可写成A=sI-B,s>0,B∈Mn(+).如果s>ρ(B),则称A为非奇异M-矩阵[1,3].这是M-矩阵的一个等价表征[1,3],且M-矩阵的按模最小特征值是一个正数.设A=(aij)∈Mn(),记m(A)=(mij)∈Mn(),其中: ∀i∈N,mii=|aii|;∀i≠j,i,j∈N,mij=-|aij|.则称m(A)为A的比较矩阵[3].设A=(aij)∈Mn(),则A为广义严格对角占优矩阵的充要条件是A的比较矩阵m(A)为非奇异M-矩阵[3].因此,若A=(aij)∈Mn()为M-矩阵,将A写成A=sI-B,s>0,B∈Mn(+),则M-矩阵的最小特征值为s-ρ(B).因此,由M-矩阵的等价表征,应用非负矩阵最大特征值和对应特征向量的算法可以给出广义严格对角占优矩阵(M-矩阵)的迭代判别法、M-矩阵最小特征值及其对应特征向量的算法.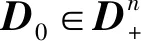
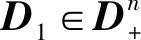
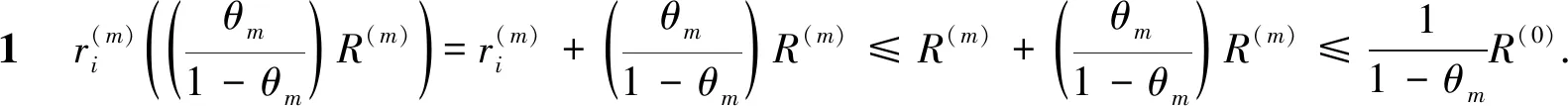


2 主要结果


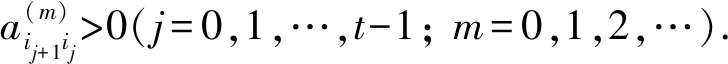




3 算法及分析

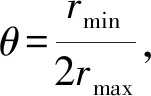

4 应 用
