海洋天然气水合物层钻水平井不同扩径方式携岩能力图版

魏纳 刘洋 崔振军 江林 李海涛 徐汉明

油气藏地质及开发工程国家重点实验室·西南石油大学

天然气水合物(俗称“可燃冰”)作为清洁能源，主要分布于陆地永久冻土带和沿海300～3 000 m水深海域，其中大约90%储存在深海区域［1-2］。据不完全统计，全球天然气水合物蕴藏资源总量约为2.1×1016m3，我国天然气水合物的资源总量大约为80.1×1012m3，其中南海海域、东海海域的资源总量分别为 64.2×1012m3、3.38×1012m3［3-4］。从 2007、2013、2017年中国海域已经取样的水合物储层来看，其多存在于海底以下300 m 内的浅层软泥砂里(层厚10～70 m)，储层欠压实、弱胶结、没有常规油气藏致密盖层［4-6］。面对如此巨大的资源量，如何高效安全开发海洋天然气水合物一直是我国乃至全球的研究热点。

根据我国海洋天然气水合物埋深浅、层薄、欠压实、弱胶结的成藏特点，长水平井可能是未来商业化开发的有效模式。这种井型主要优势在于大幅度延伸了井眼轨迹、适合开发我国南海薄层状水合物藏［7-9］。但在钻水平井过程中，当钻头破碎岩层后，原有欠压实、弱胶结的储层应力状态被打破后易发生井眼坍塌、扩径。因此，笔者通过选取不同井眼扩径角为直角、45°斜角、圆弧的模型，针对不同颗粒粒径、水合物丰度等条件进行模拟仿真，深入研究海洋天然气水合物层钻水平井不同扩径方式对携岩能力的影响，这对合理设计钻井工艺参数、保证安全钻井具有重要实际意义。

1 模型建立及边界条件设定

1.1 理论模型

为建立本文研究的数学模型，作以下几点假设：模型中流体的流动具有定常、均匀的性质；进行模拟分析时不考虑钻柱的旋转与偏心；模型中流体当作不可压缩的流体处理。在上述基本假设条件下，采用的数学模型为多相流模型和湍流模型［10］。

(1)多相流模型。

连续性方程

动量方程

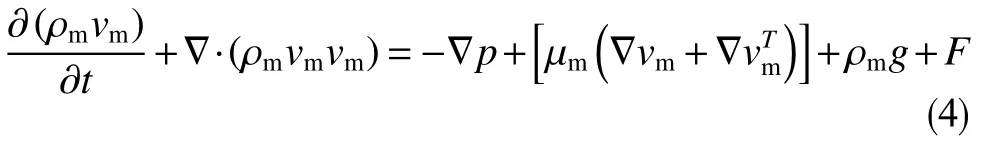
式中，vm为多相流的平均速度，m/s；ρm为多相流的平均密度，kg/m3；αk为第k相的体积分数；ρk为第k相的速度，m/s；μm为多相流的黏度，Pa · s；F为体积力，N。

(2)湍流模型。

湍流模型采用标准κ-ε模型［11］，湍流动能方程 (κ方程)为

耗散方程 (ε方程)为

式中，Gκ为平均速度梯度引起的湍动能κ的产生项，N/(m2· s)；Gb为浮力影响引起的湍动能κ的产生项，N/(m2· s)；YM为可压缩湍流脉动扩张对总的耗散率的影响，kg/(m · s3)；μt为湍动黏度，Pa · s；C1ε、C2ε、C3ε为经验常数，FLUENT 中默认值为C1ε=1.44、C2ε=1.92、C3ε=0.09；σκ、σε分别为湍动能和耗散率对应的普朗特数，FLUENT 中默认值为σκ=1.0、σε=1.3。

1.2 几何模型

天然气水合物层钻水平井水平段中3 种不同扩径方式的实体模型均利用Creo2.0 软件进行建模(图1)。实体模型的井身结构基础数据以某水平井为例：环空内径0.13 m，外径0.2 m，水平段总长4.5 m，直角段扩径处长度1 m，直径0.3 m，扩径率为1.5 倍。

图1 水平段扩径模型Fig.1 Hole enlargement model for horizontal section

将实体模型导入到FLUENT 中的Models 进行设置边界条件：(1)水合物密度为950 kg/m3，岩屑密度为2 600 kg/m3；(2)因为在水平段内运动时温度和压力变化不大，水合物颗粒分解量很小，因此不考虑水合物颗粒的分解率。

从具体实施内容来讲，智能楼宇通常包括安防监控、出入口控制（门禁、停车场）、入侵防范、电梯控制、供配电、空调新风、照明控制、停车场管理、广播、信息发布和能耗统计等数十个信息化子系统，业内将上述子系统归纳为五类，分别是建筑设备自动化（BA）、通讯自动化（CA）、办公自动化（OA）、火灾报警与消防自动化（FA）以及安全防范自动化（SA），即智能楼宇5A系统[2]。

2 仿真分析

2.1 水合物丰度10%及粒径4 mm 时携岩临界流速

设置模型的边界条件水合物丰度为10%，含水合物的岩屑颗粒粒径为4 mm 且每秒生成3 000 个颗粒，通过加权平均计算得到颗粒密度为2387.5 kg/m3，转速为30 rad/s，钻头直径为215.9 mm，模拟仿真后得到3 种不同扩径方式下携岩的临界流速，其颗粒分布如图2 所示。

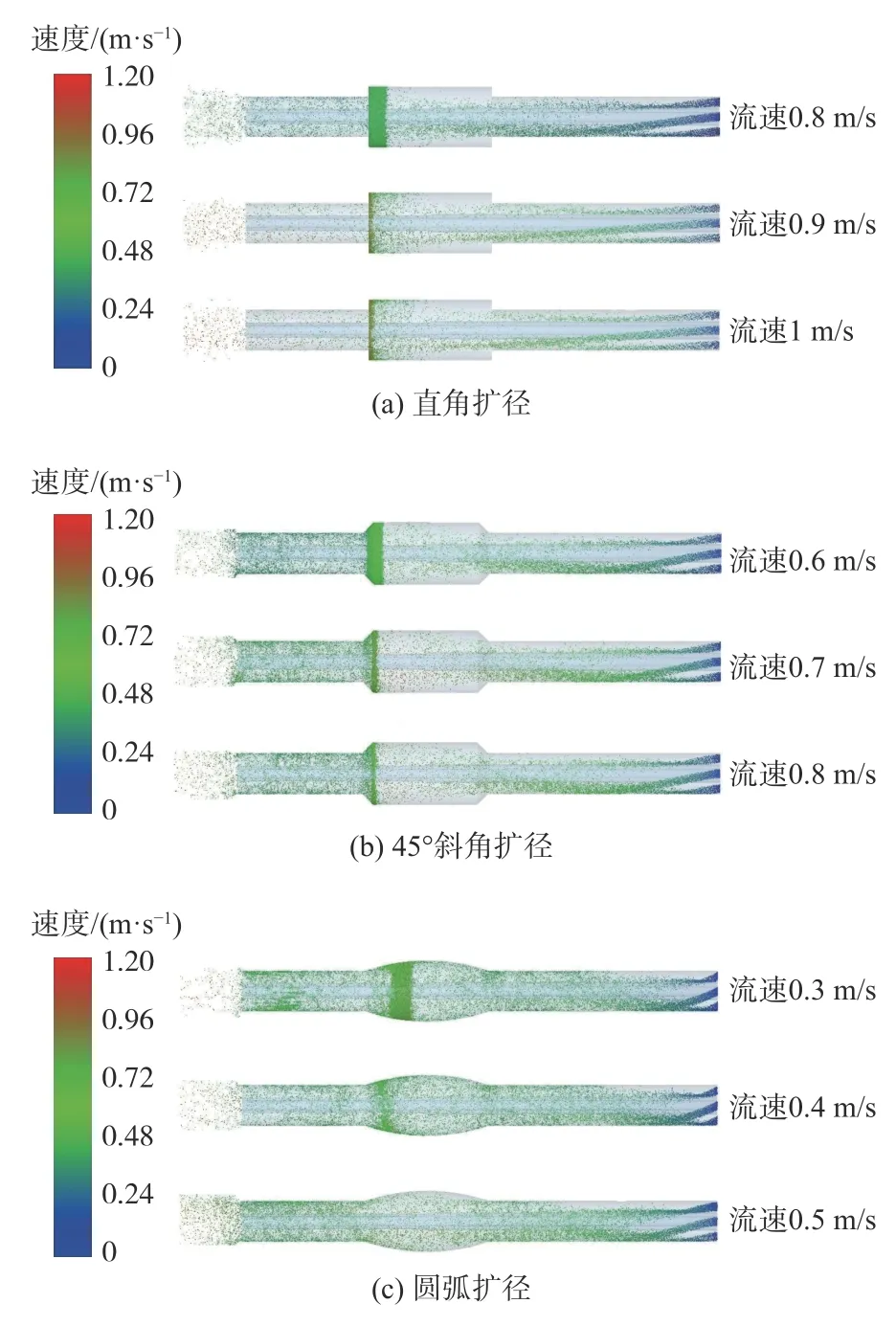
图2 不同流速携岩颗粒分布图Fig.2 Distribution of cuttings carrying particles with different flow velocities

从图2 可看出：对于直角扩径方式，当钻井液流速0.8 m/s 时，直角扩径段的左边堆积了大量颗粒；当钻井液流速0.9 m/s 时，直角扩径段的左边堆积的颗粒已经明显减少；当钻井液流速1 m/s 时，直角扩径段的左边堆积的颗粒数量与流速0.9 m/s 堆积的颗粒数量基本相同。造成这种现象主要是由于钻井液流速增大，使得钻井液对岩屑颗粒的拖拽力增大，从而使更多的岩屑颗粒流出直角扩径段。对于45°斜角扩径而言，相比直角扩径，岩屑颗粒更容易从斜角扩径段流出，因此，当钻井液流速0.7 m/s 时，45°斜角扩径段左部堆积的颗粒相比钻井液流速0.6 m/s时所堆积的颗粒明显减少了一半。对于圆弧扩径段，当钻井液流速为0.3 m/s 时，圆弧扩径段的左边堆积了大量颗粒；当钻井液流速0.4 m/s 时，圆弧扩径左部堆积的颗粒大大减少；当钻井液流速为0.5 m/s时，圆弧扩径段处基本无颗粒堆积。

因此，对于直角扩径的钻井液携岩临界流速为0.9 m/s，45°斜角扩径钻井液携岩临界流速为0.7 m/s，圆弧扩径的钻井液携岩临界流速为0.4 m/s。

2.2 不同丰度及颗粒粒径下携岩临界流速图版

将水合物丰度10%、20%、30%条件下对应的含水合物的岩屑颗粒粒径为2 mm、4 mm、6 mm、8 mm 分别进行仿真模拟，其水合物丰度10%、20%、30%条件下对应的颗粒密度分别为2 387.5 kg/m3、2 175 kg/m3、1 962.5 kg/m3，最终得到的 3 种不同扩径方式条件下携岩所需的临界流速图版如图3 所示。

图3 不同水合物丰度不同颗粒粒径携岩临界流速理论图版Fig.3 Theoretical chart of critical flow velocity needed for cuttings carrying under different hydrate abundances and particle sizes

从图3 中可得到：在3 种不同扩径方式下，水合物丰度一定，随着含水合物的岩屑颗粒的增大，携岩所需临界流速增大；含水合物的岩屑颗粒粒径一定，随着水合物丰度的增大，携岩所需临界流速减小。在相同粒径、相同水合物丰度条件下，直角扩径段携岩所需临界流速最大，45°斜角扩径段携岩所需临界流速次之，圆弧扩径段携岩所需临界流速最小。出现这种现象的原因，一是由于水合物丰度的增大使得含水合物的岩屑颗粒的密度减小，扩径段携岩所需临界流速减小；二是由于颗粒粒径的增大，使得颗粒与颗粒之间，颗粒与管壁之间碰撞后再次跳跃能力减弱，且颗粒粒径的增大使得重力增大，钻井液携带含水合物的岩屑颗粒所需的拖拽力增大，所以在扩径段所需临界流速增大。

2.3 不同丰度及钻井液密度下携岩临界流速图版

将水合物丰度为10%、20%、30%条件下对应的钻井液密度为 1 030 kg/m3、1 130 kg/m3、1 230 kg/m3、1 330 kg/m3分别进行仿真模拟，得到3 种扩径方式条件下携岩所需的临界流速图版如图4 所示。

图4 不同水合物丰度不同钻井液密度携岩临界流速理论图版Fig.4 Theoretical chart of critical flow velocity needed for cuttings carrying under different hydrate abundances and drilling fluid densities

从图4 可得到：在3 种不同扩径方式下，水合物丰度一定，随着钻井液密度的增大，携岩所需临界流速减小；钻井液密度一定，随着水合物丰度的增大，携岩所需临界流速减小。在相同钻井液密度、相同水合物丰度条件下，直角扩径段携岩所需临界流速最大，45°斜角扩径段次之，圆弧扩径段最小。出现这种现象的原因，一是由于水合物丰度的增大使得含水合物的岩屑颗粒的密度减小，扩径段携岩所需临界流速减小；二是由于钻井液密度的增大，使得钻井液给含水合物的岩屑颗粒的拖拽力增大，使得扩径段所需临界流速减小。

3 实验模拟验证

3.1 含水合物岩屑颗粒运移模拟实验

在含水合物岩屑颗粒运移模拟实验中，调节泵的排量自0 逐渐增大，实时监测水平管路中固相颗粒运移情况，记录固相颗粒临界起动时的排量，得到不同颗粒粒径下、不同水合物体积分数下的实验数据 (表1)。

表1 不同参数下的含水合物岩屑颗粒运移模拟实验结果Table 1 Result of the simulation experiment on themigration of hydrate bearing cuttings particles at different parameters

颗粒在管路中依次经历了沉积→小颗粒起动→大颗粒起动→大、小颗粒均运移→大量颗粒快速运移几种运动状态。由图5 实验现象可以看出，粒径2 mm 的固相颗粒在排量0.96 L/s(流速0.211 m/s)时临界起动，粒径5 mm 的固相颗粒则需要在排量1.20 L/s(流速0.263 m/s)时才能临界起动，粒径 8 mm 的固相颗粒在排量 1.87 L/s(流速0.410 m/s)时临界起动，粒径10 mm 的固相颗粒在排量1.94 L/s(流速0.425 m/s)时临界起动。

图5 含水合物岩屑颗粒运移模拟实验现象Fig.5 Phenomenon in the simulation experiment on the migration of hydrate bearing cuttings particles

3.2 对比验证

将实验检测的数据与数值仿真结果进行对比，得到不同颗粒粒径下、不同水合物体积分数下的颗粒临界起动流速实验与理论计算值对比曲线(见图6)。

图6 不同条件下颗粒临界起动流速实验值与理论计算值对比曲线Fig.6 Comparison between the measured critical flow velocity needed for particle carrying and the calculation value under different conditions

从图6 可以看出，随着固相粒径的增大，所需临界起动流速增大，其数值仿真结果与实验结果变化趋势一致，且误差为9.62%；随着固相颗粒中水合物体积分数的增大，所需临界起动流速减小，其数值仿真结果与实验结果变化趋势一致，且误差为8.52%。通过数值仿真与实验值的对比，验证了所建立的海洋天然气水合物携岩临界流速理论图版的准确性。

4 结论

(1)建立了直角扩径、45°斜角扩径、圆弧扩径3 种不同扩径方式模型，并用EDEM 和FLUENT 进行耦合仿真，得到携岩所需临界流速理论图版, 为海洋天然气水合物藏水平井开采模式的施工参数优化和井控安全提供了前期技术支撑。

(2)在3 种不同扩径方式下，水合物丰度一定，随着含水合物的岩屑颗粒增大，携岩所需临界流速增大，随着钻井液密度增大，携岩所需临界流速减小；含水合物的岩屑颗粒一定，随着水合物丰度的增大，携岩所需临界流速减小；钻井液密度一定，随着水合物丰度增大，携岩所需临界流速减小。

(3)在同等条件下(岩屑颗粒粒径、水合物丰度及钻井液密度)，直角扩径段携岩所需临界流速最大，45°斜角扩径段所需临界流速次之，圆弧扩径携岩所需临界流速最少。