基于WOA-RVM的滚动轴承退化趋势预测*
2019-11-27范强飞廖爱华丁亚琦
范强飞,廖爱华,丁亚琦
(1.上海工程技术大学 城市轨道交通学院,上海 201620;2.上海地铁维护保障有限公司 车辆分公司,上海 200235)
0 引言
滚动轴承是机械设备的关键部件之一,其性能的退化直接影响设备的运行安全[1]。如果能够尽早预测出滚动轴承性能退化的趋势,在轴承失效前对其进行维修或者更换,对保障设备的安全运行具有重大意义[2-3]。采用有效的预测方法及建立合适的预测模型是滚动轴承性能退化趋势预测需要解决的关键问题。
随着人工智能技术的发展,各种智能预测方法在回归预测领域得到应用。文献[4-5]提出了基于主成分分析法(Principal Component Analysis,PCA)与支持向量机(Support Vector Machine,SVM)相结合的轴承退化趋势预测方法。虽然 SVM 能够实现小样本回归预测,但是核函数参数和惩罚因子的选择会对预测效果产生较大影响。因相关向量机(Relevance Vector Machine,RVM)核函数的选择无需考虑Mercer条件,及其在处理小样本和非线性问题方面具有泛化能力好、预测精度高和鲁棒性强的优点,在趋势预测领域得到一定的应用[6]。在RVM模型预测过程中,模型的预测精度又受到超参数α和核宽度β的影响。文献[7]采用布谷鸟算法(Cuckoo Search,CS)对相关向量机核宽度进行优化,得到了故障预测模型,但算法迭代速度较慢且模型预测精度不高。文献[8]提出利用遗传算法(Genetic Algorithm,GA)来自动确定RVM 的核宽度,但是 GA收敛相对较慢,因遗传、交叉和变异策略选择较为复杂,容易陷入局部最优解。相比于其他优化算法,鲸鱼算法(Whale Optimization Algorithm,WOA)[9]操作简单,容易实现,调整的参数少和跳出局部最优的能力更强。
针对上述问题,本文提出一种基于WOA 优化RVM的预测方法,该方法运用WOA 对RVM 的超参数α和核宽度β寻优。为验证提出方法的有效性,对实测的全寿命滚动轴承的退化趋势进行仿真预测,结果表明建立的基于WOA-RVM的滚动轴承性能退化趋势预测模型,鲁棒性更强,预测精度更高。
1 相关向量机理论
(1)
式中,k(x,xi)为核函数:ω=(ω1,ω2,…,ωM)T为对应权值,N是训练样本总数。
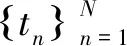
(3)
式中,t=(t1,t2,…,tN)T,Φ=(φ1,φ2,…,φN)T,Φn=(1,k(xn,xi),k(xn,x2),…,k(xn,xN))T。
为实现稀疏化,假设ωn~N(0,1/αi),ω的条件概率分布为:
(4)


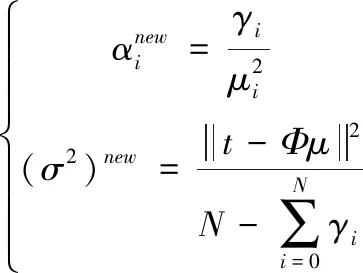
(5)

利用径向基核函数(RBF)作为核函数,即:
(6)
其中,α为核函数宽度。最终得到RVM回归模型为:
(7)
建立RVM输入x=(xn-m,xn-m+1,....,xn-1)与输出y=(xn)一种非线性的映射关系:Rm→R,m为输入维数,然后得到RVM的训练样本和测试样本对为:
(8)
(9)
(10)
(11)
式中,s为训练数据的起点,l是训练样本对数,n为预测点数。RVM的输入为Xtrain,输出为Ytrain,从而训练处预测模型,求出RVM回归估计函数的具体数学表达式。将测试样本Xtest带入式(7)即可得到n个预测值。
2 基于WOA-RVM预测模型的参数优化
2016年,Mirjalili[9]等受座头鲸捕食行为的启发,提出一种结构简单、参数调整少、收敛速度快及全局寻优能力强等特点的群体智能优化算法-WOA。算法主要的迭代过程如下:
Xt+1=Xt-A×D
(12)

A=2a×r-a
(13)
C=2r
(14)
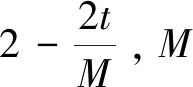

(15)

在这种模型中,更新的鲸鱼个体的位置可以以50%的概率选择收缩包围机制或者选择螺旋式位置更新机制[6]。这种同步行为数学模型描述如下:
(16)
式中,p为[0,1]上的随机数。
当|A|>1时,X=Xrand-A×D
(17)
式中,D=|C×Xrand-X|,Xrand为从当前随机鲸群个体位置。
利用WOA算法优化相关向量机的超参数α和核宽度β,提高模型的预测精度,如图1所示。
算法步骤如下:
步骤1:设置WOA的鲸鱼种群数目sizepop,最大迭代次数maxgen,鲸鱼个体空间维度dim,鲸鱼种群的位置上界ub=[ub1,ub2,...,ubn]和下界lb=[lb1,lb2,...,lbn]。
步骤2:根据本文第二节的方法得到sizepop个鲸鱼个体作为鲸鱼种群的初始位置。
步骤3:WOA算法的适应度函数为均方误差(RMSE),其表达式为:
(18)

步骤4:利用式(18)得到每个鲸鱼群个体适应度值,寻找出目前群体中的最佳鲸鱼个体位置X*,然后将它储存。
步骤5:当t≤maxgen时,更新a、A、C、l和p。
步骤6:当p<0.5时,若|A|<1,通过式(15)更新当前鲸群个体的空间位置;若|A|≥1,则从当前群体中随机选择鲸群个体位置Xrand,并通过式(17)更新当前鲸群个体的空间位置。
步骤7:当p≥0.5时,通过式(16)更新当前鲸群个体的空间位置。
步骤8:通过式(18)计算每个鲸鱼个体的适应度值,寻找出目前群体中的最佳鲸鱼个体位置X*,然后将它储存。然后对鲸鱼优化算法的终止条件进行判定,如果判断为终止,直接步骤9;否则,让t=t+1,对步骤5~8重复执行。
步骤9:输出最优鲸鱼种群个体适应度值所处空间位置X*,X*对应的坐标即是超参数α和核宽度β。

图1 模型参数优化流程
3 滚动轴承实例分析与验证
3.1 实验数据样本来源与预处理
采用来自Cincinnati[11]大学滚动轴承全寿命周期性退化数据来验证所提方法的有效性,其全寿命实验装置及采集仪器布置如图2所示,轴承试验台的转轴上安装了4个Rexnord ZA-2115滚动轴承,每个轴承的X和Y方向各安装一个加速度传感器,采样频率为20kHz,每隔10min采集一次滚动轴承的振动数据,总共采集了984次数据,每次采样长度为20480个点,总共采集了20152320个数据,轴承持续运行了一周,直到失效。根据相关文献[15],滚动轴承在500点之前都是处于正常运行的阶段,退化趋势变化不明显。
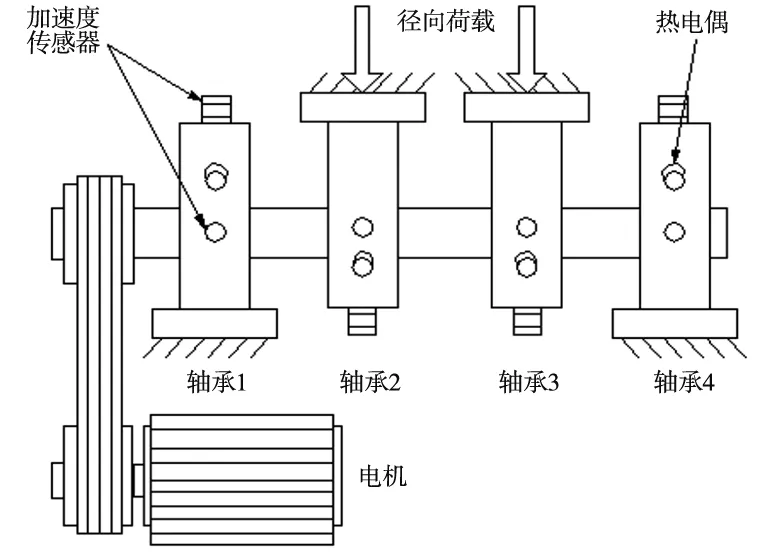
图2 滚动轴承测试装置
由于时域、频域等包含的指标量较多,采用单个指标量无法全面地反映滚动轴承的退化趋势,且单个时域或频域指标还存在评估能力不足的问题[12]。因此,为提取一个能有效地表征滚动轴承退化趋势的特征量,利用PCA融合时域指标和频域指标。提取其第一主成分(PC1)作为滚动轴承的退化趋势性能预测指标,并将其代入基于鲸鱼算法优化的RVM模型中,训练预测模型并完成滚动轴承的趋势预测。
利用PCA融合时域指标和频域指标,提取其第一主成分如图3所示。
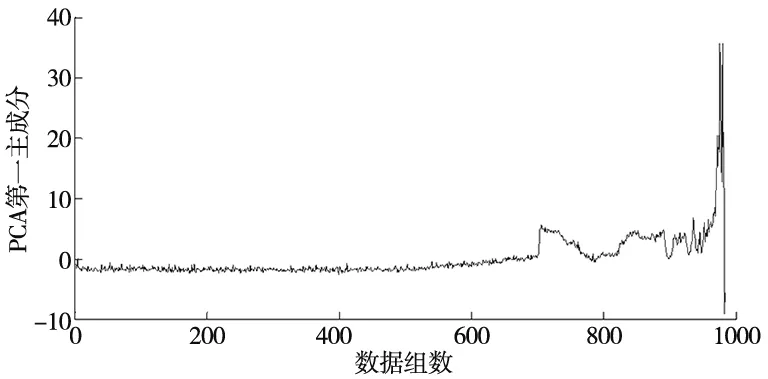
图3 PCA约减融合后的特征指标
由图3可知,选PCA第一主成分(PC1)作为轴承性能退化特征指标时,500点之后有着明显的变化趋势。因此,为了提高运算效率及力求有效表征滚动轴承退化状态,本文选取500至984组数据进行研究。
3.2 滚动轴承性能退化趋势预测
构建好PC1性能退化指标后,将相关向量机的超参数α和核宽度β,通过鲸鱼优化算法来优化。设置鲸鱼种群数目sizepop=30,最大迭代次数maxgen=100,鲸鱼种群空间维度dim=2。为了准确的评价预测结果,利用平均绝对百分比误差作为预测效果的评价指标[9],即:
(19)
在预测模型确定情况下,将得到的预测数据作为下一步预测的输入,循环迭代实现预测[13]。由式(8)~式(11)建立预测模型,利用500点之后的数据进行训练和预测,预测起始点s=500,训练样本对数l=133,输入向量维数m=20,预测步数n=20。利用本文1.3节的参数优化方法得到超参数α=0.816和核宽度β=1.512,并构建相关向量机模型。图4为3种方法的收敛趋势图。由图4可见,WOA收敛速度最快,在第33代时出现最优适应度值,对应的最低均方误差是0.08。与其他两种算法相比较,WOA不仅收敛速度最快,收敛精度也是最低。
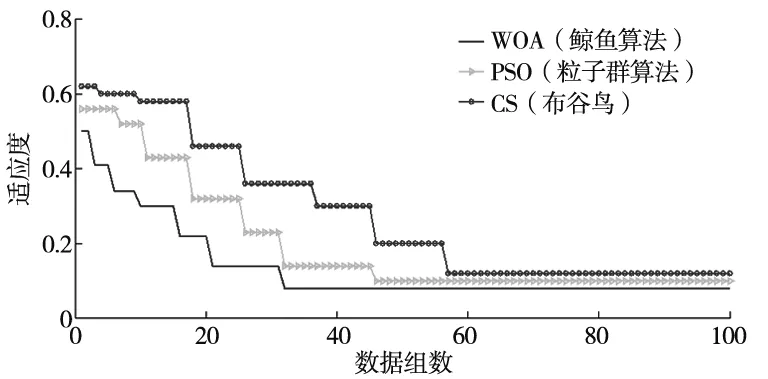
图4 3种方法寻优RVM参数的适应度值收敛趋势图
利用PC1作为特征指标,对测试样本利用5种预测方法(①WOA算法优化RVM模型;②WOA算法优化SVM模型;③PSO算法优化RVM模型;④布谷鸟算法优化RVM模型;⑤RVM)进行退化趋势预测的预测曲线与实际状态趋势比较如图5所示。

图5 滚动轴承趋势预测曲线与实际状态趋势
在20步的预测范围内,测试样本各模型预测的误差曲线如图6所示。

图6 测试样本各模型预测的误差曲线图
5种方法预测结果与真实值之间的误差比较如表1所示,其中MAPE表示平均绝对百分比误差,RMSE表示均方根误差,MAE表示平均绝对误差。

表1 5种方法预测结果误差比较
从图5和表1可以看出,采用PCA融合后的第一主成分作为性能退化指标,综合比较,基于WOA-RVM预测的曲线更接近于真实值,其MAPE、RMSE、MAE较其他4种预测方法的误差也低很多。基于WOA-RVM预测的RMSE仅为0.0801,与其他预测模型的RMSE值相比,也为最小,这是因为WOA结构较为简单,需要调整的参数较少。另外,由图6可以看出,基于WOA-RVM的预测误差曲线较其他4种预测方法,波动更小,整体更加平稳。因此基于WOA-RVM预测模型的预测误差相对较低,能更加精确预测滚动轴承的退化趋势。
在实际工程应用中,首先训练好一个轴承预测模型,然后通过已经训练好的模型对与其具有相同工况和相同型号的轴承进行性能退化趋势预测。从图2可知,轴承2和轴承3具有类似的工况和相同型号,所以用事先训练的轴承2预测模型预测轴承3的性能退化趋势,轴承3的性能退化趋势预测结果如图7所示,测试样本各模型预测的误差曲线如图8所示。
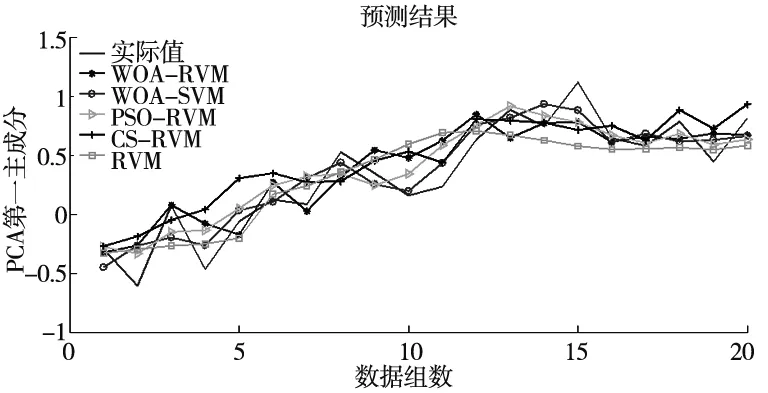
图7 滚动轴承趋势预测曲线与实际状态趋势图

图8 测试样本各模型预测的误差曲线图
5种方法预测结果与真实值之间的误差比较如表2所示。

表2 5种方法预测结果误差比较
通过图7、图8和表2可以得到,利用PCA融合后的第一主成分作为性能退化指标,用轴承2训练模型预测轴承3的性能退化趋势,基于WOA-RVM预测模型的综合预测误差最小。
4 结论
针对RVM,在滚动轴承性能退化趋势预测中,呈现的参数选择盲目问题,本文提出了一种基于WOA优化的RVM预测方法,重点研究了WOA对RVM在核函数参数选择方面的优化过程,使得RVM的超参数α及核宽度β更加精确。通过滚动轴承全寿命振动数据的预测对比分析,计算结果表明利用PCA融合后的第一主成分作为性能退化指标,与基于WOA-SVM模型、PSO-RVM模型、CS-RVM模型及RVM文中所提四种预测方法比较,基于WOA优化的RVM预测模型的预测误差更小,精度更高。
WOA是一种调整参数少、收敛速度快的全局寻优能力强的群体智能优化算法,将其与RVM相结合,优化RVM的预测过程,为滚动轴承退化趋势预测提供了一种新方法。
