基于扩展有限元的薄板裂纹损伤分析*
2019-11-27蒋占四谢凤乐宋威震
余 鼐,蒋占四,谢凤乐,徐 飞,宋威震
(桂林电子科技大学 机械工程学院, 广西 桂林 541000)
0 引言
板类结构被广泛地应用,如火箭尾翼、太阳能板等。如果这些机体中的板存在裂纹,会使装备在服役过程中因裂纹的扩展形成断裂或者变形,使机体的强度与振动特性等方面发生变化,从而影响机体的使用性能,甚至产生重大的事故。而早期初始裂纹源比较小且受工作环境的影响不易被发现 ,因此监测并预示早期裂纹发生的位置与深度是损伤识别领域的一个重要研究方向[1]。
板的裂纹识别,从原理上讲,与其他传统检测方式类似。首先由探头测量出缺陷对外界激励的响应, 再使用适当的方法作识别分析[1]。不同于传统的检测方式,在得到外界的激励响应后,建立裂纹板的数值分析模型,在模型上结合算法反演推算出裂纹的参数信息是一种新的检测方式。1999年,美国西北大学的学者提出了一种用最小重构网格的有限单元法模拟弹性裂纹扩展[2];随后采用阶跃函数加强裂纹贯穿单元,用裂尖函数加强裂尖单元,进一步完善了该数值分析方法[3]。
在国内外已有研究中,Krawczuk等通过特殊谱单元分析确定裂纹的位置[4]。Horibe和Watanabe应用遗传算法来识别裂纹的位置[5],但以上方法都只能寻优平行于板边界的裂纹;ChatziE N,用扩展有限元法采用椭圆形孔洞模拟出了静态薄板在受拉状态下任意形状的缺陷,反问题用的是遗传算法进行寻优[6]。这一改进虽然能够不再局限于平行裂纹,但该算法效率低且在反问题寻优中容易陷入局部最优解。Rabinovich D,基于扩展有限元法和遗传算法识别出了静、动载下平板薄膜内部的裂纹[7-8];江守燕[9]给出了用扩展有限元结合蜂群算法求解任意裂纹的策略;王珍兰等[10]提出了一种改进的蜂群算法,改善了反演过程中局部最优解的情况。但算法的改进较复杂,且寻多变量问题耗时很长。
本文通过结合扩展有限元法与粒子群算法。首先用水平集法模拟裂纹位置并引入模拟裂纹不连续面的加强函数,建立板类结构正问题分析模型,避免了网格重划分和网格细化带来的影响。在此基础上用近似模型(RBF)代替原有的结构参数与动力响应关系,最大程度降低正问题中的计算量。反问题中粒子群算法反演寻优求解出与输入值相差最小的样本点从而定量预测出裂纹的相关参数,并讨论了不同边界条件对模型准确性带来的影响。
1 扩展有限元建模
扩展有限元的基本原理也是基于单位分解的思想。只是在处理一些强,弱不连续问题中,它用一些加强函数反映间断特性。而没有间断部分依然采用有限元处理。
1.1 单元的选择
等参单元,即单元坐标变换和位移函数采用相同的插值形函数。选用等参单元能很好的适应非正交的直线边界,单元大小也方便调节。单元的位移模式一般如下:
(1)
其中形函数为:
(2)
式中,ξ、η为该四边形单元的局部坐标,ξi、ηi为4个角节点的局部坐标值,其取值如下:
(3)
1.2 含裂纹单元的处理
裂纹作为一种强不连续问题,位移模式中为了反映不连续性的存在,需要在裂纹单元形函数中增加与内部的几何或物理界面有关的加强函数。裂纹单元由裂尖单元和裂纹贯穿单元组成。裂纹贯穿单元两侧位移的特征是不连续,因此整体加强函数只要能反映裂纹两侧位移的不连续即可,一般选取阶跃函数H(X)[3]进行加强:
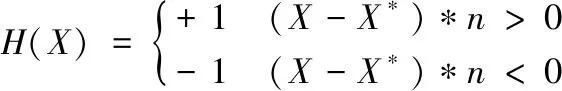
(4)
式中,X*是考察点X在裂纹面上的投影点;n为裂纹面的单位外法向。
含裂尖单元的整体加强函数要能够反映裂尖主要的奇异项和各种可能的位移状态。通过裂尖改进函数Fj(X)[3]进行表示:
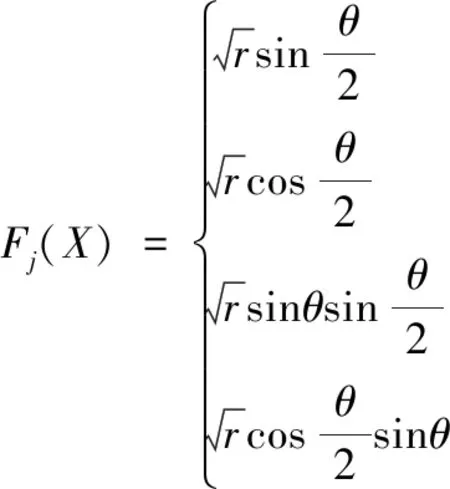
(5)
其中,r和θ为裂尖局部极坐标。
1.3 裂纹的定位
建模过程分析的裂纹不止一条,裂纹的定位采用水平集函数。水平集函数由正交的符号距离函数Ψ(x,t)和波前水平集φk(x,t) (k=1,2)组成。Ψ(x,t)的零水平集Ψ(x,t)=0表示裂纹面,表达式[11]如下:
(6)
式中,x为考察点p的坐标;x*为考察点p在裂纹面上的投影点坐标;n为裂纹面的单位外法向。
sign(x)为符号函数:

(7)
波前水平集函数:
φk(x,t)=(x-xk)·t
(8)
xk为第k个裂尖坐标;t为第k个裂纹尖端处的单位切向矢量。
1.4 扩展有限元位移模式
(9)

2 反问题求解与近似模型
2.1 反问题分析
在反问题中,缺陷对外界激励的响应是已知的。即可以在板的边缘设计一些方便测量的点,用传感器接收数据,得到结构在这些测量点的位移或者是应力,所得到的结果称为实际测量结果。在此基础上反问题的目的就是凭借实际测量结果尽可能定量诊断出裂纹的损伤情况(位置,形状等)。
反问题分析过程中在描述单个裂纹时,参数用如下向量表示:
δi=(X1,Y1,X2,Y2)
(10)
其中,(X1,Y1)表示的是裂纹起点坐标;(X2,Y2)表示的是裂纹终点坐标。
为准确定位裂纹的损伤情况,通常需要结合一些优化算法(粒子群算法)在正问题扩展有限元模型中计算出结构关键点的响应,并与实际测量结果进行比较,使得二者之间误差即目标函数最小化。从而实现定量预测裂纹位置。
其目标函数[6]可设为:
(11)
本文用的粒子群算法(PSO)属于智能算法的一种,是通过模拟鸟群捕食行为设计的。假设区域里就只有一块食物,鸟群的任务是找到这个食物源,群体中的每个成员通过学习它自身的经验和其他成员的经验来不断改变其搜索模式。其一般参数如下:
(1)初始粒子数25;
(2)粒子的寻优范围(-0.5,0.5);
(3)粒子速度的最大值Vmax设置为0.1,即最大寻优范围的0.1;
(4)加速系数C1,C2设置为2;
(5)随机数r1,r2设置为[0,1]。
2.2 近似模型的引入
在模型生成之后,直接寻优容易陷入局部最优解,有时需要建立与裂纹参数相对应的响应数据库。而每生成数据库中的一个数据点,都要计算一次该状态下的位移。这样不仅非常耗时,而且不利于实际工程应用。因此本文在此基础上引入径向基(RBF)代理模型,减少建模过程中的计算量,其流程图如图1所示。
RBF代理模型[12]是通过用样本点的输入和输出信息,来模拟源模型中目标函数和设计变量之间的关系,从而替代复杂的源模型进行计算。RBF 模型可表示为:
(12)
其中,N是插值样本点的个数,φ是径向距离。

Aλ=f
(13)
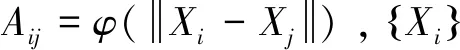
3 数值算例
如图2所示,含裂纹的方形板,板长W和宽L都为1m。在数值计算时,假设板处于平面应力状态。板的下端施加合适的约束条件消除刚体位移,上端受水平向拉伸(切向)荷载σ=1.0 MPa 的作用;板的弹性模量为E=2E11Pa,泊松比ν=0.3。本次边界条件分两种情况进行讨论,板被离散成41×31的等参单元网格。在板四周合适的位置布置有参数点,用以方便通过传感器测得该处结构的真实响应。

(a) 边界受拉力 (b) 边界受切向力 图2 几何尺寸及载荷分布图
为了验证此次建模的正确性,取工况一为研究对象,将正问题扩展有限元建模所得的数据与商业ANSYS的有限元计算结果进行比较,如图3所示。

(a) 有限元计算结果 (b) 扩展有限元计算结果 图3 中心裂纹板的扩展有限元模型
从图3可以看出,裂纹在受力作用后的张开程度和位移变化点基本吻合,从而验证了所用扩展有限元数据的正确性。
按照裂纹识别步骤用扩展有限元计算出拉丁超立方抽样的20组裂纹参数(位置坐标)对应的位移,以此建立初始RBF模型。粒子群法参数设置如上。裂纹板上有8种位置工况 A~H ,识别结果如表1、表2所示。从表1薄板在受拉下和表2薄板在切向力作用下的结果可以看出,在8种工况中,即使边界条件不一样,识别的结果也与真实裂纹参数十分接近,基本上在2%之内。可以准确地描述裂纹位置与结构的位移之间的关系。

表1 薄板受拉情况下裂纹真实值与识别结果比较

表2 薄板受切向力情况下裂纹真实值与识别结果比较
4 结论
(1)通过等参单元划分单元网格,并用水平集法确定单元类型,从而引入加强函数对裂纹单元进行改进,建立了损伤薄板的扩展有限元模型。简化了损伤薄板仿真的步骤。
(2)反问题中不需对算法进行太大改进。引入近似模型代替原有结构的静力学输入、输出关系,在很大程度上避免了正问题优化迭代过程,适合工程应用。且仿真结果表明:所建立的反演结构能够准确地识别出结构内部单个缺陷的位置和大小。
