海洋工程数值风-浪-流水池模拟及分析*
2019-11-27刘红兵陈国明
刘红兵 陈国明 吕 涛 黄 翱
(1. 中国石油大学(华东)海洋油气装备与安全技术研究中心 山东青岛 266580; 2. 哈尔滨工程大学船舶工程学院 黑龙江哈尔滨 150001)
在复杂的海洋环境中,风、浪、流通常是共同存在且相互交替运动,从而产生类似于“Doppler”效应的风-浪-流耦合作用[1],导致流场结构和波浪幅值、波高、周期等波浪要素发生改变,使得波浪发生折射乃至破碎[2]。因此,准确模拟海洋风-浪-流时空分布特征,探讨风-浪-流耦合作用机理以及耦合作用下风-浪-流场分布特征,对于保证海洋工程结构物安全运行具有重要意义[3]。
目前,国内外关于海洋环境水动力性能的研究主要采用理论研究、实尺试验、模型试验和数值水池模拟等方法。基于无黏无旋假设的势流理论可以快速计算波浪传播及其对海洋工程结构物的作用,却无法计算由于黏性效应引起的一些物理现象,如风-浪-流耦合远程传播和漩涡演变等,具有较大的局限性[4]。实尺试验法受海洋环境影响因素较大,且试验成本高并难以控制,在海洋工程应用中难以实现[5]。模型试验法主要采用一定的缩尺比例转化关系,通过缩尺模型水动力学性能反映整体结构水动力学性能,在海洋工程中应用较为广泛,但存在试验成本高、试验周期长、试验缩尺模型和原型之间准确转换困难等缺陷,使其应用仍受到一定限制[6]。随着近年计算机技术高速发展,数值波浪水池以其低成本、短周期和高精度等特点,在海洋工程波浪诱导运动和波浪载荷预测等方面得到了广泛应用[7]。例如,Wang[8]和苏晓杰 等[9]基于欧拉-拉格朗日算法追踪流体瞬时自由液面的变化过程,建立了完全非线性的三维数值波浪水池。Alamian等[10]利用活塞运动造波法,在数值波浪水池中模拟了线性波和非线性波;Finnegan等[11]基于CFX软件,建立了摇板式数值波浪水池;梁修峰 等[12]基于FLUENT软件建立了一种面向海洋工程应用的二维数值波浪水池,并对非线性Jonswap波浪谱进行了模拟。但这些数值水池研究主要集中于单一波浪运动规律的研究,而对于风-浪-流三者之间相互耦合作用研究较少。本文基于FLUENT软件,利用UDF二次开发,构建了一种适于三维海洋工程的数值风-浪-流水池,成功模拟了风-浪-流之间的相互耦合作用,并探讨了风和海流对波浪的影响。
1 数值风-浪-流水池数学模型
1.1 控制方程
假定数值风-浪-流水池所涉及的流体(空气和海水)均为不可压缩黏性流体,则数值风-浪-流水池连续性方程和动量方程分别为
(1)
(2)

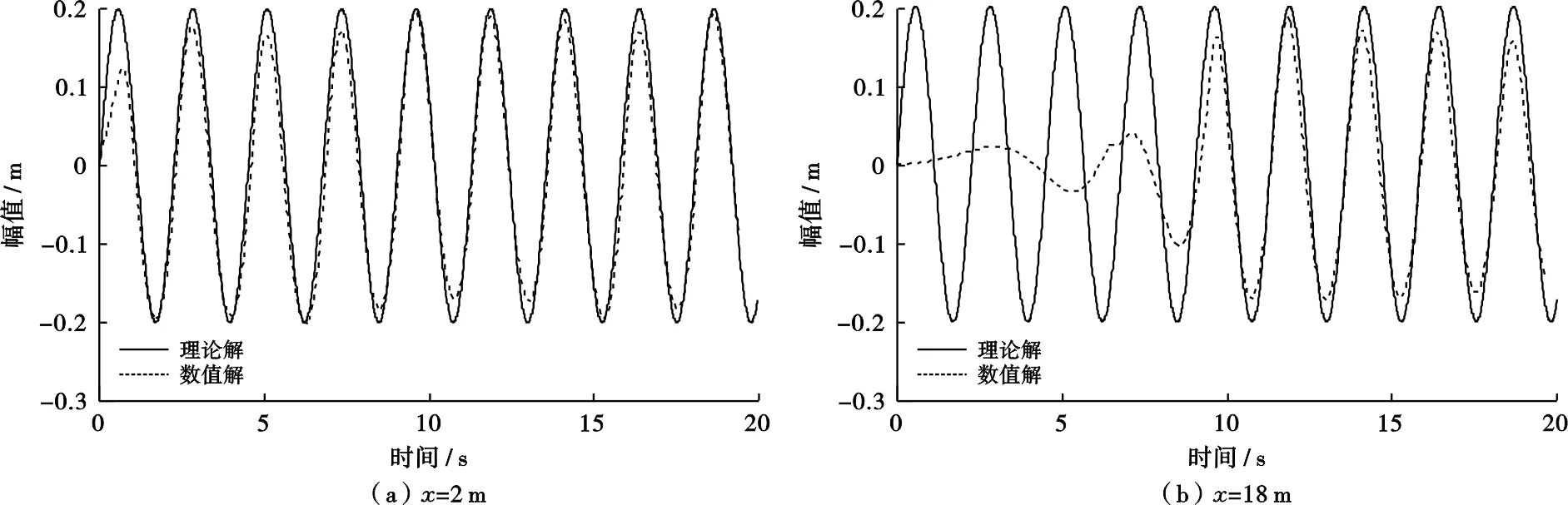
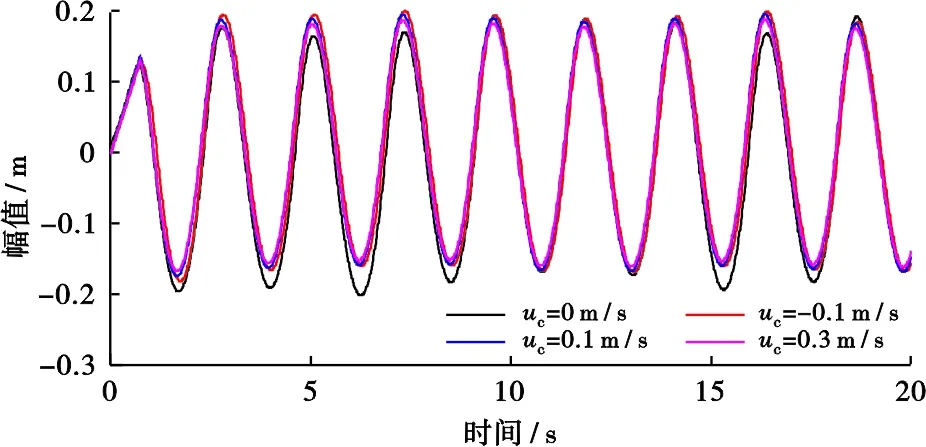
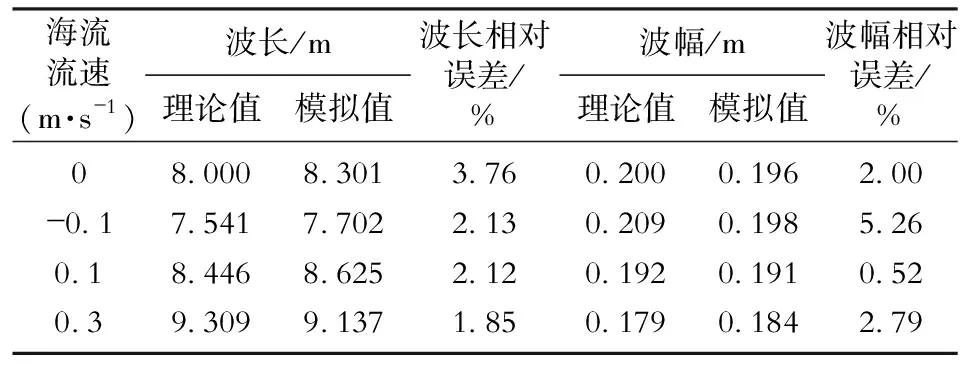
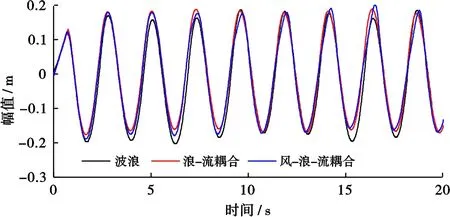
波浪传播过程中,其气-液交界面时刻发生改变,因而需要准确追踪自由液面。本文采用VOF方法捕捉自由液面,即通过引入单元内各流体体积分数aq来捕捉气液两相自由液面。当aq=0时,表示该网格单元内没有q相流体;当aq=1时,表示该网格单元内充满q相流体;当0 (3) 式(3)中:aq为q相流体在网格内所占体积分数,当q=1、2时,aq分别表示空气、水相体积分数。 数值造波方法对于数值水池准确模拟波浪传播特性具有重要作用,现阶段主要的数值造波方法有仿物理造波法(推板造波法和摇板造波法)[13]、边界造波法[14]和源项造波法[15]等,其中仿物理造波法原理简单,造波功能完善,但对计算区域内网格质量要求较高,计算时间长;源项造波法产生的波浪效果好,波形稳定,但计算量大,且不易收敛;边界造波法通过在波浪入射边界给定波浪水质点速度和波面高度,从而生成数值波浪,具有较好的适用性并在海洋工程波浪领域应用较为广泛。因此,采用边界造波法将风-浪-流水池入口设置为风-浪-流相互作用的起始位置,各速度场方程可由Airy线性波浪和梯度风场理论描述,其中波面方程为 (4) 式(4)中:η为波面高度,m;H为波高,m;k为在2π相位角内波的个数,rad/m;w为2π相位角内波的振动次数,rad/s;x为X方向位移,m。 风-浪-流水池入口速度包括自由液面以下水质点运动速度和自由液面以上空气运动速度,其中入口水质点速度由波浪水质点速度和水流流动速度两部分组成,可根据波流共同作用下流速场理论进行叠加[16],即 ux=uwx+uc= (5) (6) 式(5)、(6)中:ux、uz分别为水质点X和Z方向速度,m/s;uwx为波浪水质点速度,m/s;z表示Z方向上的位移,m;uc为水流速度,m/s;T为波浪周期,s;d为水深,m。 自由液面之上的空气流动速度可采用指数梯度风进行定义[9],即 (7) 采用数值风-浪-流水池进行模拟时,当波浪传播至水池末端时,波浪会产生反射,对前进波浪产生干扰。因此,为准确获得高质量、高精度的波浪,需对反射波进行消波处理。常用的消波方法主要有多孔介质消波法和动量阻尼消波法,其中多孔介质消波法通过在消波段设置一个多孔介质区域,实现消波目的,但关于多孔介质模型的选取及参数的设置较为复杂;动量阻尼消波法通过在消波段的流体动量方程中添加一个黏性阻尼衰减项,从而实现消波目的。消波段动量方程[10]为 (8) (9) 式(8)、(9)中:θ为动量阻尼消波系数;x0和x1分别为消波段前端和尾端X方向坐标,m;θ1为动量阻尼消波经验系数,取值10。 采用GAMBIT建立三维数值风-浪-流水池几何模型并划分网格,其整体尺寸为:长50 m、宽20 m、高15 m、水深为10 m、右端消波段长度为8 m,如图1所示。整个数值风-浪-流水池网格采用渐进式六面体网格,越靠近水池底端、右端和上端边界处网格越稀疏,同时对自由液面附近两倍波高区域进行加密处理,便于更好地捕捉波形变化。 图1 数值风-浪-流水池几何模型网格划分 数值风-浪-流水池左边界设置为速度入口,气液两相速度值和体积组分数可根据气液两相运动速度场和波面运动方程并采用UDF进行定义;右边界设置为自由出流边界,上边界设置为对称边界,其余边界为固壁边界。造波过程中,采用三维非定常分离隐式求解器求解,其中湍流模型为RNGk-ε模型,压力速度之间的耦合作用采用PISO算法,离散格式为中心差分格式,压力方程采用加权体积力格式,动量方程、湍动能和湍动能耗散率方程均采用二阶迎风格式。压力参考值为一个标准大气压,重力加速度为-9.81 m/s2,时间步长为0.01 s。 为了验证数值风-浪-流水池的准确性和适用性,采用线性Airy波浪对其进行验证。设定模拟的线性Airy波浪参数为:波长L=8 m,波高H=0.40 m,波陡λ=0.05,周期T=2.263 6 s,波速c=3.534 2 m/s。图2为该线性Airy波浪生成和传播过程示意图,上部蓝色部分为空气,下部红色部分为水,中间绿色部分为波面,可以看出t=20 s时数值水池已形成稳定的Airy波面,同时水池右端采用动量阻尼消波效果较好,消波段波面基本保持不变。 图2 Airy波浪生成和传播过程 分别在数值风-浪-流水池中不同位置处设置浪高仪,实时监测不同位置处波面时程。x=2 m和x=18 m位置处波面时程如图3所示,可以看出,两个位置处波面时程均较为稳定,且与理论波面时程变化规律基本一致,其中x=2 m处数值波面时程与理论波面时程吻合度较高,而x=18 m处数值波面时程峰值略小于理论波面峰值,这主要是由于波浪传播过程中由于黏滞耗能等影响而导致波浪最大幅值呈现一定程度的衰减。 图3 波浪数值波形和理论波形比较 进一步统计该数值模拟波浪的波长、波幅和周期等特征,并与理论值进行比较分析(表1),可以看出:数值波长平均值为8.301 m,与理论波长相对误差(取绝对值,余同)为3.76%;x=2 m处,模拟波幅为0.196 m,与理论波幅相对误差为2.00%;随着x取值逐渐远离造波边界,模拟波幅与理论波幅相对误差绝对值逐渐增大,这主要是由于波浪传播过程中会存在逐步的衰减作用,但波幅相对误差均小于10%,且不同位置处波浪周期与理论周期相对误差均小于1%,充分验证了该数值风-浪-流水池模拟波浪的可靠性。 表1 波长、波幅和周期模拟值与理论值相对误差统计 根据式(5)~(10),分别设定浪-流耦合作用下造波和消波方法,其中速度入口边界通过UDF进行定义(包括流速场和风场),消波段通过增加UDF添加动量阻尼源项进行消波,然后利用数值风-浪-流水池模拟浪-流耦合作用。为了便于比较,设定浪-流耦合作用几何模型、边界条件、物理属性以及波浪参数等均与模型验证时保持一致;海流速度共设置4组,分别为uc=0 、-0.1 、 0.1 、0.3 m/s。 图4为4种不同海流流速下x=2 m处波面时程曲线,可以看出,不同流速下波面时程曲线形状基本保持一致,但流速越大波面时程形成稳定波形所需时间越短,即uc=0.3 m/s时波形最先达到稳定,uc=-0.1 m/s时波浪最后达到稳定状态。这主要是由于波流同向时,海流对波浪传播具有推动作用,导致波浪传播速度加快;而波流逆向时,海流对波浪传播具有阻碍作用。 图4 浪-流耦合作用下x=2 m处波面时程对比 分别提取4种不同流速下的波长和波幅,并同波流耦合作用下波长和波幅理论计算公式[16]进行比较分析,结果见表2。由表2知,4种流速下数值波长和波幅与理论值吻合较好,其中数值波长和理论波长最大相对误差为3.76%,数值波幅和理论波幅最大相对误差为5.35%。对比4种流速下波浪峰值大小可知,uc=-0.1 m/s时波浪峰值最大,uc=0.3 m/s时波浪峰值最小,这主要是由于波流同向时,波浪传播速度增大,波形被拉长,导致波浪峰值减小;而波流逆向时,波浪传播速度减小,波形被压缩,导致波浪峰值增大所致。 表2 浪-流耦合作用下波长和波幅模拟值与理论值 实际海洋环境中通常风、浪、流三者是共同存在的,进一步基于该数值风-浪-流水池模拟风-浪-流耦合作用。根据式(7)在造波边界自由液面上方空气区域施加梯度风风场,同时海流速度uc取值0.1 m/s,波浪及其他物理参数与上述完全相同。图5为考虑波浪、浪-流耦合以及风-浪-流耦合等3种情况下,x=2 m位置处波面时程对比,可以看出,风-浪-流耦合作用下波面达到稳定时间和浪-流耦合作用下达到稳定时间差不多,但比单纯波浪达到稳定时间快;风-浪-流耦合作用下波面峰值附近呈现一定的倾角,这主要是由于海风使得波面峰值附近波浪运动速度加快,导致波峰发生倾斜,加速波浪发生碎浪现象。进一步统计风-浪-流耦合作用下波浪波长和波幅,其平均值分别为8.836 m和0.185 m,相比于浪-流耦合作用下的波长和波幅分别增大2.45%和减小3.14%。 图5 风-浪-流耦合作用下x=2 m处波面时程对比 1) 基于FLUENT软件,通过UDF二次开发,构建了适于海洋工程的数值风-浪-流水池,实现了数值风-浪-流水池造波和消波功能,成功模拟了浪-流以及风-浪-流相互耦合作用,模拟结果与理论结果吻合度较好,验证了该数值风-浪-流水池具有较好的精度。 2) 浪-流耦合作用数值模拟结果表明,海流对于波浪运动参数具有较大影响。波流同向时,海流导致波浪传播速度和波长增大,幅值减小;波流逆向时,波浪传播速度和波长均减小,波幅增大,且海流速度越大,波浪参数增大或减小的幅度越明显。 3) 风-浪-流耦合作用数值模拟结果表明,风会导致波浪传播过程中波长增大,波幅减小,同时会导致波峰呈现一定倾角,加速波浪发生破碎。1.2 造波方法
1.3 消波方法
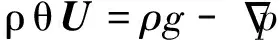
2 数值风-浪-流水池模拟及分析
2.1 网格模型及参数设置

2.2 模型验证


2.3 浪-流耦合作用模拟及分析
2.4 风-浪-流耦合作用模拟及分析
3 结论
