二维保修装备可用度优化模型
2019-11-27程中华白永生赵汝东郭尚昆
程中华, 王 谦,2, 白永生, 赵汝东, 郭尚昆
(1. 陆军工程大学石家庄校区装备指挥与管理系, 河北 石家庄 050003; 2. 陆军第九综合训练基地教研部,河北 张家口 075000)
当前,在装备保修服务中,一般通过实施预防性维修来提高装备保修期内的可用度和部队的满意度。因为通过预防性维修可降低装备发生故障的概率,提高装备性能,达到减少保修期内装备故障次数、缩短停机时间、提高可用度的目的。目前,诸多学者均对预防性维修进行了研究报道[1-3]。相对而言,一维保修期内的预防性维修研究成果较多,二维保修期内的预防性维修研究成果相对较少,且多数研究是从装备保修合同商的角度进行分析,对保修费用的相关研究较多,而对装备使用方关注的可用度研究不足。二维保修是指同时采用使用时间和使用程度2个维度来决定保修终止期限的保修服务。二维保修装备具有随2个维度同时退化的特性。在装备使用过程中,当达到任一维度的阈值时,保修服务都将终止。如:某军用车辆的保修期为3 a、5×104km,即当使用时间达到3 a或行驶里程达到5×104km,保修服务均将结束。
二维保修装备具有结构复杂、维修难度大等特点。保修期内通常不轻易更换整个装备,只进行局部的维修或保养,可在一定程度上降低装备故障率。为了满足日常维修保养的需要,通常要求装备所在部队具备一定的维修保障能力,预防性维修工作通常由部队自身来完成。但针对在保修期内的二维保修装备,部队很难快速形成较高的维修能力,与装备生产厂家相比,对装备的维修效果还存在一定的差距。因此,在二维保修期内,若只由部队实施预防性维修,可能会存在装备故障率恢复程度不高、故障频发、停机时间长等问题。
按照预防性维修对装备故障率λ的恢复程度,通常将预防性维修程度分为最小预防性维修、不完全预防性维修和完全预防性维修3种,并采用修复因子δ(0≤δ≤1)来表示不同维修程度对装备故障率恢复程度的影响。在最小预防性维修情况下,维修后仅仅使装备恢复到维修之前的水平(修复如旧),则修复因子δ=1。在完全预防性维修情况下,维修后可使装备恢复到如同新品一样(修复如新),则修复因子δ=0。在不完全预防性维修情况下,装备恢复情况介于修复如新和修复如旧之间[4],则修复因子0<δ<1。假设在时刻T对装备进行了不同程度的维修,其对装备故障率的影响如图1所示。

图1 不同维修程度对装备故障率的影响
对于大型的军用装备,通常实施不完全预防性维修,因此不可能通过预防性维修使装备恢复到与新装备一样。研究表明[5]:通过维修可以将装备当前时刻的故障率降低到实际使用工龄前某一工龄的故障率,则之前的这一时刻称为虚拟工龄。如:某汽车在使用100 d后,厂家对其进行了1次不完全预防性维修,维修后的汽车故障率恢复到与使用了80 d时的故障率一样,则80 d为其虚拟工龄。通过对装备实施不完全预防性维修,可假设按照一定比例缩减了此次维修之前的虚拟工龄,通常采用比例年龄倒退模型来表示不完全预防性维修对装备虚拟工龄的影响[6-8]。不完全预防性维修对装备虚拟工龄的影响程度不同,维修程度越高,维修所需时间越长,这与维修的实际情况相符。如:某军用装备若由厂家实施不完全预防性维修后,其虚拟工龄要比由部队实施后的虚拟工龄更短。因此,对于这类二维保修装备,笔者提出了新的保修策略:在保修期内,由厂家和部队分别对装备实施预防性维修,且厂家实施预防性维修的维修程度高于部队的维修程度。
但在当前有关保修策略的文献报道中,所实施的预防性维修多是单一维修程度,在进行预防性维修间隔期决策时鲜有相关模型可以借鉴。如:WANG等[9]从制造商的角度提出了对保修装备实施周期性不完全预防性维修,研究不同使用率下装备的最优保修策略;HUANG等[10]假设在保修期内实施不完全预防性维修,建立了保修费用模型,并给出最优保修方案;PARK等[3]提出在保修期内执行维修程度恒定的不完全预防性维修,对预防性维修期间的故障进行最小预防性维修或更换维修,确定了使保修成本最低的预防性维修间隔期;仅有LIAO[11]提到了将保修期内的预防性维修分为完全维修、不完全维修和预测性维修3种类型。且目前文献报道的保修策略中预防性维修很少包涵2种或2种以上的维修程度。而这样的保修策略,在二维保修服务中会有很大的应用价值。本文提出保修期内厂家和部队分别对装备实施不同维修程度的不完全预防性维修,并建立装备可用度模型。
1 二维保修可用度模型
1.1 问题描述
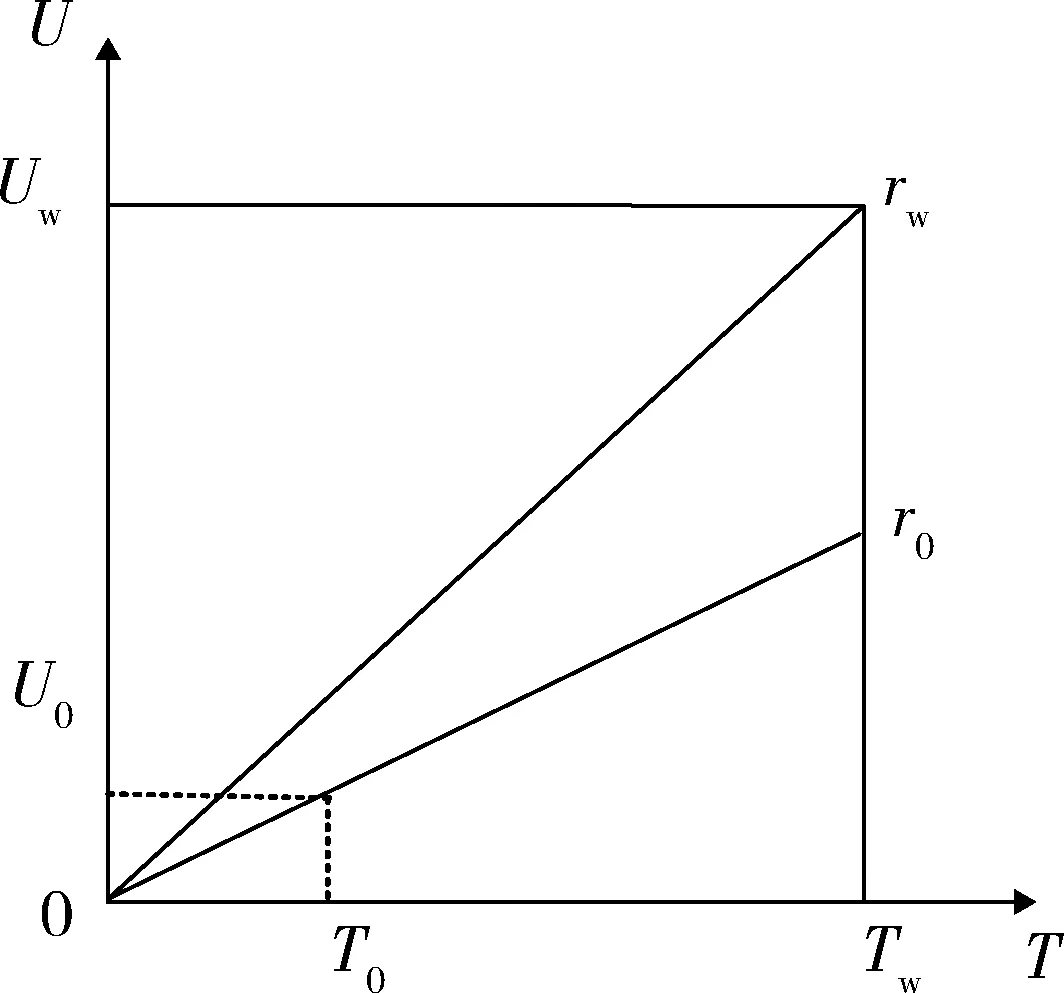
设Tw、Uw分别为保修时间期限和使用度期限,(Tw,Uw)为装备的二维保修期,rw=Uw/Tw,为装备的设计使用率。保修期内以间隔期(T0,U0)实施周期性的不完全预防性维修,T0和U0分别为预防性维修的时间间隔期和使用度间隔期,即每当装备使用时间间隔达到T0或使用程度间隔达到U0,就实施1次预防性维修,r0=U0/T0。实施预防性维修后,装备的虚拟工龄会降低。当装备出现故障后,由厂家负责维修,维修程度为最小预防性维修,由最小预防性维修导致的平均停机时间为TF。目前二维保修装备的故障率表示方法主要有双因素变量法、复合尺度法和使用率法3种,其中,使用率法应用比较广泛,笔者采用该种表示方法。对于某一给定的用户,假设装备使用率r为定值[12-13],则装备故障率[14]
λ(t|r)=θ0+θ1r+θ2t2+θ3rt2,
(1)
式中:参数θ0、θ1、θ2、θ3的值可根据装备历史故障数据估算得到。但是,不同用户其装备的使用率不同。对于批次装备而言,不同用户的装备使用率为服从某一分布的随机变量。假设G(r)、g(r)分别为装备使用率的分布函数和概率密度函数,装备使用率服从双参数威布尔分布,其概率密度函数为
g(r)=(β/α)×(r/α)β-1×e-(r/α)β,
(2)
式中:α为尺度参数;β为形状参数。
当采用厂家和部队分别实施预防性维修保修策略时,保修期内共执行Nw次预防性维修。为研究方便,笔者仅讨论厂家实施1次预防性维修的情况,且假设厂家实施预防性维修后对装备故障率的恢复效果更好。设m为不完全维修程度,其与修复因子的关系为[15-16]
δ(m)=(1+m)e-m,
(3)
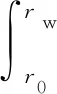
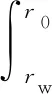
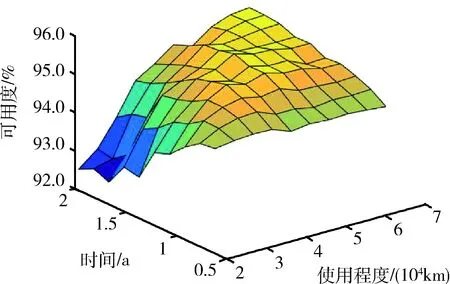
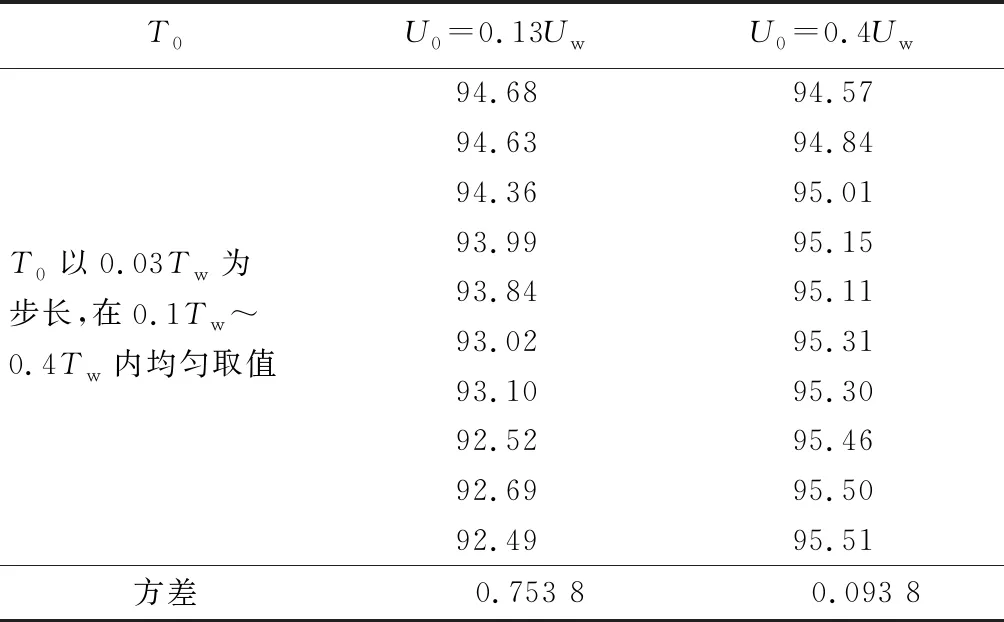
m1和m2(m1 T+=δ(m)×T-, (4) 相应的故障率 λ(T+)=λ(δ(m)×T-)。 (5) 在Nw次预防性维修中,假设第N(N∈[1,Nw])次维修由厂家实施,剩余Nw-1次全部由部队实施。当厂家预防性维修的时机N发生变化时,装备故障率的变化趋势也随之改变,进而影响保修期内故障发生的次数和停机时间。在保修期内,装备停机时间由预防性维修造成的停机时间和修复性维修造成的停机时间2部分组成。 设λk(t|r)为第k(k∈[0,Nw])次预防性维修后装备的故障率。笔者将可用度模型分为r0≤rw和r0>rw两种情况进行分析。在保修期内,随着装备使用率r取值范围的变化,预防性维修间隔期和保修期限也随之发生改变,一般分为6种情况,如表1所示。 当r0≤rw时,r0和rw的相对关系如图2所示。 图2 r0和rw的相对关系 笔者详细地分析r≤r0时,装备的停机时间和可用度计算过程。 由表1可以看出: 当r≤r0时,为表1中第1种情况,预防性维修总次数Nw=⎣Tw/T0」。在每次预防性维修后,装备故障率λk(t|r)的变化如下: 1) 当k=0时, λk(t|r)=λ(t|r); (6) 2) 当1≤k≤N-1时, λk(t|r)=λ(t-kT0+(δ(m1)T0+ δ2(m1)T0+…+δk(m1)T0)|r)= (7) 3) 当k=N时, λk(t|r)=λ(t-kT0+(δ(m2)T0+ δ(m2)δ(m1)T0+…+ δ(m2)δk-1(m1)T0)|r)= (8) 4) 当N+1≤k≤Nw时, λk(t|r)=λ(t-kT0+((δ(m1)T0+ δ2(m1)T0+…+δk-N(m1)T0)+ (δ(m2)δk-N(m1)T0+ δ(m2)δk-N+1(m1)T0+…+ δ(m2)δk-1(m1)T0))|r)= (9) 当厂家和部队分别实施预防性维修保修策略,装备故障后进行最小预防性维修时,则在2个相邻预防性维修间隔期内,装备故障服从非齐次泊松过程[17]。因此,在相邻的预防性维修间隔期[Tl,Tu]内,最小预防性维修次数 (10) 式中:Tl和Tu分别为2个相邻预防性维修的时间。 由此可知:保修期中修复性维修造成的总停机时间 (11) 预防性维修造成的总停机时间 DP=Tp1(Nw-1)+Tp2。 (12) 因此,保修期内总停机时间 D=DP+DF=Tp1(Nw-1)+Tp2+ (13) 装备的期望可用度 (Tp1(Nw-1)+Tp2+ (14) 同理,可得其他5种情况下的装备停机时间和可用度,具体计算公式分别如下: (15) (16) (17) (18) (19) 对于使用率服从分布函数为G(r)的二维保修装备,当r0≤rw时,由式(14)-(16)可得保修期内装备可用度 (20) 当r0>rw时,由式(17)-(19)可得保修期内装备可用度 (21) 1) 在二维保修期(Tw,Uw)内,T0以ΔT0为步长在[0,Tw]内取值,U0以ΔU0为步长在[0,Uw]内取值,生成有限组(T0,U0)。 2) 在每组(T0,U0)中,确定预防性维修总次数Nw,并使N在[1,Nw]内遍历取值,得到不同的组合(T0,U0,N)。 2.2.1 算例 已知某新型装甲运输车为二维保修装备,保修期Tw=5 a,Uw=16×104km。为减少该型装备的故障次数、降低停运时间、提高可用度,采用厂家和部队分别实施预防性维修的保修策略。经专家评估,部队和厂家对该型装备实施预防性维修的程度分别为1级和3级,其对应的修复因子δ(m1)=0.74,δ(m2)=0.2。其他参数TF=1.5 d,Tp1=7.5 d,Tp2=10 d,α=3,β=0.72,θ0=0.7,θ1=0.5,θ2=0.6,θ3=1.0。 T0以步长ΔT0=0.03Tw在[0,Tw]内取值,U0以步长ΔU0=0.03Uw在[0,Uw]内取值,共生成1 089组(T0,U0)。计算每组(T0,U0)中N取不同值时,装备最大可用度A(T0,U0)。不同T0、U0的最大可用度A(T0,U0)如图3所示。 图3 不同T0,U0的最大可用度A(T0,U0) 在新保修策略下,二维保修装备可用度具有如下规律: 1) 当U0较小时,装备可用度受T0变化的影响较大;当U0较大时,装备可用度受T0变化的影响较小;当U0=0.13Uw、0.4Uw时,可用度受T0变化的影响如表2所示。由表2可知:当U0=0.13Uw时,装备可用度随T0的变化较大。因此,在预防性维修使用度间隔期确定的情况下,可根据U0的大小,并结合装备可用度的需求情况来调整预防性维修间隔期的长短。 表2 U0固定、T0变化时装备最大可用度 % 2) 当T0较小时,装备可用度受U0变化的影响较小;当T0较大时,装备可用度受U0变化的影响较大。因此,在预防性维修间隔期确定的情况下,可根据U0的大小,并结合部队对装备可用度的需求情况调整预防性维修使用度间隔期。 由此可知:当厂家和部队分别实施预防性维修的保修策略时,T0、U0和N中任一参数的变化均影响保修期内装备的可用度。 2.2.2 敏感性分析 由于新保修策略提出了保修期内由厂家和部队分别实施不同维修程度的预防性维修,则2种程度预防性维修的修复因子之比δ(m1)/δ(m2)直接影响装备可用度。为了分析δ(m1)/δ(m2)对装备可用度的影响,将δ(m2)作为变量进行敏感性分析,其他参数保持不变。当0.2≤δ(m2)≤0.6时,对比分析新保修策略和传统保修策略对装备可用度的影响,结果如表3所示。 表3 不同δ(m2)下2种保修策略对装备可用度的影响对比 笔者以二维保修装备保修期内可用度为研究对象,提出了包含2种维修程度的不完全预防性维修保修策略,建立了相应的装备可用度模型。通过算例表明:该保修策略可提高二维保修装备的可用度,满足部队对装备具有更高可用度的需求,也为厂家和部队制定保修决策方案提供了依据。通过敏感性分析可知:厂家实施预防性维修的程度越高,该策略的优势越明显。但是,笔者只考虑了保修期内厂家实施1次预防性维修的情况,下一步研究中一方面考虑厂家实施多次预防性维修;另一方面,由于在新保修策略中,装备可用度越高,保修费用也会随之升高,因此进行保修决策时,需要将装备可用度和保修费用进行综合权衡。1.2 模型建立
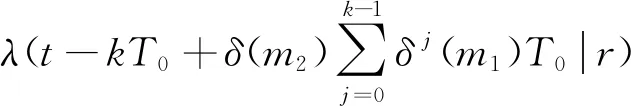
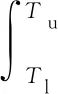
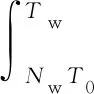


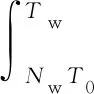
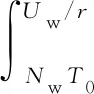
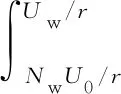
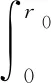
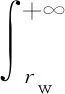

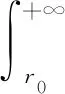
2 模型求解与算例
2.1 模型求解
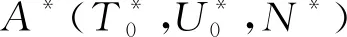

2.2 算例分析
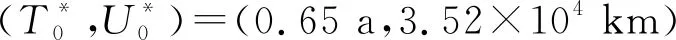

3 结论
