常见的三种三角函数值域的求法

周怡明 陈国林

(1.江西省上饶市上饶中学 334000;2.江西省南昌市东华理工大学理学院 330013)

一、y=asinx+bcosx+c型的三角函数值域的求法

(1)求∠B的大小；

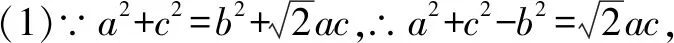
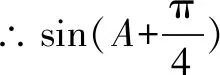
二、y=asin2x+bsinx+c型的三角函数值域的求法

例2 求函数y=cos2x-2asinx-a(a为常数)的最大值M.

解析y=cos2x-2asinx-a=-(sinx+a)2+a2+1-a，令t=sinx，则y=-(t+a)2+a2+1-a,(-1≤t≤1).

(1)若-a<-1时，即a>1时，在t=-1时，最大值M=a.

(2)若-1≤-a≤1时，即-1≤a≤1时，在t=-a时，取最大值M=a2+1-a.

(3)若-a>1，即a<-1时，在t=1时，取最大值M=-3a.

评注形如y=asin2x+bsinx+c的三角函数，可先设sinx=t，化为关于t的二次函数求值域.

三、y=asinxcosx+b(sinx±cosx)+c型的三角函数值域的求法

例3 求函数y=sinx-cosx+sinxcosx的值域．

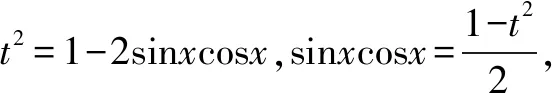
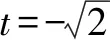
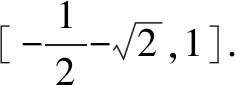
评注形如y=asinxcosx+b(sinx±cosx)+c的三角函数，可先设t=sinx±cosx，化为关于t的二次函数求值域．