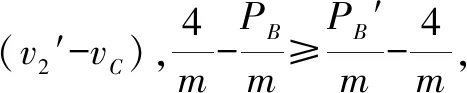质心法速算一维碰撞

谢汝成

(吉林省辽源市第五中学 136200)

一维碰撞问题是高考的重点和难点，但运算过程涉及到二元二次方程的求解，计算复杂，不易得出答案.此时可以引入质心系的相关知识，进行分析求解，能有效地减少计算时间，提高解题效率.

一、理论推导

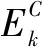
以质心为参考系，系统不受外力，总动量恒为零，质心系为零动量系.

结论两个物体发生一维碰撞前后，相对质心速度大小不增加.完全非弹性碰撞时，碰后相对质心速度等于零.

二、应用举例

1.如图2所示,在光滑的水平面上,一个质量为3m的小球A,以速度v0跟质量为m的静止的小球B发生弹性碰撞.求碰撞后AB两小球的速度各是多少?

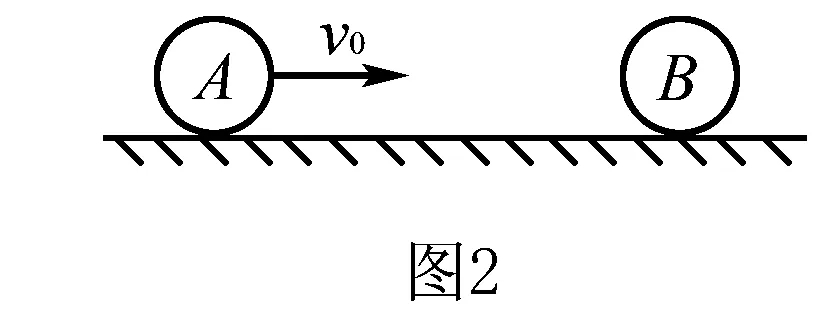
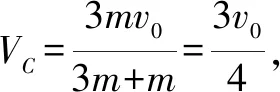
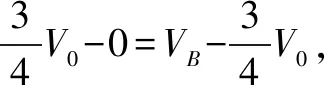
点评质心解法在此类问题中不涉及到平方的计算，有效的减少了计算时间，降低了错误的风险.如果题目中的B球有初速度，上述解法的优势将更加明显.

2.如图3所示,质量为m、速度为v的A球跟质量为3m、处于静止的B球在光滑的水平面上发生对心正碰,碰撞后B球的速度可能 ( ).

A．0.2v B．0.4v C．0.6v D．0.8v

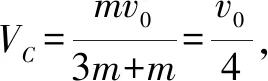
3．A、B两小球在光滑水平面上沿同一直线向同一方向运动，质量分别为m和2m，A球的动量为5kgm/s，B球的动量为 7kgm/s，当A球追上B球时发生对心碰撞，则碰撞后A、B两球动量的可能值为( )

A．pA′=4 kg·m/s，pB′=8 kg·m/s

B．pA′=3.5 kg·m/s，pB′=8.5 kg·m/s

C．pA′=3 kg·m/s，pB′=9 kg·m/s

D．pA′=2.5 kg·m/s，pB′=9.5 kg·m/s