跨越直观抽象过程直达素养
2019-11-23曹秋桦
曹秋桦

[摘 要]培养学生的抽象能力,需要教师通过直观的方式将抽象的数学知识更加形象地呈现出来,让学生经历观察、比较、综合、抽象、概括的思维过程,从而达到理解和内化。教师还需跨越直观,打通直观与抽象之间的通道,让学生沿着这条路径直达思维内核,建立起清晰的模型、知识体系,培养初步逻辑思维能力和数学核心素养。
[关键词]小学数学;核心素养;跨越直观;抽象思维
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2019)29-0074-02
数学抽象是指舍去事物的一切物理属性,提炼出数学研究对象的思维过程,主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并用数学符号或数学术语予以表征。数学抽象使得数学成为高度概括、准确表达、有序多级的系统。
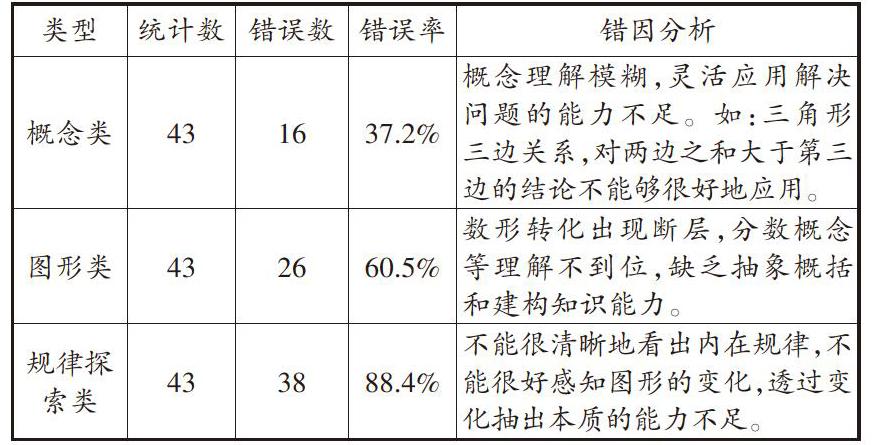
在做题时,学生对一些易错习题的理解不够透彻,对概念、图形等的抽象能力比较弱,于是我针对这些易错题做了分类。
这些问题反映出学生对知识的体验不深刻,对概念的形成过程不够熟悉,抽象概括能力比较弱;学生头脑中没有形成清晰的知识体系,不能进行有效的知识迁移。因此,培养学生的抽象能力是数学教学中不可忽视的一个问题,也是值得广大教师在实践中深入研究和探索的内容。
一、图释表达,让抽象的思维直观可视化
数学教学的主要目的在于培养学生的数学思维品质,而抽象的数学思维学生通常难以把握,需要教师通过直观的方式,将抽象的数学知识更加形象地呈现,便于学生理解和内化。
【例1】商中间、末尾有0的除法
师:306÷3的商大约是多少?你是怎样估算的?
师:结果到底是多少呢?请你们先尝试算一算。
师:你是怎么算的?为什么可以这样算?
(1)交流竖式
师:你们怎么计算306÷3?说一说计算过程。
生1:先用3个百除以3得1个百,接着用十位上的0除以3得到1个零,再用个位上的6个一除以3得2个一,最后将1个百加上2个一就等于102。
师:你们在解题的过程中遇到了什么新问题?
生2:被除数中间有0。
师:你们是怎么解决的?商的十位上为什么商0?
生3:因为被除数十位上是0,0÷3=0。
师:是呀,被除数的百位上正好被除尽,其十位上的0除以3得0,0商在十位上,个位落下来继续除。
(2)简化算式
師:有的同学这样写(如右图),这种写法合理吗?你们还有更简便的写法吗?
(3)借图释理
师:我们借助方格图来看一看306÷3的计算过程。
师:请用笔圈一圈、分一分,表示计算过程。
生4:只需要两步,先分百位上的3,3个百除以3等于1个百;再分个位上的6,6个一除以3等于2个一。因为十位上是0,0除以3等于0,所以十位上的分的过程可以省略。
师:十位上的这个0能不写吗?为什么?
生5:不能。不写的话就变成两位数了,跟我们一开始估算的结果——100多(三位数)不符。
师:如果被除数的中间、末尾出现0除以一个数,那么在商的相应位置上要用0占位。(板书:商0占位)
在“数的运算”的教学中,借助小方块等直观操作可以帮助学生形成表象,再通过交流进行适度抽象,同时及时地追问和引导,就能帮助学生沟通具体感知和抽象概括之间的联系,逐步将思维引向深入,实现对算理的意义建构。
二、适度跨越,让抽象的思维路径有迹寻
抽象是数学活动中的基本思维方法,也是数学的本质特征之一。数学抽象的对象可以是某种现实原型,但更多的是人们熟知的一些数学概念和结构,它是逐层递进的。教学需要直观,但也需跨越直观,打通直观与抽象之间的通道,让学生沿着这样的路径直达思维内核。
【例2】三角形的认识:认识三角形特征,建构三角形概念
(1)画一画,经历概念的形成过程
师:看了这么多,说了这么多,留在你心目中的三角形是怎样的呢?请画下来。
(学生典型作品展示,图略)
(2)说一说,语言呈现操作体验
师:你们是怎样画出这个三角形的?
生1:先画一条线段,然后在其中一个端点处接着画第二条线段,最后连起来。
师:谁也是按这个方法画的?我们俩能不能合作在黑板上再画一个?你来说,我来画。
生2:点出3个点,根据已有经验,先在两点之间画出一条线段,接着换一个点,画出第二条线段,连接剩下两点,画出第三条线段。
师:三角形由3条线段围成,3条线段应该需要6个点,为什么你只点了3个点就画成了?
生2:因为围成三角形的3条线段一条接着一条,每两条线段共用一个端点。也可以说这3条线段“首尾相接”。
(3)想一想,操作中体会3点不共线
师:那么是不是任意画3个点都能围成三角形呢?同桌讨论,再拿出方格纸试一试。
师:想象一下,3个点怎样放不能围成三角形?
师(总结):围成三角形的3个点不能在同一条直线上。
师(发散):有了这个发现,现在可以放心大胆地找第三个点了。你想把它摆在哪里?想象这个三角形的样子。大胆一些,第三个点还能摆在哪里?
(4)议一议,归纳概括三角形特征
师:回顾刚才的学习,我们交流了不同的画三角形的过程,也欣赏和想象了大小不一、形状各异的三角形,那么这些三角形都有什么相同之处呢?
生3:都是由3条线段围成的。
生4:都有3个点(顶点)、3个角和3条边。
师:以上两位同学总结的就是三角形的特征。
三角形是最常见的一种图形,也是最基本的多边形之一。学生已经积累了一些“空间与图形”方面的知识和经验,同时也具备一定的空间感与抽象思维能力,他们对周围事物的感知和理解能力,以及探索图形之间关系的愿望还在不断提高。
有关三角形定义的教学,教师是通过让学生在“画三角形”的操作活动中进一步感知三角形的属性,抽象出概念。首先,学生通过从点到线、从线到面的操作与观察中找出三角形的共同点,然后从画一画中发现和明确三角形的特征,最后通过一个疑问“3条线段应该需要6个点,为什么你只点了3个点就画成了?”,让学生尝试概括三角形的含义,着重理解“首尾相接”和“围成”两个关键词,建立正确的三角形概念。教师借助直观经验,把抽象的概念和具体的图形联系起来,引导学生发现三角形的特征,概括出三角形的定义。学生通过概念的内化与外显过程,逐步抽象出三角形的模型与其高的本质意义,发展了空间观念。
三、建立模型,让抽象的思维体系有架构
课程标准指出:“数学教学要让学生经历运用数学符号和图形描述现实世界的过程,建立初步的数感和符号感,发展抽象思维。”抽象有两个层次,一个是直观描述,另一个是符号表达。数学是抽象出来的符号体系,建立符号意识可以清晰、准确、简洁地表达数学思想、概念、方法和逻辑。数学抽象的主要表征形态是数学符号,数学符号是数学抽象思维的外壳。符号意识是数学抽象的衍生素养,数学抽象最终指向的是数学模型的建立和数学思想方法的形成,以及建立数学结构与体系的过程。
【例3】乘法分配律
(1)结合情境引发问题
师:同学们表演节目,男、女生分别按队形站,男生队形每行13人,有8行;女生队形每行11人,有8行。你能提出哪些数学问题?
生1:男、女生一共有多少人?
师:你会列式吗?
生1:13×8+11×8。①
师:还有别的算法吗?
生2:(11+13)×8。②
师:为什么这样算?为什么可以把它们合起来?
生3:因为男、女生都是8行。
(2)数形结合理解算理
师:你能用直观的图例表示①和②两个算式相等吗?
(3)多样验证解釋
(学生计算验证,得出乘法意义理解:13个8和11个8相加就是24个8相加)
师:如果女生队形每行增加2人,男生队形每行增加3人,两种算法的结果还相等吗?为什么?
生4:相等。13×8+16×8=(13+16)×8。③
师:再变一下,如果一个长方形长是a米,宽是8米,另一个长方形长是b米,宽是8米,两个长方形的面积之和是多少?
生5:a×8+b×8=(a+b)×8。④
师:观察这4个算式,你有什么发现?
(学生通过举例,归纳得出结论:a×c+b×c=(a+b)×c)
数学课程的一个重要任务就是让学生建立符号意识,懂得符号的意义,感受和掌握使用符号的能力,会运用符号解决实际问题,发展抽象思维能力。让学生经历“具体事物→个性化的符号表示→数学地表示”的符号化过程,才能有效提升数学素养。
培养学生的抽象能力,对他们学好数学、应用数学,培养初步逻辑思维能力和数学核心素养具有重要意义。史宁中教授说:“数学的表达是符号的,但教学应当是物理的;数学的证明是形式的,但教学应当是直观的;数学的体系是公理的,但教学应当是归纳的。”对于教师来说,不能为抽象而抽象,应结合具体的教学内容为学生选择恰当的、物理的、实际的情景,通过设计直观的操作活动帮助学生进行抽象归纳。数学抽象在教学中得以落实不是朝夕之功,需长期的研究和探索。
(责编 李琪琦)
