亲历学习过程渗透基本思想

高成香

[摘 要]课程标准在总目标中明确提出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”足可见数学的基本思想在数学教学中的重要性，这对于教师来说也是一个新的挑战。学习不仅仅是灌输，更应该是让学生亲身经历学习过程，在概念形成、操作以及巩固练习中感悟数学基本思想。

[关键词]小学数学;亲历过程;渗透;数学基本思想

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2019）29-0053-02

学生的数学学习应该是生动活泼的，而不是死记硬背、机械式的學习过程。相对于呆板、灌输式的教学，有感染力、活泼的课堂更容易被学生接受。有生命力的课堂才是当今教学真正需要的，这样的课堂对学生学习数学的影响是潜移默化的，使学生更加倾向于“知其然”且“知其所以然”的模式。它告别了单调的传统教学方式，给学生带来与众不同的学习体验与收获。学生只有亲身体验和经历知识的形成过程，才能对所学知识有更深入的了解，这样的学习过程，才是学生积累活动经验、感悟数学思想的过程。

一、亲历推导过程，渗透转化思想

学习苏教版教材五年级上册“图形面积计算”时，学生经常会出现“三角形面积=底×高”“梯形面积=（上底+下底）×高”等低级错误。教师此时如稍加提示，学生也能够快速回忆起正确的面积计算公式，这说明学生对知识掌握不牢，过于注重记忆结果而忽视了过程，用死记硬背代替了意义识记，导致学习过于片面，知识结构零散、不成系统。在实践过程中，为了增加学生的印象，丰富学生的体验与感受，教师应侧重于让学生主动经历操作、观察比较、概括的活动过程。

例如，教学“三角形的面积”时，我在课前准备了六个三角形。

师：选择两个三角形拼一拼，看看哪两个三角形可以拼成平行四边形？

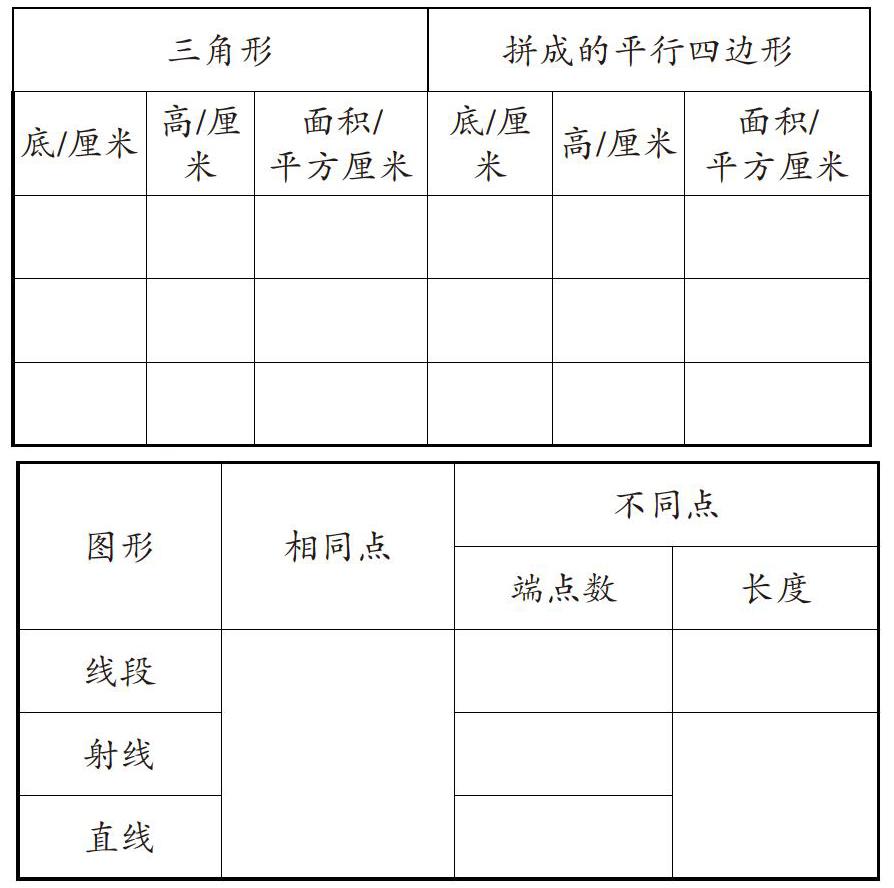
（学生动手拼一拼，并填写下表）

（小组交流，汇报）

师：能够拼成平行四边形的两个三角形有什么特点？

生1：两个完全一样的三角形能够拼成一个平行四边形。每个三角形的面积是平行四边形面积的一半。

师：拼成的平行四边形的底和高与三角形的底和高有什么关系？

生2：平行四边形的底和三角形的底相同，平行四边形的高和三角形的高相同。

师：每个三角形的面积与拼成的平行四边形的面积有什么关系？说说你的理由。

生3：两个完全一样的三角形能够拼成一个平行四边形，这样的一个三角形的面积是平行四边形面积的一半。

师：也就是说，我们可以把三角形的面积转化成平行四边形的面积，把未学过的转化成已经学过的。

师：你能说一说怎么求三角形的面积吗？

（同桌讨论，指名学生说一说推导过程）

在设计本课时，教师充分考虑到学生的基础，课堂中注重培养学生的动手操作能力，使学生通过直观的操作感受图形间的联系，加深了学生对三角形面积公式推导过程的印象，从而将未知的知识转化为已知的知识，便于学生理解和记忆。

二、经历画图过程，渗透数形结合思想

解决数学问题时，一般情况下先把题目中无形的信息转化成有形的信息。画图策略对学生理解题意、分析数量关系有着重要的意义，借助画图策略，学生可以将许多抽象的数学概念和数量关系形象化、简单化，恰当地借助直观图形让数量“可见”。数形结合是数学解题中常用的思想方法，它是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的思想方法。著名数学家华罗庚这样形容数形结合思想：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。”

在教学四年级“解决问题的策略——画示意图”时，学生直观地感受了数形结合的魅力和好处，意识到在遇到难题时，可以结合图形来拓宽思路。下面是我对教授画示意图的教学设计。

师（出示图片）：猜一猜这是哪里？

生（齐）：学校的花圃。

师：你们观察得真仔细！学校近期要扩建花圃，我们也来看看吧。

（教师出示题目：学校的长方形花圃原来长8米，扩建后，花圃的长增加了3米，面积增加了18平方米，求原来花圃的面积。）

师：看了题目，你们有什么疑问？

生1：“花圃的长增加了3米”是什么意思？

生2：要求出原来花圃的面积，就要知道原来花圃的长和宽各是多少。现在只知道原来花圃的长，那么宽该怎么求呢？

师：你们的疑问都很有意义。题目给出的条件和问题较多且乱，你能用其他方法将它们表示清楚吗？

生3：画示意图。

师：你觉得该怎么画？画什么呢？画图的过程中需要注意些什么？

（学生先独立思考，再全班交流）

生4：先画一个长方形，在长的下方标注“8米”。

师：如何在这个图中表示“长增加了3米”以及“面积增加了18平方米”？自己在图中试一试。

（学生尝试作图）

师：我们已经在图上清晰地表示出了条件，接下来如何表示所求问题？

师：你能根据示意图说一说数量关系吗？

在本课教学中，画图所占比重及影响之大，直接关乎学生的解题思路及最后结果。可见，画图是解题的关键。画示意图不仅能够直观明了地反映题中的条件和问题，而且是学生分析数量关系的“纽带”，为解决实际问题提供了肥沃的“土壤”。同时，画示意图也能培养学生数形结合的思想，为学生的数学思考奠定基础。

三、经历概念形成过程，渗透分类思想

在数学教学中，教师不能只关注结果，知识的形成过程也尤为重要，而概念的形成更是学生学习复杂问题的基础。学习不仅仅是知识的灌输，更是基本知识、基本技能的培养，以及在无形中提高能力、渗透数学思想、积累数学活动经验的过程。学习的过程也是数学思想的积累与渗透的过程。

例如，教学四年级上册“线段、直线和射线”时，我这样组织教学：

（一）情境引入

师（出示图片）：你能猜猜这是什么地方吗？

生1：上海。

师：你是怎么猜测的呢？

生1：我去过东方明珠广播电视塔。

师：老师选取了东方明珠广播电视塔的一部分，并把它描到黑板上，谁能说说这是我们学过的什么？

生2：线段。

师：线段有什么特点？

生3：有两个端点、可以测量、直的。

师：是的，这样的图形就称为线段。

师：图片上的东方明珠广播电视塔真美，你能说说美在哪里吗？

生4：灯光是五彩斑斓的。

师：这些光线是线段吗？说说你的想法。

师：这些光线都可以看作射线。

（二）教学射线和直线

师：想象一下，把线段的一端无线延长，就成了射线。（板书“射线”，并画图展示）

师：自己画一画，并说说射线有什么特点。

生5：射线是直的，它只有一个端点，而且无限长。

师：如果将线段的两端都无限延长，就成了直线。（板书“直线”，并画图展示）

师：自己画一画，并和同桌说一说直线有什么特点。

生6：直的、没有端点、无限长。

（三）对比发现

师：比一比，线段、射线和直线有什么相同点和不同点？完成表格。

（四）反馈练习

（教师出示不同的图形，让学生分类）

师：题目中有曲线，而线段、射线、直线都是直的，分类时要注意区分。

数学因思想而深刻，在小学数学课堂教学中渗透数学的基本思想尤为重要。教师应该更新教育教学观念，多思考多实践，将数学的基本思想融入实际教学中，充分挖掘教材，充分利用校内、校外资源，将生活与数学结合，利用多媒体等资源进行整合教学。将来，学过的知识可能会被學生遗忘，但基本数学思想却能够长留于其心中，在他们的学习、生活、工作中发挥作用。因此教师应注重学生亲身经历知识的习得过程，从而达到“润物细无声”的效果。

[ 参 考 文 献 ]

[1] 中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[2] 王飞.小学数学教学中数学思想方法浅谈[J].才智，2017（30）.

[3] 陈小燕，陈岳婷，王李茹，吴冰.浅谈数学思想方法在小学数学教学中的渗透[J].才智，2017（30）.

（责编 李琪琦）