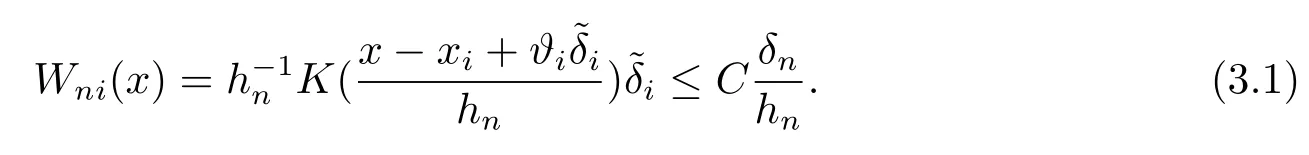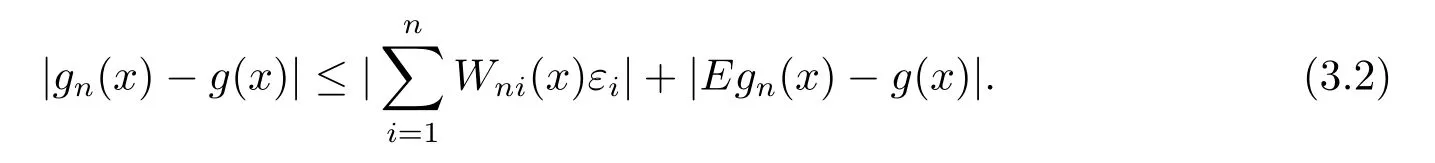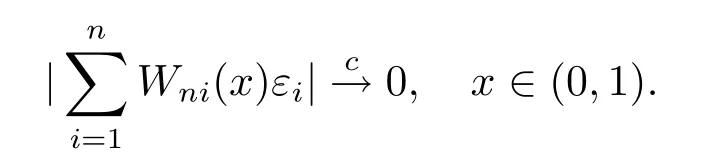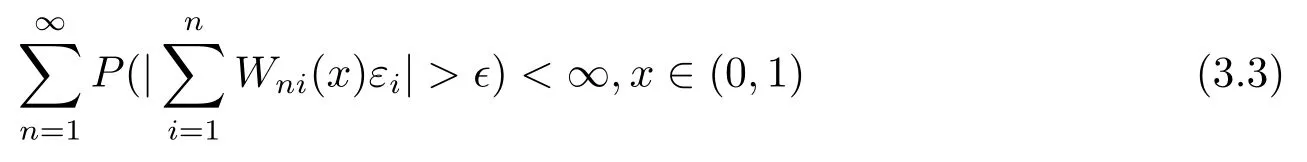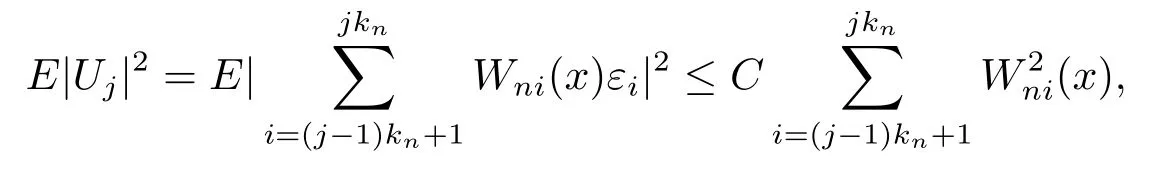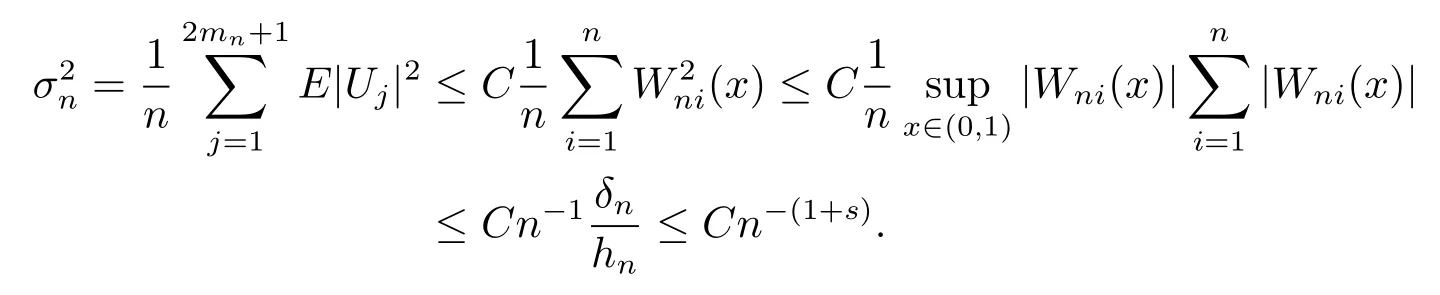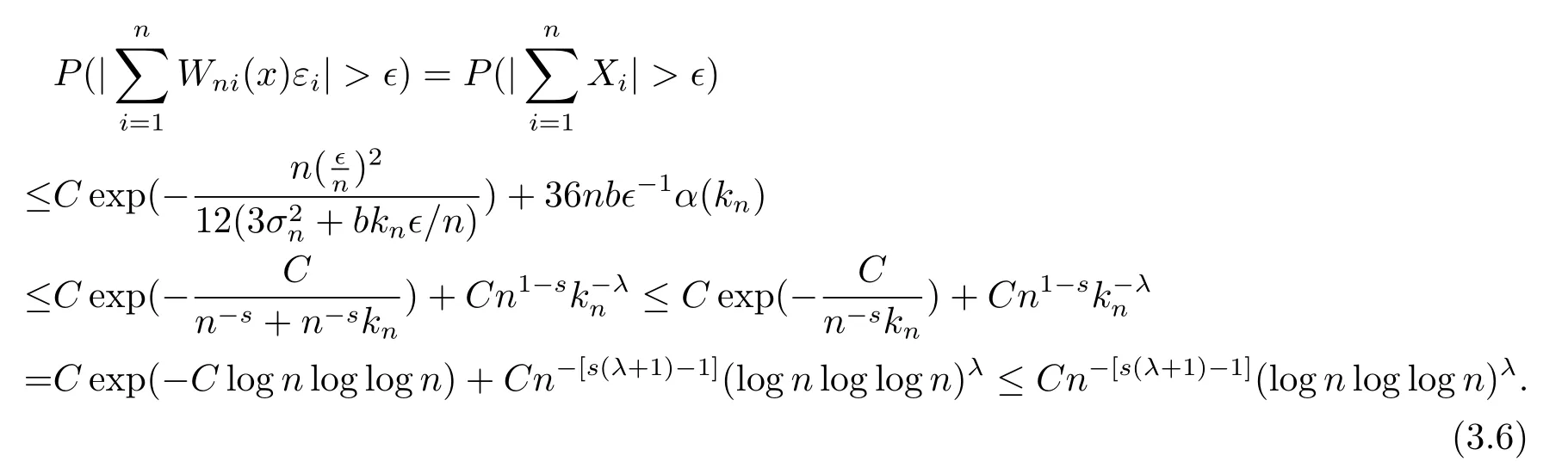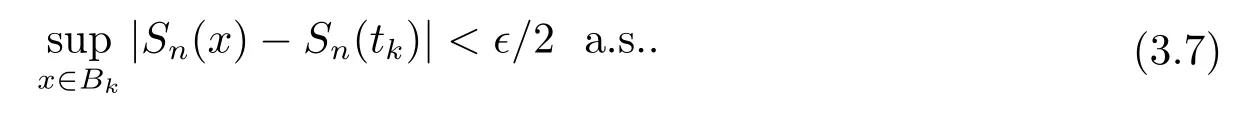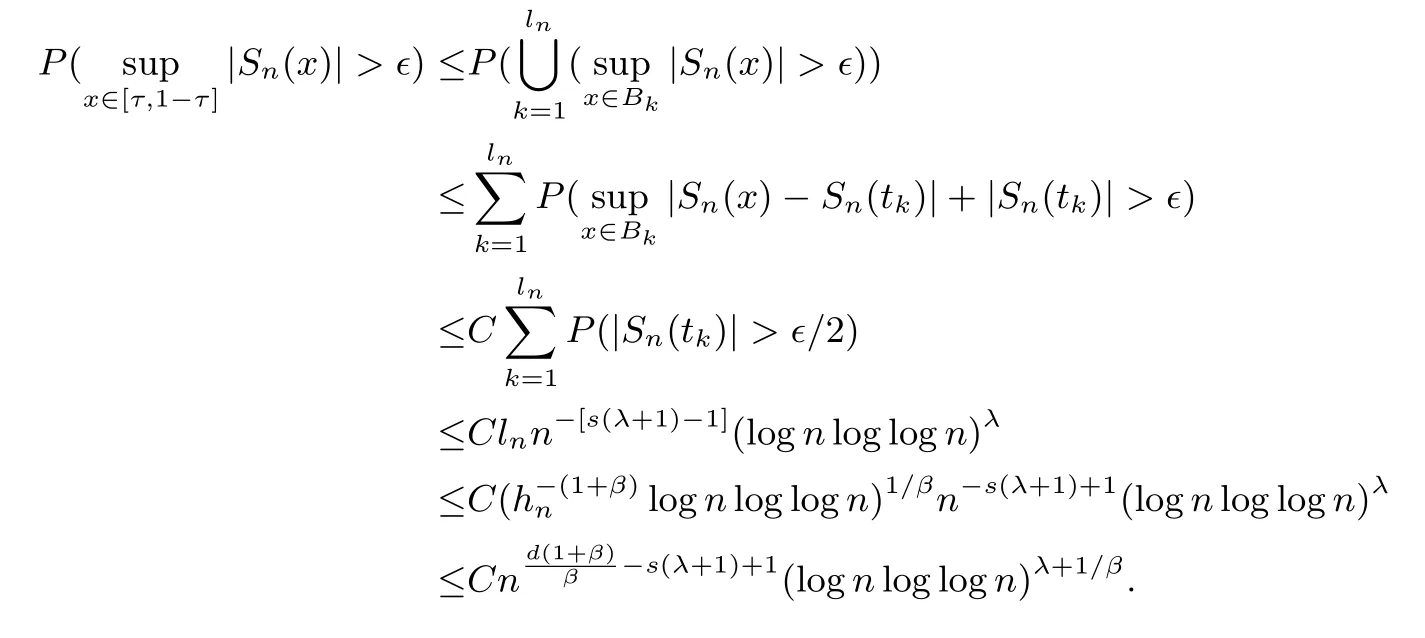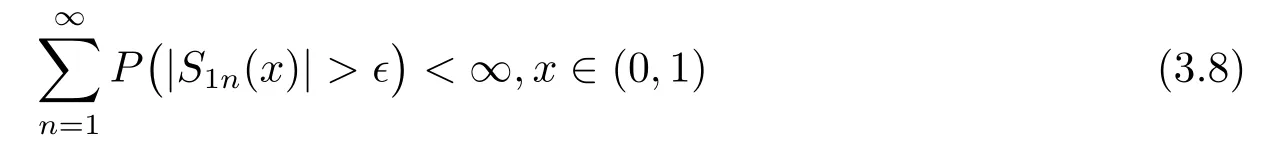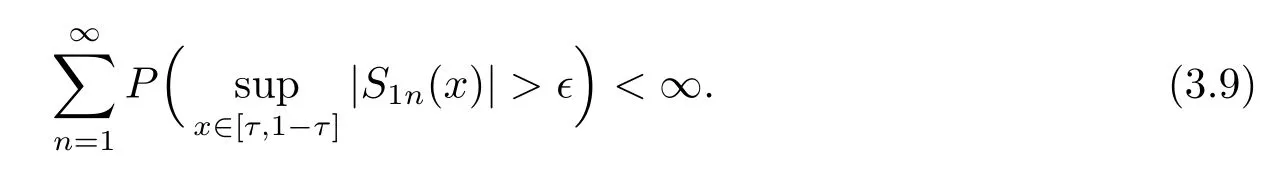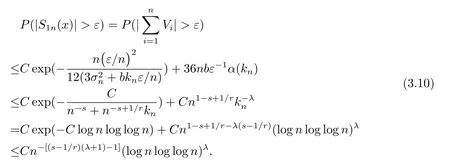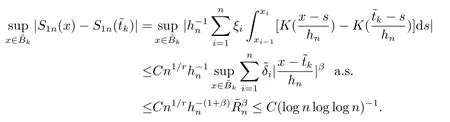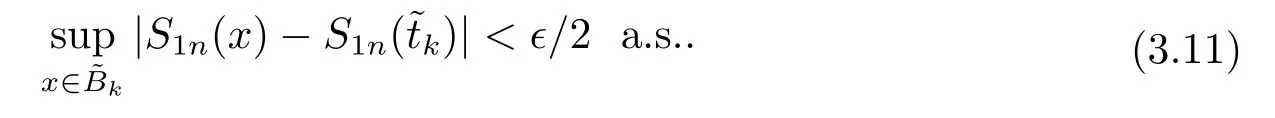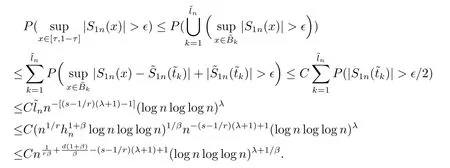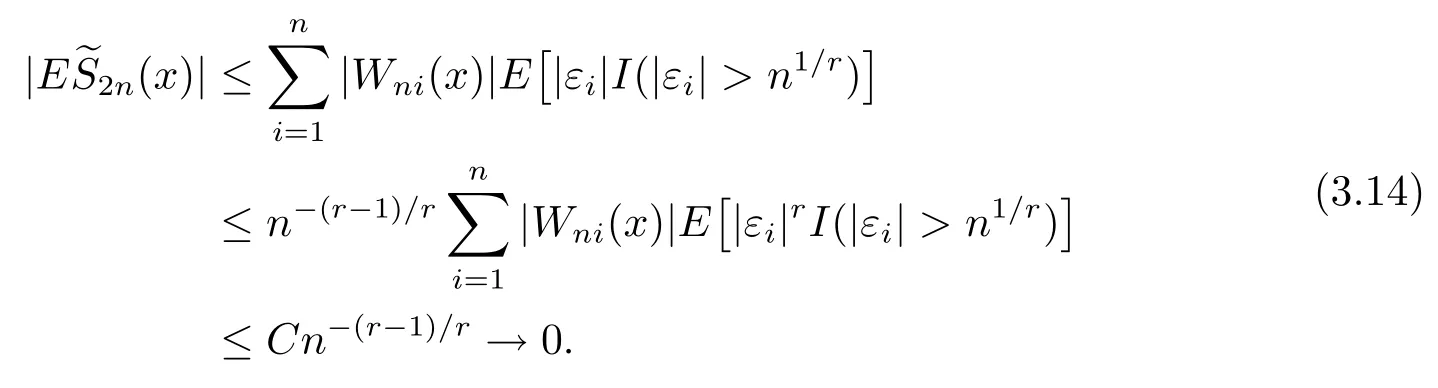α 混合样本下积分权回归估计的强相合性
2019-11-23杨秀桃杨善朝
杨秀桃, 杨善朝
(1.海口经济学院网络学院应用数学教研室, 海南海口 571127)
(2.广西师范大学数学与统计学院应用统计教研室, 广西桂林 541004)
1 引言
设N 为自然数集, {Xi;i∈N} 是概率空间(Ω,A,P) 上的随机变量序列.
定义1.1对随机变量序列{Xn;n≥1}, 如果当n→∞时,

其中σ域则称{Xn;n≥1} 是α混合的.
设Y1,Y2,··· ,Yn是固定点x1,x2,··· ,xn的n个观察值, 适合回归模型
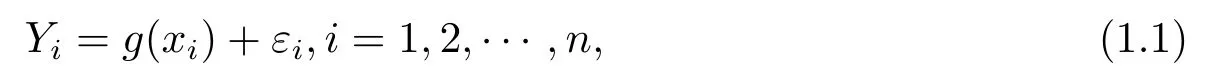
其中回归函数g(x) 是[0,1]上的未知函数, 且当x[0,1]时, 令g(x)=0, {εi} 是随机误差序列.
假定0=x0≤x1≤···≤xn−1≤xn=1.考虑Gasser 和Mller[1]对回归函数g(x) 提出的一种积分权核估计

其中核函数K(u) 是R1上可测函数, 且当n→∞时, 0 α混合序列是一类重要的非独立序列, 引起了诸多学者的关注.在α混合序列下, 文献[2]研究了回归加权核估计的强大数律; 文献[3]研究了一般回归加权函数估计的一致渐近正态性; 文献[4]研究了核型分位数估计的渐近正态性; 文献[5]讨论了风险度量ES 非参数估计部分和的渐近正态性; 文献[6]讨论了回归加权核估计的强相合性.讨论研究该混合序列背景下的非参数估计的大样本极限性质可更好地为进一步的实证研究提供理论基础.不少文献(如[7–15]) 讨论了在独立情形与混合相依情形下Priestley-Chao 加权核回归估计的完全收敛性和强相合性, 获得了很好的结果.早期, 对于文献[1]中Gasser 和Mller 提出的一种积分权核估计(1.2), 文献[16–18]研究了独立序列情形下估计(1.2) 的完全收敛性、渐近正态性等大样本性质.另外, 文献[19–21]给出了研究α混合随机变量序列大样本性质所需的部分和、加权和的不等式工具.较少文献在α混合序列背景下研究估计(1.2) 的大样本极限性质.本文则在α混合样本下给出回归函数核估计(1.2) 的强相合性与一致强相合性结论.利用文献[21]的指数不等式, 在较弱的条件下, 本文得到较理想的收敛结论.由于在α混合样本下研究具体的统计估计问题还是比较少, 因此本文的研究是有意义的. (b)g(·) 在[0,1]上一致连续; (c) 当n→∞时,hn→0,δn→0. 定理1.2设基本条件(a)–(c) 成立.又假设(i)Eεi=0,i=1,2,··· ,n, 且|εi|≤ba.s.;(ii) {εi} 为α混合相依, 且α(n)=O(n−λ), 其中λ>1; (iii) 当n→∞时, (1) 若 (2) 若存在d>0 使得ndhn→∞以及 则对任给的0<τ<1/2, 都有 注定理1.2 给出了α混合相依序列有界情形下, 估计(1.2) 的强相合与一致强相合性. 下面的定理1.3 是在该序列无界条件下得到该估计的强相合与一致强相合性. 定理1.3设基本条件(a)–(c) 成立.又假设(i)Eεi=0,i=1,2,··· ,n, 且∞, 其中r> 2; (ii) {εi} 为α混合相依, 且α(n)=O(n−λ), 其中λ>r/(r−2); (iii) 当n→∞时, (1) 若 (2) 若存在d>0 使得ndhn→∞以及 则对任给的0<τ<1/2, 有 为了证明定理的结论, 本节给出一些引理. 引理2.1[19]若{Xi;i≥1} 是零均值的α混合随机变量序列, 且{ai;i≥1} 是实数列. (i) 如果E|Xi|2+δ<∞, 这里δ>0, 则 (ii) 如果|Xi| 引理2.2[21]令{Xi;i≥1} 是零均值的α混合随机变量序列, 且|Xi|≤b< ∞a.s., 进一步假定正整数kn满足1≤kn≤n/2.则对任意的>0, 有 引理2.3设g(x) 在[0,1]上一致连续,如果hn→0 和δn→0, 则 对任给的0<τ<1/2, 有 证由(1.1) 和(1.2) 式, 有 从而 要证明(2.4) 式, 只需分别证明: 对x∈(0,1),In1(x) →0 和In2(x) →0.记B1=由g(·) 在[0,1]上一致连续知,∀ε>0, 当n充分大时, 有 所以In1(x)→0.另一方面, 由条件有 当n充分大时, 由条件知 注意到g(x) 在[0,1]上有界, 记取δ>0, 可有 由g(x) 在x处连续以及知,∀ε>0, 当n充分大时, 有 即 由(2.9), (2.10) 和(2.13) 式知,In2(x) →0.从而(2.4) 式成立.由于g(x) 有界, 所以上述证明过程对(2.5) 式也成立.证毕. 引理2.4设且hn→0, 则对任意的x∈(0,1), 有 而对任给的0<τ<1/2, 有 证对任意的x∈(0,1), 令显然 和 联合(2.16)–(2.18) 式得结论(2.14).另外, 对任给的0<τ<1/2, 有 和 由(2.16), (2.19) 和(2.20) 式得结论(2.15).证毕. 引理2.5[14]设{Zi;i≥1}是随机变量序列,若存在常数ρ>0,使得E|Zi|=O(i−(1+ρ)),则收敛. 由于 由(3.2) 式、引理2.3 以及Borel-Cantelli 引理可知, 定理1.2 与定理1.3 的证明归结为证明如下式子 与 又由引理2.4 及条件(a), 当n→∞时, 可有 定理1.2 的证明首先证明(3.3) 式.记Xi=Wni(x)εi, 由条件(i) 及(3.1) 式, 有EXi=0, 且有由于α(n)=O(n−λ) 且λ> 1, 所以在引理2.1 中的根据引理2.1 的(2.2) 式可得 又根据(3.1)、(3.5) 以及(1.3) 式, 可有 取kn=ns/(lognlog logn), 其中0 由(1.4) 式知, (3.3) 式成立. 其次证明(3.4)式.选取ln个中心在t1,t2,··· ,tln,半径为的邻域覆盖[0,1], 其中由条件(i) 知和基本条件(a) 知K(·) 满足β阶Lipschitz 条件, 对正整数k,1≤k≤ln, 可得 由(1.5) 式知, (3.4) 式成立. 定理1.3 的证明令 则有 与 记Vi=Wni(x)ξi, 显然有EVi=0, 且由条件(3.1) 式有Cn−s+1/r.现在对序列V1,V2,···, 利用引理2.2, 为此令由于α(n)=O(n−λ) 且λ>r/(r−2), 所以在引理2.1 中的 根据引理2.1 的(2.1) 式可得 又根据(3.1)、(3.5) 以及(1.6) 式, 可有 由(1.7) 式知, (3.8) 式成立. 结合条件(1.8) 知, (3.9) 式成立. 与 由(1.6) 与(3.1) 式, 可得 因此(3.3) 与(3.4) 式成立, 定理1.3 得证.




2 引理
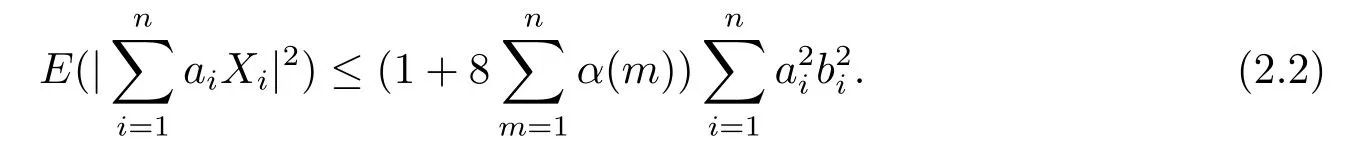

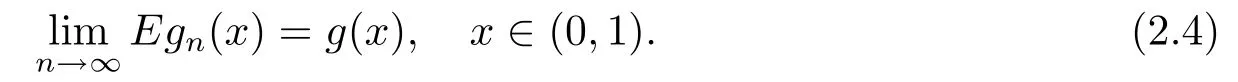
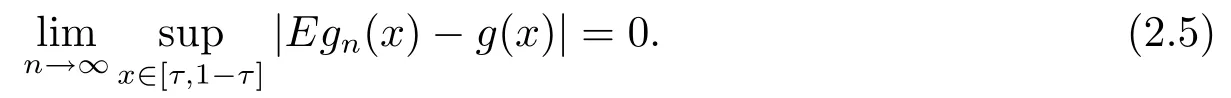
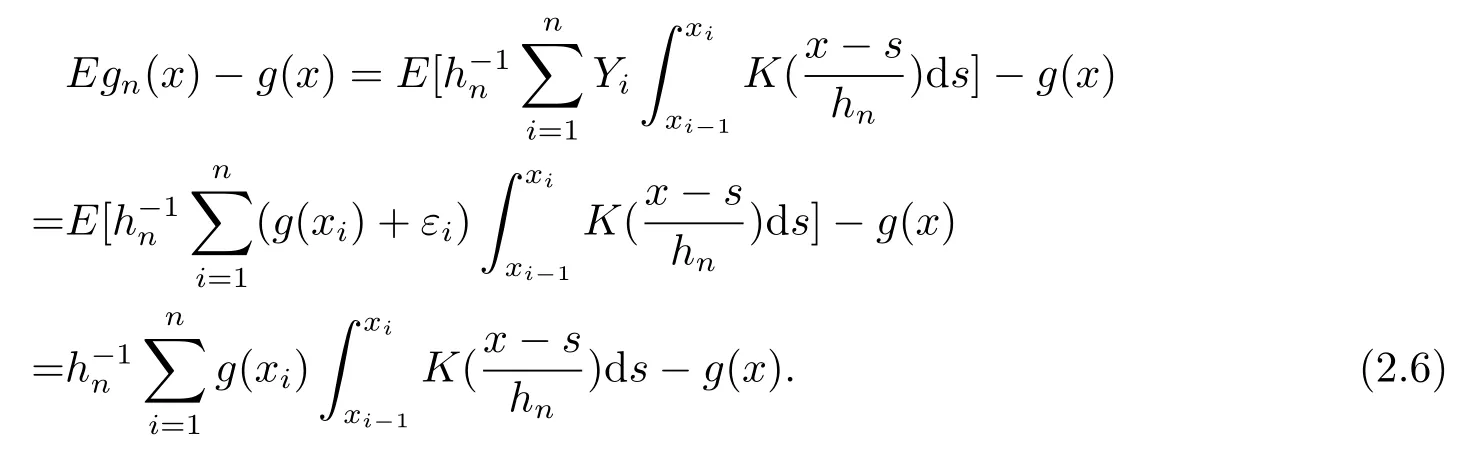

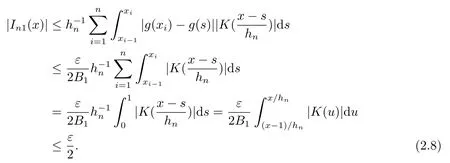
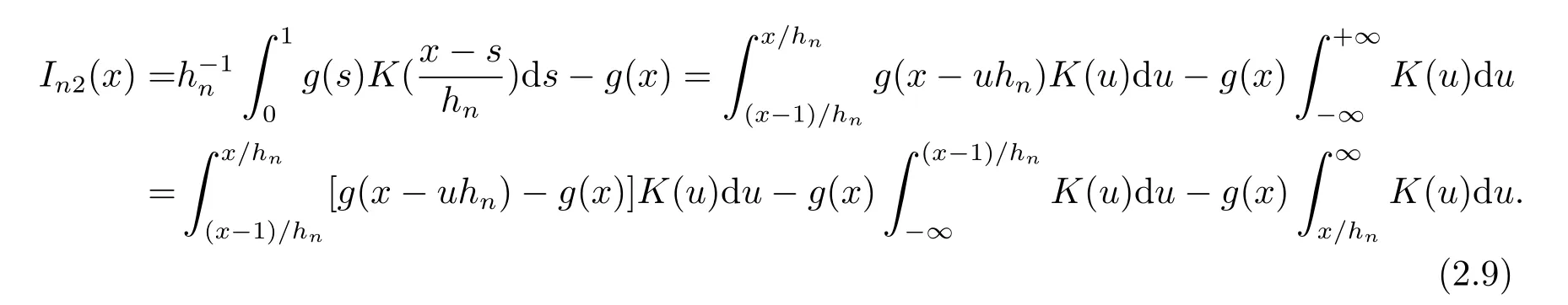

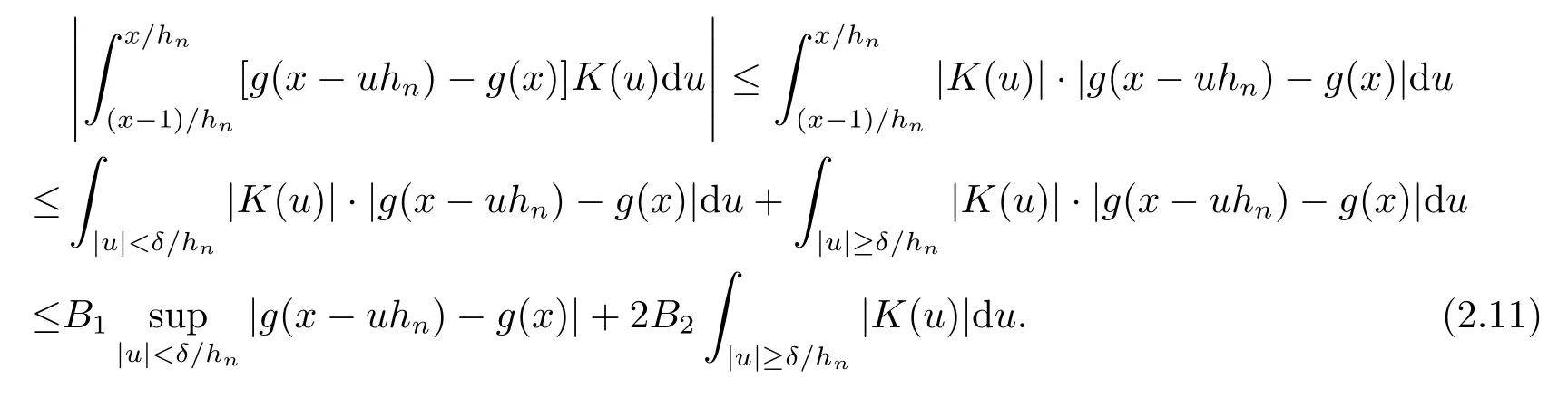





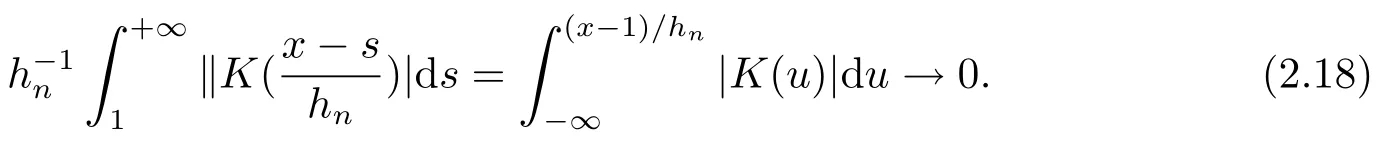
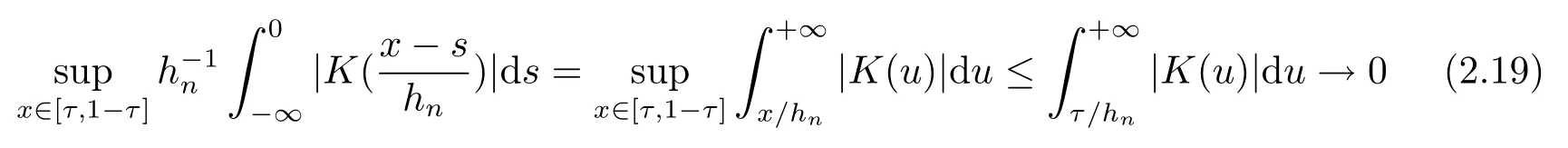
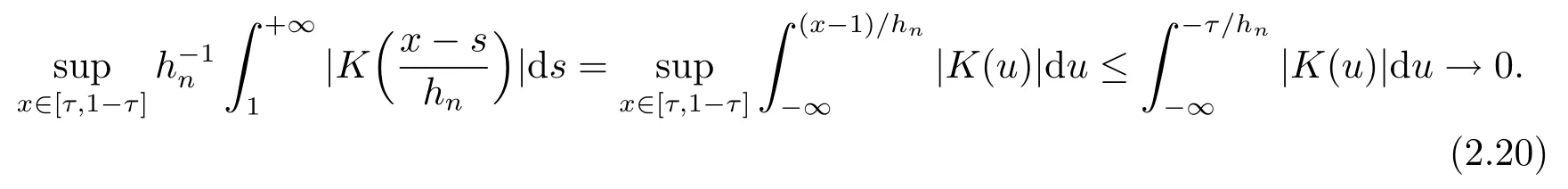
3 定理的证明