大型空间相机柔性支撑结构的设计
2019-11-23汪纯鹏刘波
汪纯鹏,刘波
(中国科学院长春光学精密机械与物理研究所,长春 130033)
随着空间相机的发展,不满足于低分辨率相机的需求促使其向高分辨率、大口径、长焦距的方向发展[1]。高分辨率大型空间相机意味着其搭载的光学系统需要更高的精度[2]以及更小的变形输入,故在光机系统与卫星平台间采用柔性支撑结构,以减少卫星平台由于温度及装配精度等产生的变形对光机系统的影响[3]。基于各类荷载对发射镜的三点柔性支撑的经典结构[4],以及LMSSC公司空间近红外相机的六点柔性结构[5]、韩国空间光学中心研制的bipod支撑结构[6]及长春光机所研制的Cartwheel柔性支撑结构[7]的研究,本文设计了一种大型柔性支撑结构,用于连接光学系统及卫星平台,并通过一定的柔性环节隔衰减变形。
本文研究的柔性支撑结构对于大型空间相机来说,力学性能基频不小于15 Hz,强度满足要求且具有10倍变形衰减能力,对柔性支撑结构的空间布局等相关参数进行了设计,并利用仿真进行了强度及柔性校核。其结果表明所设计的柔性支撑结构可以满足各项力学性能要求。
1 柔性支撑结构的设计
针对某大型空间相机研制任务,在光学系统光具座与卫星平台间需设计一套柔性支撑系统。要求保证光机系统稳定性,减小卫星平台变形影响及互相耦合;同时要求柔性支撑结构保证光学相机整体刚度,且满足动、静力学特性要求。且由于卫星平台在使用不同电器时造成不同温度场的不确定性,故在校核柔性支撑系统时将热变形转换为干扰位移。针对上述要求对柔性支撑系统提出以下指标需求:(1)固有频率不小于15 Hz;(2)在支撑光学系统1.2g重力荷载下留有一定安全系数;(3)当卫星平台端产生的变形传递至主光学系统光具座时通过柔性环节应衰减10倍。经由以上需求,本文设计了由六根两端具有柔性缩颈的细杆组成的柔性支撑系统(以下简称为六杆支撑系统或六杆),如图1所示。

图1 六杆支撑系统
六杆支撑系统形成准静定安装,每对连杆形成二脚架结构,三组二脚架呈120°分布。每根连杆两端采用圆柱形细颈形成柔性铰链,起到增大弯曲柔度的作用。六杆系统的作用主要是隔离卫星平台与外层结构由于热不均匀性等引起的变形干扰,保证光学系统结构稳定性[8]。
2 杆系参数的确定
六杆系统设计包括杆系空间布局和连杆柔铰参数的确定,根据连接刚度、连接柔度和柔铰强度等指标进行设计,主要流程如图2所示。首先通过连接频率(固有频率不小于15 Hz)分析得出杆系空间布局,然后利用以地面载荷(1.2 g重力荷载)为输入的强度分析确定柔铰直径,最后进行柔度分析(10倍变形衰减)从而确定柔铰长度。

图2 六杆参数确定流程
2.1 柔性支撑空间参数的确定
对于六杆支撑系统的指标要求为基频大于15 Hz且满足强度需求。六杆组件每两根连杆形成一个二脚架组,三组二脚架中心对火箭中心呈120°分布,连杆上、下端点分别在公共圆上,其它空间参数还包括每组二脚架的跨距和连杆的倾角。
杆系空间布局对整体连接刚度影响很大,所以以杆系连接一阶固有频率最大为优化目标,根据总体要求,连杆下端为固定状态。通过前期分析计算,在某一公共圆尺寸下,杆系空间分布包络应呈上圆小、下圆大的锥台形状。
与连杆上端连接的光具座如图3所示,其可行连接区域已较为受限,取其公共圆直径为3.2 m,且二脚架跨距无法相同,取X1为1.1 m、X2为1.6 m。根据空间限制,取杆系下公共圆直径3.4 m,对应的跨距设为Y1和Y2,即为优化变量。
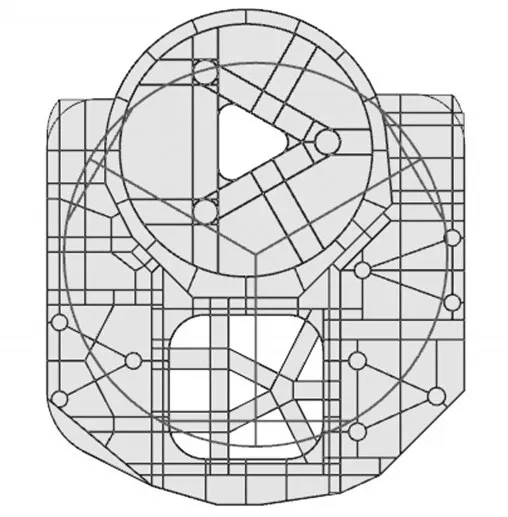
图3 光具座与六杆连接点分布图
建立简化有限元模型,进行二优化变量的可行空间搜索,得出一阶频率变化特性,如图4所示。在Y1与Y2的整个可行搜索空间出现两个独立的一阶频率最大峰值,其所形成的连杆组系分别呈“A”型和“V”型支撑布局,如图5所示。进一步根据卫星平台端的空间限制,杆系空间布局最终取为“V”形布局,如图5(b)所示。

图4 六杆空间布局与频率分布图
表1为两种构型的Y1和Y2最优解值,以及一阶与二阶固有频率,其振型分别为相互垂直的两个方向的摇晃,可以看出两阶固有频率值都非常接近,说明最优的杆系分布在各个方向都具有均衡的支撑。

表1 两种构型下的一阶与二阶频率

图5 六杆布局图
2.2 杆端柔性铰链参数的确定——直径
为使连杆近似具有二力杆特性,从而使杆系形成静定支撑,在连杆两端设计有圆柱形细径柔性铰链,以增加端部弯曲柔度,代替球铰配合副。
在杆系空间布局确定的条件下,建立有限元模型。以地面1.2倍重力加速度为质量载荷,分别计算杆系支撑侧向悬臂和竖立两种状态下的连杆柔铰应力,结果如表2和表3所示。对比两表,可以看出:(1)悬臂状态应力大于竖立状态应力;(2)弯应力较小,即连杆受力以轴力为主,与二力杆接近;(3)综合应力与柔铰长度关系很小。

表2 相机悬臂状态柔铰应力
若柔铰材料取为钛合金,其屈服强度为800 MPa,安全系数取为6倍,则使用强度为800 MPa/6,则柔铰直径大于15 mm便可满足强度要求,考虑其它未知因素所需要的强度余量,取为20 mm。

表3 相机竖立状态柔铰应力
2.3 杆端柔性铰链参数的确定——长度
在六杆系统的隔离作用下,针对热不均匀性变形的实际情况,将热变形转换为干扰位移0.1 mm并输入到六杆下端,此时要求光具座下表面变形小于10 μm。由于此干扰位移是由热变形所转换,故干扰位移的方向从空间上可分为面外(轴向)及面内(周向、径向)两种。通过前期模拟,六杆系统对面内的干扰位移具有非常优异的衰减能力(50倍以上),故本文中仅针对轴向干扰位移进行讨论。
在柔铰直径确定的情形下,其长度越大,则柔度越大。建立有限元模型,变化柔铰长度,考察在不同干扰位移作用下的光具座变形量。假设在六杆下端施加三种干扰位移:(1)±0.1 mm的轴向交错;(2)±0.1 mm的两点翘边(1组二脚架);(3)0.1 mm的单点翘边。长度为40 mm的光具座变形数据如表4所示,可见,此长度下的柔性铰链的柔度满足输入0.1 mm量级干扰下的隔离要求。表4中同时列出各干扰位移时所产生的柔铰应力(综合),也满足强度要求。三种工况下的光具座变形数据如图6所示,可见三种工况下光具座变形均在微米量级,变形量较小。

表4 光具座变形和柔铰应力
2.4 固有频率的校核
根据以上分析结果,柔铰直径为20 mm,长度为40 mm,同样建立简化有限元模型,进行模态分析,一阶和二阶固有频率分别为36.21 Hz和36.27 Hz。该频率是在对光学系统简化模型基础上得出的,其主要弹性环节仅为柔性铰链,所以真实结构的固有频率可能低于该值。

图6 三种工况下的光具座变形数据图
3 结论
本文根据某大型空间相机的设计要求,进行了光学系统与卫星平台间支撑结构的设计。通过基频的计算,确定了空间参数布局的最优解,并根据光学系统的稳定性对支撑结构提出了柔性支撑方案。利用地面荷载及变形干扰,对柔性支撑结构的杆系参数进行了确定。最后,进行了强度校核。通过合理的空间布局及杆系参数的确定,该柔性支撑结构满足了基频15 Hz,10倍变形衰减的力学性能要求且强度上预留了6倍以上的安全裕度,说明支撑系统能够满足空间应用要求。本文设计的六杆系统由于实际使用时光具座的连接点选择范围较为受限,故在本文中未涉及六杆系统光具座端的空间参数设计,但在前期分析中可以看出六杆光具座端的空间参数对六杆系统的使用效果也具有较大影响,设计时也应予以关注。本文的设计内容可为同类大型空间相机的设计提供一定的参考和借鉴。
