变负载流量调节阀电液伺服作动系统研究
2019-11-22朱美印裴希同但志宏
姜 震,王 曦,朱美印,裴希同,张 松,但志宏
(1.北京航空航天大学能源与动力工程学院,北京 100191;2.先进航空发动机协同创新中心,北京 100191;3.航空发动机高空模拟技术重点实验室,四川绵阳 621000)
1 引言
高空模拟试验台(简称高空台)能在地面上模拟发动机空中工作环境条件,是先进航空发动机研发过程中必不可少的关键设备[1-3],其进气调节装置一般由各种流量调节阀组成。在环境模拟试验中,宽广的飞行包线和起动到推力最大的状态变化,会导致流量调节阀上的气动负载变化极为巨大,其进口气体压力的变化范围和变化率分别可达到0~379 kPa 和12 kPa/s[4]。流量调节阀的伺服作动性能直接影响宽广飞行包线范围内发动机高空飞行环境的模拟效果,在工程中一般采用电液伺服控制系统对其精确调节来实现。
对于电液伺服控制系统的负载国内外均开展了相关研究。如Milić等[5]考虑了负载的弹力与阻尼力对电液伺服系统的影响,并在此基础上开展了位置鲁棒控制研究;王春行[6]在负载为弹力与阻尼力情况下研究了电液伺服系统的动态特性;郑晓华等[7]在电液伺服摇板式造波机控制系统中,将造波负载力考虑为惯性负载和粘性负载进行处理;付永领等[8]针对电液伺服位置控制系统压力脉动问题,建立了包括负载重力、摩擦力及弹簧力的负载力数学模型,仿真分析了负载力变化对系统的影响。但均缺少对流量调节阀气动变负载问题更一般的适用性的研究。
为此,本文通过分析流量调节阀动力特性,提出一种建立变负载电液作动机构模型的建模方法。建立开环变负载模型,并在同等条件下与试验数据进行对比分析以验证该方法的有效性,设计闭环回路并对闭环变负载电液伺服控制系统的跟踪性能和抗干扰性能进行仿真验证。
2 变负载动力学问题
某高空台特种流量调节阀(图1)[9-10]在整体上分为前壳体、中间壳体、后壳体三部分。前壳体上装有二级、四级、八级固定阀瓣,中间壳体为固定圆盘,后壳体上装有角度可调的无级盘。传动机构中液压作动筒活塞杆作直线运动,并推动由连杆连接的无级盘作圆弧运动,其几何运动关系如图2 所示。当进行发动机高空性能模拟试验时,飞行高度和飞行马赫数确定对无级盘角度的调节指令,流量调节阀前后的气流压力随之变化,从而使作用在无级盘上的气动负载改变。
调节过程中,无级盘与中间壳体的相对运动将产生变摩擦力矩Mf。设无级盘单位面积上的气动压力为fg,取如图2 所示的面积微元,则单位面积微元上的摩擦力为:

式中:μ为无级盘与壳体间的摩擦系数。
计算该摩擦力对盘心的力矩微元并积分可得:


图1 特种流量调节阀结构示意图Fig.1 Special flow regulating valve structure

图2 作动筒推动无级盘运动示意图Fig.2 Actuator pushes the motion of the valve plate
定义变气动负载力为Fg,则

由图3 中间壳体与无级盘的相对位置关系可确定Fg。记无级盘后气体压力为p2、作用面积为S,无级盘上受来流气动压力为p1、作用面积为S1,则


图3 无级盘与壳体的相对位置示意图Fig.3 The relative position of the plate and middle shell
活塞杆与无级盘间连杆长度很小,活塞杆作动力F可近似为沿圆周切向直接作用在无级盘上,则

式中:J=0.5mR2,为无级盘转动惯量;m为无级盘质量;,为无级盘角加速度;x为活塞杆位移。变换可得:

上式表明,将无级盘与活塞杆视为等效运动体,其等效质量为M=0.5m,变气动载荷的等效负载力FL为。则变气动负载与活塞杆作动力的动力学方程如式(8)所示,其动力学关系如图4 所示。


图4 变气动负载与活塞杆作动力的动力学关系Fig.4 Dynamical relationship between variable aerodynamic loads and piston rod force
3 变负载电液作动机构模型
电液作动机构包括电液伺服阀、液压作动筒及负载。下面首先考虑电液伺服阀的建模问题。电液伺服阀模型主要由流量特性和压力特性表示。AMESim 一般采用三位四通液压阀元件表示电液伺服阀,其接口参数主要由额定电流、额定压力、额定流量、自然频率和流通面积组成。前四项可根据电液伺服阀设计计算结果确定,而流通面积需要由空载流量特性来确定。其空载流量特性如图5 所示。

图5 电液伺服阀空载流量特性Fig.5 Electro-hydraulic servo valve no-load flow characteristics
建立空载流量模型以确定面积修正量,图6 为修正前后的空载流量特性曲线。修正前模型默认的流通面积导致其流量偏小,乘以修正系数1.403 得到修正后流量,符合空载流量特性。

图6 修正前后空载流量特性曲线Fig.6 No-load flow characteristic curve before and after modification
根据液压作动筒额定负载的设计要求,确定液压作动筒内径和活塞杆径,同时给出额定负载、额定供油压力下电液伺服阀的压力特性曲线(图7)。

图7 电液伺服阀压力特性Fig.7 Pressure characteristics of electro-hydraulic servo valve
根据以上额定条件建立的电液作动机构模型如图8 所示,其负载压差与电液伺服阀电流的压力增益特性仿真曲线如图9 所示。对比图5、图6 和图7、图9 可知,电液伺服阀模型[11-12]流量特性、压力特性吻合度较高,所建电液伺服阀模型较为准确。
其次根据变负载作动机构动力学分析式(8)考虑变负载模型。当活塞杆位移为0 时,气流通道全关,此时S1=1.21 m2;当活塞杆达到最大位移0.22 m时,气流通道全开,对应S1=0。可得作动杆在任意位置x时
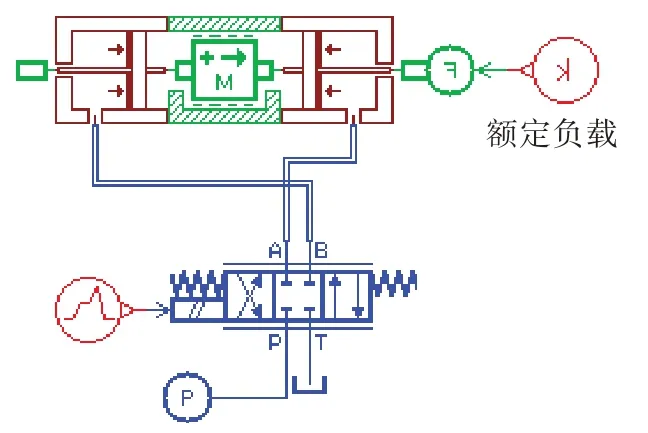
图8 额定条件下电液作动机构AMESim 模型Fig.8 AMESim model of electro-hydraulic actuation mechanism under rated condition
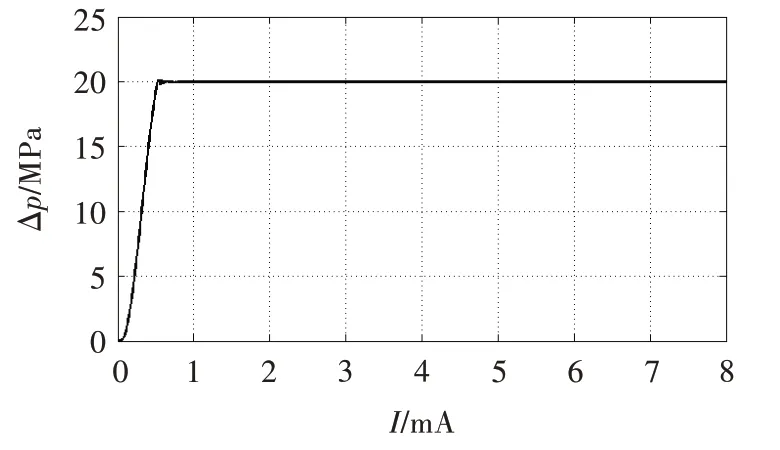
图9 额定负载下模型压力增益特性曲线Fig.9 Model pressure gain curve under rated load

由式(7)得到等效变负载力,考虑无级盘与中间壳体存在间隙,引入修正因子k对气动摩擦力矩进行修正,建立变负载液压作动筒模型(图10)。

图10 变负载液压作动机构AMESim 模型Fig.10 Variable load hydraulic actuator AMESim model
考虑液压泵站结构及上述方法,建立开环变负载电液作动机构非线性AMESim 模型(图11)。

图11 变负载电液作动机构非线性AMESim 模型Fig.11 Nonlinear AMESim model of electro-hydraulic actuator with variable load
4 变负载电液作动机构输入输出特性
在实际供油压力pS下,考虑负载压降pL时的负载流量[13]为:

式中:QN为电液伺服阀额定流量。
电液伺服阀动态特性[14-15]可用二阶振荡环节表示为:

式中:Kq为流量增益,ωsv为电液伺服阀固有频率,ξsv为电液伺服阀阻尼比。则带负载情况下,电液伺服阀随负载变化的流量增益为:

根据质量守恒,液压油单位时间内进入液压作动筒腔内的流量等于该腔体积的增加,经拉普拉斯变换可得:

式中:A为活塞有效作用面积。因此变负载电液作动机构输入输出特性可用传递函数表示:

由于活塞杆作动力为活塞两端压差作用的结果(F=pLA),则

5 系统仿真
5.1 开环条件下模型准确度对比验证
为验证模型的准确度,在高空台流量调节阀物理试验台上开展了相关试验。设置试验条件为:液压作动筒初始位置0.015 m,电液伺服阀控制电流信号为10 mA。对液压作动机构模型进行仿真,其位移输出响应与试验数据对比如图12 所示(图中试验曲线出现小台阶变化是由于数据采集系统的采样周期为0.1 s),最大相对误差不大于1.78%;等效气动负载变化仿真曲线如图13 所示。
5.2 闭环条件下变负载电液作动伺服系统性能仿真验证

图12 变负载下模型位移响应与试验数据对比曲线Fig.12 Comparison of model displacement response and experimental data under variable load

图13 等效气动负载变化曲线Fig.13 Equivalent pneumatic load change curve
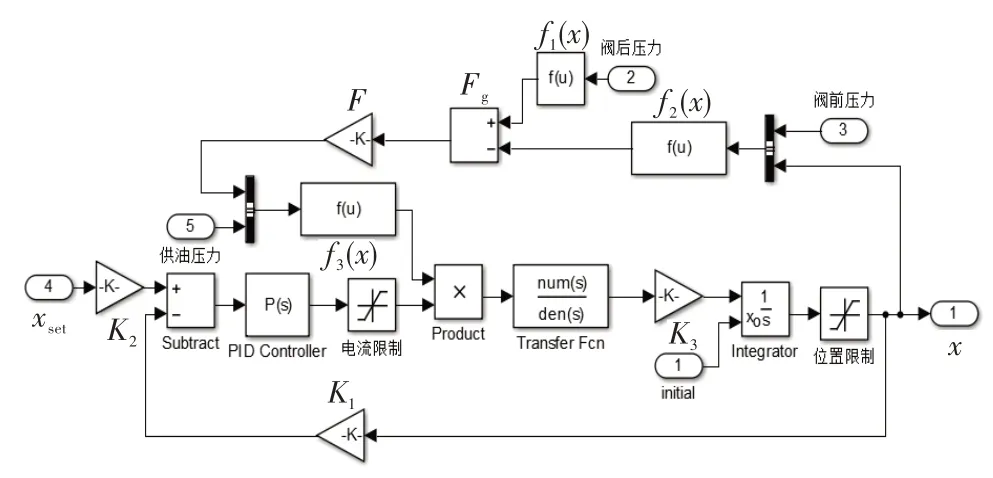
图14 闭环电液作动伺服系统Fig.14 Closed-loop electro-hydraulic servo system
根据式(15)变负载电液作动机构输入输出特性构建闭环伺服控制系统,如图14 所示。图中,K1及K2为位移信号转化为电流信号的单位转换系数。由于电液作动机构本身具有积分环节的作用,因此采用了文献[16-18]的标准结构方案,即控制器采用纯比例环节,并采用基于仿真结果数据对比的优化设计方法,设计的纯比例增益Kp=47.51。另外,考虑到电液伺服阀控制电流限幅及作动筒活塞杆限位,模型加入了电流限制和位置限制。
为了对上述方法设计的变负载电液作动伺服系统进行伺服性能和抗干扰性能验证,建立了带噪声气动压力变负载闭环电液伺服作动系统AMESim 仿真模型,如图15 所示。考虑到特种流量调节阀在实际工作中存在两种工况,为此根据这两种工况分别设计了仿真试验。
工况1:进气压力变化时,阀后压力在调节过程中保持恒定。设置仿真时间为10 s,阀前压力在第0~2 s 保持150 kPa 不变,在第2~6 s 由150 kPa 按线性衰减到120 kPa,在第6~10 s 保持120 kPa 不变,如图16(a)所示;同时,阀后压力在第0~10 s 保持100 kPa不变,如图16(b)所示。

图15 带噪声变负载闭环电液伺服作动系统AMESim仿真模型Fig.15 AMESim simulation model of variable load electro-hydraulic servo actuation system with noise

图16 工况1 下阀前阀后压力设置Fig.16 Pressure setting before and after valve under condition 1
液压作动机构位置指令按斜坡和正弦两种情况输入。斜坡指令在第0~2 s保持0 m 不变,在第2~7 s按线性增加到0.200 m,其后保持0.200 m不变;正弦指令在第0~10 s按y=0.05 sin(0.4πx)+0.150 变化。
在上述指令和带噪声阀前后压力同时加入情况下,电液作动机构的伺服性能和抗干扰性能的仿真结果如图17 所示。从图17(a)和图17(c)可得,模型在斜坡指令下的输出响应相对误差不大于1.20%,在正弦指令下的输出响应相对误差不大于1.30%,具有良好的伺服跟踪性能和抗干扰性能。从图17(b)和图17(d)可看出,作用在无级盘上的等效气动载荷随着作动筒活塞杆的运动而正相关变化,且变化范围中最大值与最小值的比值分别接近于5.6 和1.6,表明了该建模方法对于气动载荷变化大的流量调节阀电液伺服作动系统问题的有效性。
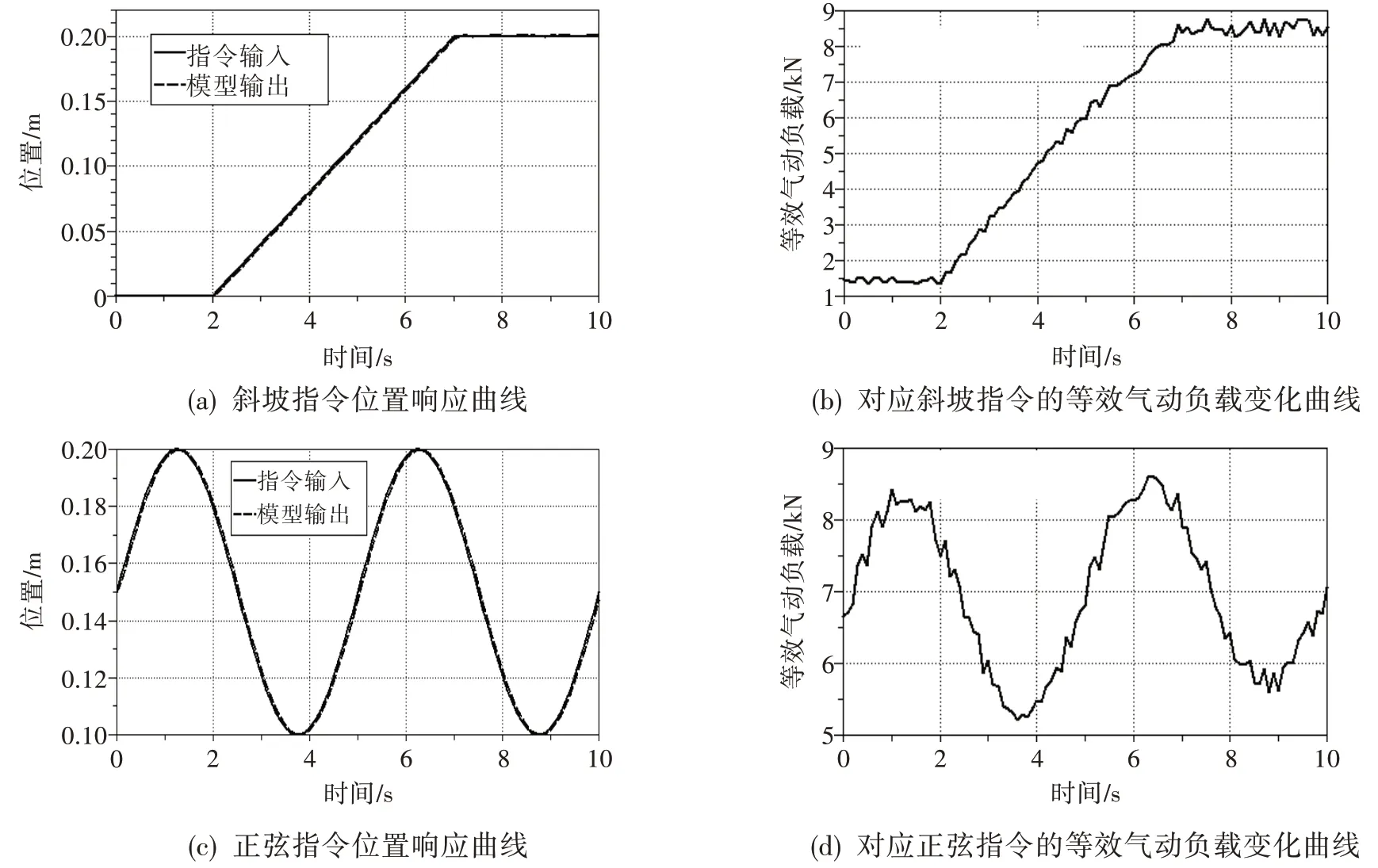
图17 工况1 下仿真结果Fig.17 Simulation results under condition 1
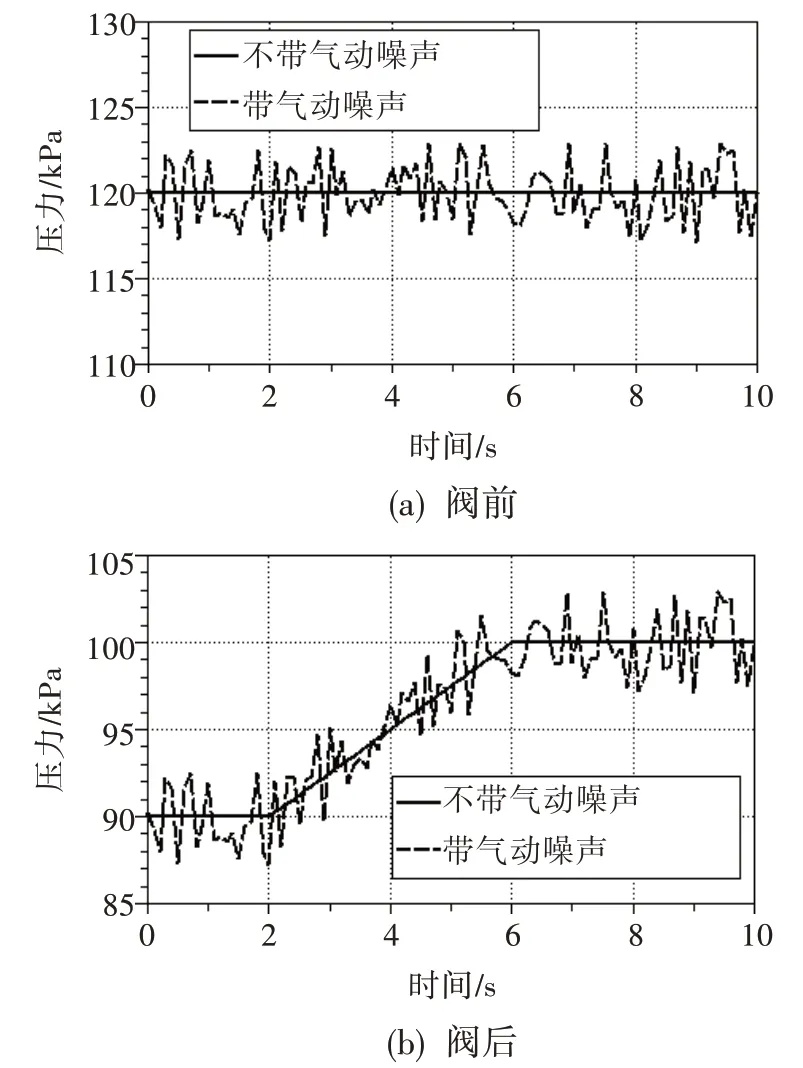
图18 工况2 下阀前阀后压力设置Fig.18 Pressure setting before and after valve under condition 2
工况2:进气压力保持恒定时,阀后压力随发动机进气压力变化。设置仿真时间为10 s,阀前压力在第0~10 s 保持120 kPa 不变,如图18(a)所示;同时,阀后压力在第0~2 s 保持90 kPa 不变,在第2~6 s 由90 kPa 按线性增大到100 kPa,在第6~10 s 保持100 kPa不变,如图18(b)所示。
加入与工况1 相同的斜坡和正弦指令,则在上述指令和带噪声阀前后压力同时加入情况下,电液作动机构的伺服性能和抗干扰性能仿真结果如图19 所示。从图19(a)和图19(c)可得,模型在斜坡指令下的输出响应相对误差不大于1.26%,在正弦指令下的输出响应相对误差不大于1.40%,具有良好的伺服跟踪性能和抗干扰性能。从图19(b)、图19(d)可看出,作用在无级盘上的等效气动载荷随着作动筒活塞杆的运动而正相关变化,且变化范围中最大值与最小值的比值分别接近于4.3 和1.6,表明了该方法能有效应用于气动载荷变化大的流量调节阀电液伺服作动系统建模问题。
6 结论
(1) 针对高空台全包线飞行环境模拟过程中流量调节阀气动负载变化大难以快速调节以伺服跟踪位置指令的问题,提出一种建立变负载电液作动机构模型的建模方法,提高了变负载流量调节阀的建模准确度。与试验数据对比,模型最大相对误差不大于1.78%。
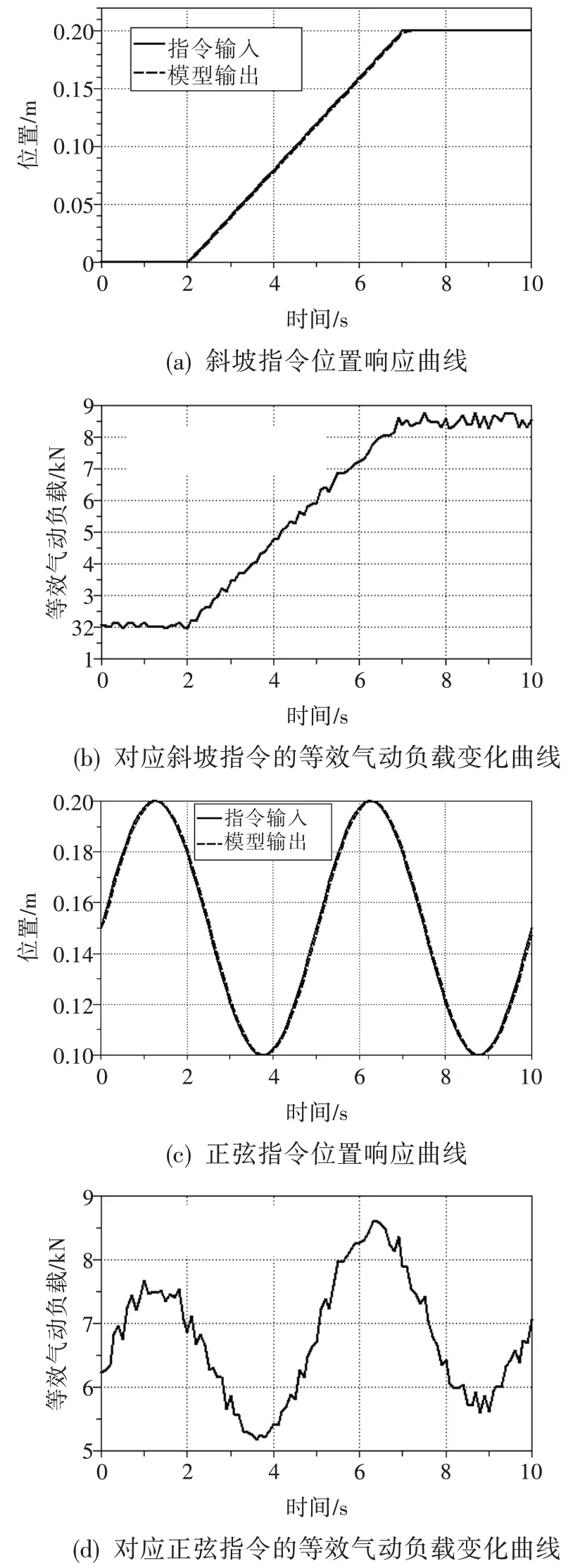
图19 工况2 下仿真结果Fig.19 Simulation results under condition 2
(2) 在阀前、阀后气动压力干扰情况下进行了闭环伺服性能仿真验证,其斜坡响应最大相对误差不大于1.26%,正弦响应最大相对误差不大于1.40%,具有良好的伺服跟踪性能和抗干扰性能。
