航空发动机多设计点热力循环分析方法的构建及应用
2019-11-22郑华雷王召广蔡建兵
郑华雷,王召广,蔡建兵,黄 兴
(中国航发湖南动力机械研究所,湖南株洲 412000)
1 引言
航空发动机热力循环分析确定了发动机的几何和全包线内的性能,是发动机设计过程中极为重要的一环。传统的单设计点热力循环分析方法(简称单设计点方法(SDP))是一个串行的过程,即先选取一个工作状态作为发动机的设计点进行热力循环分析,确定发动机在设计点的循环参数。一般情况下,设计点参数确定后,发动机的几何和全包线性能也随之确定[1-2],其设计域不受非设计点需求影响,很难满足所有状态的性能需求,需要反复调整、迭代设计点参数。如何选取和调整设计点热力循环参数,得到合适的设计域,需要设计人员对发动机工作特性有很深的理解,且带有很大的主观性,缺乏严格的数学判据。与之相对,多设计点热力循环分析方法(简称多设计点方法(MDP))是一个并行的过程,在热力循环分析之初便以多个典型工作状态作为设计点,所有设计点上的所有需求和限制都会影响设计域,设计域内的每一个点都严格满足所有工作状态的性能需求和使用限制。
鉴于多设计点方法的优势,国外研究人员开始利用多设计点思想进行航空发动机设计。Kestner等[3]采用多设计点思想研究了技术限制、构型对超大涵道比涡扇发动机性能的影响;Bellocq[4]、Perullo[5]、Hendricks[6]等研究了热力循环参数在不同工作状态下对桨扇发动机性能的影响;Lehmann[7]、Hughes[8]等开展了新一代通用核心机设计,使该通用核心机可满足不同构型发动机在不同工作状态下的性能需求;Schutte 等[9]把多设计点方法和环境设计空间(EDS)结合起来进行热力循环分析,使发动机能同时满足性能、使用限制及污染排放、噪声等要求。但上述研究仅提及多设计点方法的概念及应用效果,对如何构建、求解等实现多设计点方法的具体做法没有披露。
本文以大涵道比涡扇发动机热力循环分析为研究对象,提出一种多设计点热力循环分析的实现方法,并给出了详细的分析步骤和求解方法。同时,采用具体算例,对比了多设计点方法与单设计点方法的实现过程和得到的设计域,并对两设计域的差异进行了深入分析。
2 多设计点热力循环分析步骤
以大涵道比涡扇发动机为研究对象,阐述多设计点热力循环分析步骤。发动机各工作状态下的推力为必须满足的性能需求,以耗油率为一个优化目标(研究为单目标优化,不考虑质量、单位推力等因素)。发动机的技术限制由当前技术水平决定,一般情况下,压气机出口压力、温度,涡轮导叶、转子叶片的金属温度是较重要的技术限制[10-11]。本研究以高压涡轮导向器金属温度作为技术限制。
2.1 设计点设置
飞机方将根据爬升速率需求,在不同飞行高度、马赫数下对发动机提出推力要求。为简化分析,以爬升末端(TOC)状态替代整个爬升过程;根据起飞质量及滑跑距离,对发动机提出起飞推力要求。为保证热天的起飞推力,起飞状态(TO)定义为ISA+25 K;定义巡航状态(Cruise)的高度、速度及推力略小于爬升末端状态,巡航状态的耗油率为优化目标。此外,发动机还有一个最大连续(Max continuous)状态,以应对发动机失效。一般情况下,大涵道比涡扇发动机最大连续状态的推力等级与其起飞状态的一致,本文以起飞状态代替[12]。
MDP 方法选取所有典型工作状态作为设计点,再在这些设计点中选取一个气动设计点(ADP)。压气机、涡轮等部件由气动设计点的设计参数和特性图(与此部件相似的特性图或通用特性图)确定缩放因子,进而确定部件特性。通常,发动机在爬升末端状态时的换算流量、换算转速最大,该状态决定了发动机的最大尺寸。为此,选取爬升末端和起飞状态为设计点,爬升末端状态为气动设计点。
在发动机典型工作状态、性能需求和使用限制确定之后,需要把设计变量、性能需求和技术限制分配到相应的设计点。发动机模型的主要热力循环参数,有作为设计变量的燃烧室出口温度T4、外涵风扇压比πFⅡ、低压压气机(内涵风扇和增压级用一个特性图,在计算时看成低压压气机)压比πCL、高压压气机压比πCH、总压比πC、涵道比B,和不作为设计变量、根据经验和设计水平取值的压气机部件与涡轮部件的效率、燃烧室燃烧效率、燃烧室及通道的压力损失、转子机械效率等。
2.2 数学模型构建及求解
确立多设计点及对应的设计变量后,在所有设计点建立平衡方程并求解。公式(1)为平衡方程及与其对应的迭代变量。平衡方程和迭代变量分为两种类型,一种为设计人员根据性能需求、使用限制之间关系建立的平衡方程(User defined)及与其对应的迭代变量,另一种为使发动机各部件之间满足功率、流量平衡的平衡方程(Engine matching)及与其对应的迭代变量。
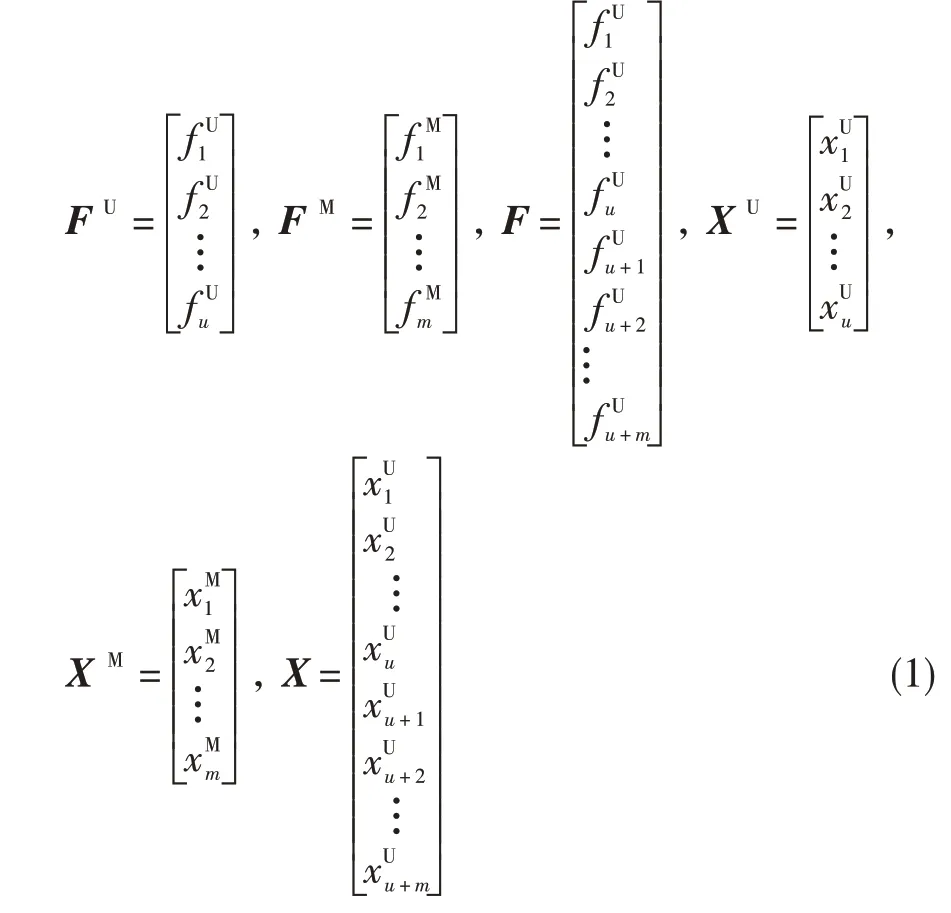
把所有设计点建立的平衡方程整合成一个非线性方程组FX=0 。非线性方程组包含了所有设计点的性能需求和使用限制的平衡方程、各设计点之间满足发动机部件共同工作的平衡方程,所得到的设计域必然严格满足发动机在各个工作状态的性能需求和使用限制。数学模型构建完成后,需求解非线性方程组。与普通求解不同,初始形成的非线性方程组的方程数有可能不等于迭代变量,求解器需要判断进行预处理,使方程数目与变量一致,然后进行求解。
3 具体算例的构建及结果分析
表1 列出了发动机的工作状态定义、性能需求和技术限制,其中H为飞行高度,Ma为飞行马赫数,T为环境温度,F为对发动机需求推力,THNGV为高压涡轮导向器金属温度。后文中的多设计点算例和单设计点算例,都必须满足此表给出的技术限制和性能需求。
3.1 多设计点方法设计点参数设置
表2 给出了多设计点方法算例的设计点参数设置。πFⅡ、πCL、πCH、πC、B为爬升末端状态的设计变量。其中,πFⅡ、πC分别为设计域的x变量和y变量,πFⅡ的取值范围为1.30~1.75,πC的取值范围为35~65;对于每一组πFⅡ和πC的循环参数,求解器通过寻优寻找最优涵道比,使巡航状态耗油率最低。根据当前技术水平起飞状态取T4=1 850 K;根据当前压气机和涡轮部件的设计水平,给出了压气机部件多变效率ηn,c和涡轮部件多变效率ηn,T,部件的等熵效率由多变效率和压比(膨胀比)计算得到。高压涡轮导向器金属温度,由燃气的温度与流量、冷却气体的温度与流量等气动参数计算得到,计算方法详见文献[13]。
表3、表4 列出了在两个设计点建立的平衡方程的迭代变量和平衡方程左、右两侧的取值。其中,W代表质量流量,nH和nL分别为高、低压轴转速,Wcool,HNGV代表高压涡轮导向器冷却气流量,R为部件特性图一参考值,求解器利用转速和R确定工作点在特性图上的位置。两个设计点共有10 个迭代变量,11个平衡方程,无法直接求解。这是因为相关高压涡轮导向器金属温度的平衡方程在两个设计点重复出现,而对应的迭代变量Wcool,HNGV只有一个,求解器需在求解过程中进行判断,对非线性方程组进行重构,只保留温度较高的平衡方程,最终形成10个平衡方程进行求解。

表3 爬升末端的平衡方程Table 3 Equilibrium equations at TOC
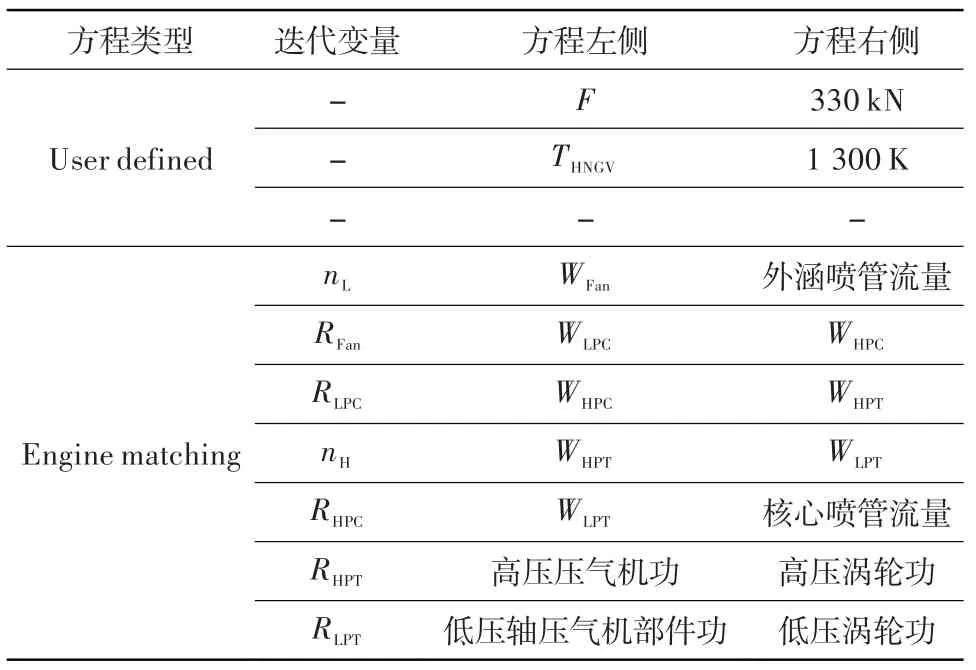
表4 起飞状态的平衡方程Table 4 Equilibrium equations at TO
3.2 单设计点方法设计点参数设置
表5 为单设计点方法算例1(SDP1)的设计点参数设置。为更好地比较多设计点方法和单设计点方法设计域的差异,在爬升末端状态,两种方法的πFⅡ与πC取值范围一致,πCL、B的计算方法一致,πCH、ηn,c和ηn,T取值一致,推力需求一致。单设计点方法在设计点计算之前假设了Wcool,HNGV和爬升状态的T4,且不随πFⅡ和πC变化,而在多设计点方法中这两个变量为迭代变量(表3)。
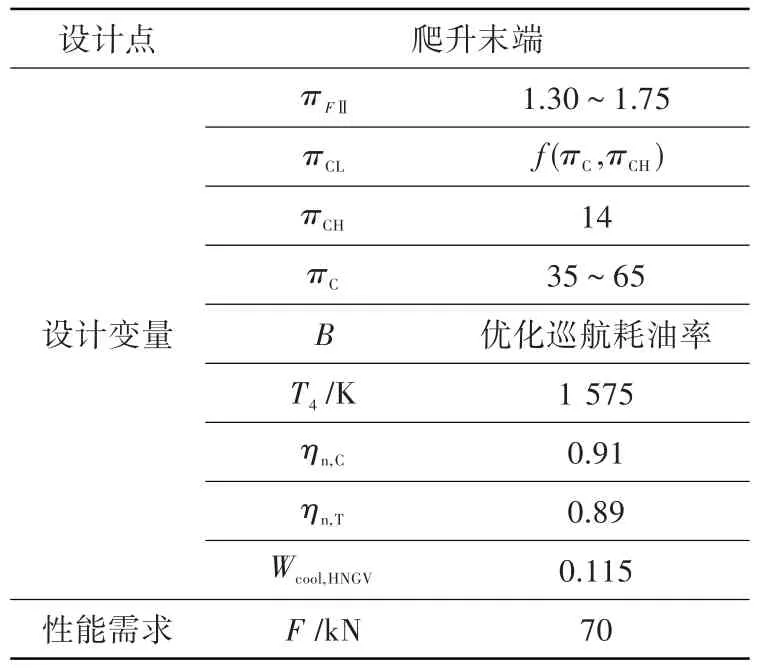
表5 单设计点方法算例1 的设计点参数设置Table 5 Parameters for SDP1 of single design point method
3.3 结果分析
对多设计点方法算例与单设计点方法算例设计域的不同之处进行了对比及原因分析,并比较了两种方法的优劣。图例中的πFⅡ和πC为爬升末端的设计变量,耗油率为巡航状态耗油率,推力为起飞状态推力,高压涡轮导向器金属温度为最高金属温度。
3.3.1 多设计点方法算例与单设计点方法算例1 设计域的对比
图1 为多设计点方法算例与单设计点方法算例1 的巡航耗油率对比。由图可知,多设计点方法算例耗油率随πC和πFⅡ的增加均为先减小后升高,存在一个最优的πC和πFⅡ组合使得发动机耗油率最低。单设计点方法算例1的耗油率随πC的增加同样为先减小后升高,但当πC在60~65范围内时耗油率的变化幅度很小。两种算例的设计域存在明显差别,最优耗油率及对应的πC和πFⅡ也不同。多设计点方法算例的耗油率最优结果0.055 5 kg/(h·N),πFⅡ=1.45,πC=50,B=10.2,对应的Wcool,HNGV=0.118,爬升末端T4=1 590 K。单设计点方法算例1 的耗油率最优结果0.055 3 kg/(h·N),πFⅡ=1.50,πC=63,B=9.1。如果不考虑技术限制,单设计点方法的优化结果更好。但实际上,由于单设计点方法的冷却气量和爬升末端T4不随πC和πFⅡ变化,这样会造成一部分设计域不满足要求。

图1 多设计点方法算例与单设计点方法算例1 的巡航耗油率对比Fig.1 Specific fuel consumption at cruise of MDP and SDP1
图2 为两种算例的起飞推力随πC和πFⅡ的变化。由图可知,多设计点方法算例的起飞推力保持为330 kN,而单设计点方法算例1 的起飞推力随πC和πFⅡ变化,变化范围为315~360 kN。发动机起飞状态的性能需求为推力330 kN,只有起飞推力大于330 kN 的区域才满足要求,即两个曲面的交线就是单设计点方法算例1 推力可行域的边界,推力在边界之下的区域为不可行域。

图2 多设计点方法算例和单设计点方法算例1 的起飞推力对比Fig.2 Thrust at TO of MDP and SDP1
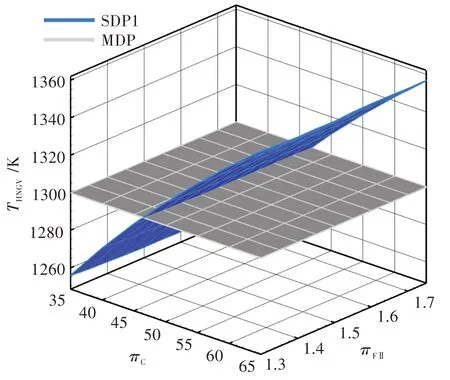
图3 多设计点方法算例和单设计点方法算例1 的高压涡轮导向器金属温度对比Fig.3 Metal temperature of high pressure turbine nozzle guide vane of MDP and SDP1
图3 为两种算法的高压涡轮导向器金属温度对比。类似于起飞推力,多设计点方法算例的高压涡轮导向器金属温度严格等于1 300 K,单设计点方法算例1 的高压涡轮导向器金属温度随πC的增加而升高,且变化范围为1 240~1 340 K。高压涡轮导向器最高允许金属温度为1 300 K,只有低于1 300 K 的区域才满足技术限制,即两个曲面的交线就是单设计点方法算例1 温度可行域的边界,在边界之上的区域为不可行域。
综合分析图2 和图3 可看出:多设计点方法的结果总是严格满足性能需求和技术限制;单设计点方法所得结果,在一部分区域由于推力大于指标要求或是高压涡轮导向器金属温度低于技术限制(使用了过多的冷气)造成了性能浪费,而另一部分区域由于不满足推力需求或是超出了高压涡轮导向器金属温度的技术限制造成了设计域的不可行。
在同时考虑性能需求和技术限制的条件下,图4 给出了单设计点方法算例1 设计域的可行域、温度边界和推力边界。由图可知:单设计点方法算例1的可行域只占其设计域的很小一部分,温度边界为πC≤45,推力边界与πFⅡ轴的交点为πFⅡ=1.45;耗油率最优点不在可行域内,不满足设计要求。可行域内的最优耗油率为0.055 9 kg/(h·N),πFⅡ=1.45,πC=45,B=11。
图5、图6 分别示出了多设计点方法算例的爬升末端T4和高压涡轮导向器冷却气量。由图可看出,爬升末端T4随πC和πFⅡ变化,且πFⅡ对爬升末端T4的影响较大,爬升末端T4随着πFⅡ的升高而降低。冷却气量也随πC和πFⅡ变化,且πC对冷却气量的影响较大,冷却气量随着πC的增加而增加。这是因为最高T4保持1 850 K 不变,随着πC的增加,压气机出口温度(冷气温度)增加,就必须增加冷却气量以保持高压涡轮导向器金属温度不变。
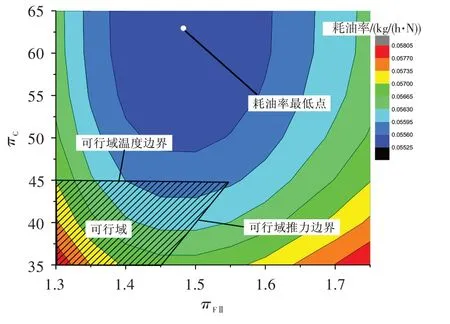
图4 单设计点方法算例1 的设计域和可行域Fig4 Design space and feasible region of SDP1
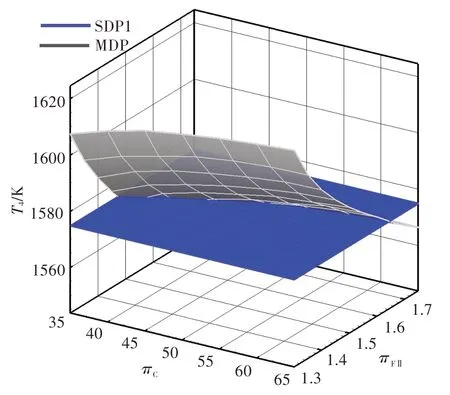
图5 多设计点方法算例的爬升末端燃烧室出口温度Fig.5 T4at TOC of MDP

图6 多设计点方法算例的高压涡轮导向器冷却气量Fig.6 High pressure turbine nozzle guide vane cooling flow of MDP
综上分析可知:单设计点方法假设了冷却气量和爬升末端T4保持不变,使设计域的一部分区域造成了性能浪费,而另一部分区域不满足要求,且性能最优点有可能在不可行域;多设计点方法的冷却气量和爬升末端T4为平衡方程组的迭代变量,随设计变量πC和πFⅡ变化,使得多设计点方法的设计域总是严格满足性能需求和技术限制。
3.3.2 单设计点方法设计参数的调整
单设计点方法算例1 的设计域存在很大一部分区域为不可行域,且耗油率最优点也在不可行域内,需要调整设计点参数以改变设计域边界。从前文分析可知,总压比增加使冷却气温度增加,必须增加冷却气量才能使高压涡轮导向器金属温度满足技术限制;随着风扇压比的增加,必须降低爬升末端T4才能使起飞推力满足性能需求。为此,在单设计点方法算例1 的基础上,单设计点方法算例2(SDP2)增加了冷却气量、降低了爬升末端T4(表6),以增加设计域的可行域,除此之外,两个算例的其他设置完全相同。
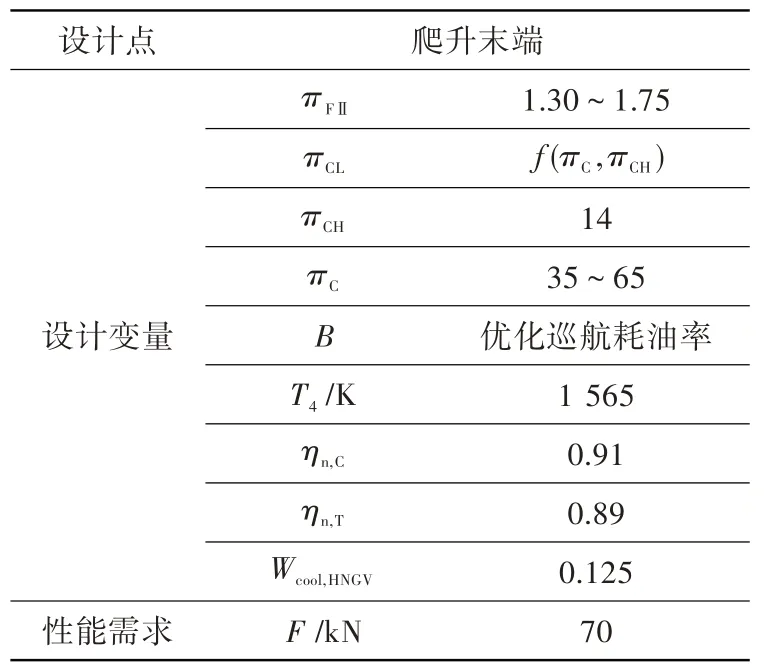
表6 单设计点方法算例2 的设计点参数设置Table 6 Parameters for SDP2 of single design point method
图7、图8 分别为多设计点方法算例与单设计点方法算例的起飞推力和高压涡轮导向器金属温度的对比。由图可知,单设计点方法算例2 的推力比单设计点方法算例1 的高,金属温度则比单设计点方法算例1 的低。这表明增大冷却气量并减小爬升末端T4,可以增加设计域的可行域范围。
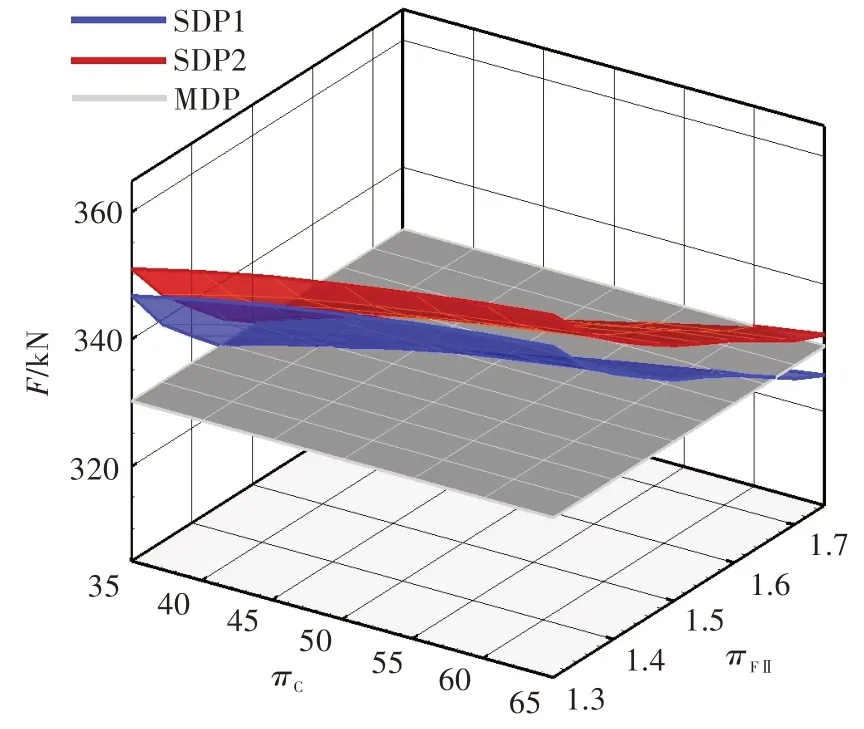
图7 多设计点方法算例和单设计点方法算例的起飞推力对比Fig.7 Thrust at TO of MDP,SDP1,SDP2
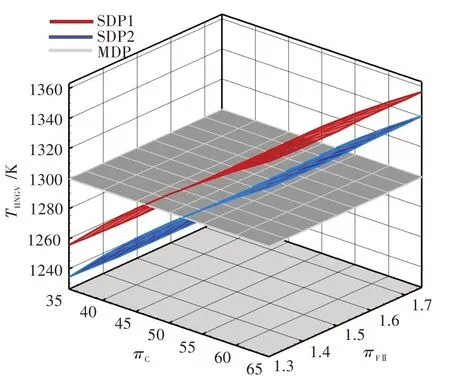
图8 多设计点方法算例和单设计点方法算例的高压涡轮导向器金属温度的对比Fig.8 High pressure turbine nozzle guide vane metal temperature of MDP,SDP1,SDP2
图9 为多设计点方法算例和单设计点方法算例的巡航耗油率对比。从图中可看出,多设计点方法算例和单设计点方法算例1、算例2 的设计域分别相交,但单设计点方法算例1 和算例2 并没有交线。对应于每个πC和πFⅡ的组合,单设计点方法算例2 的耗油率都比单设计点方法算例1 的高。
图10 示出了单设计点方法算例2 设计域的可行域。对比图4 可看出,单设计点方法算例2 的可行域明显增大,温度边界为πC≤50,推力边界与πFⅡ轴的交点为πFⅡ=1.5,但耗油率最优点依然不在可行域内。
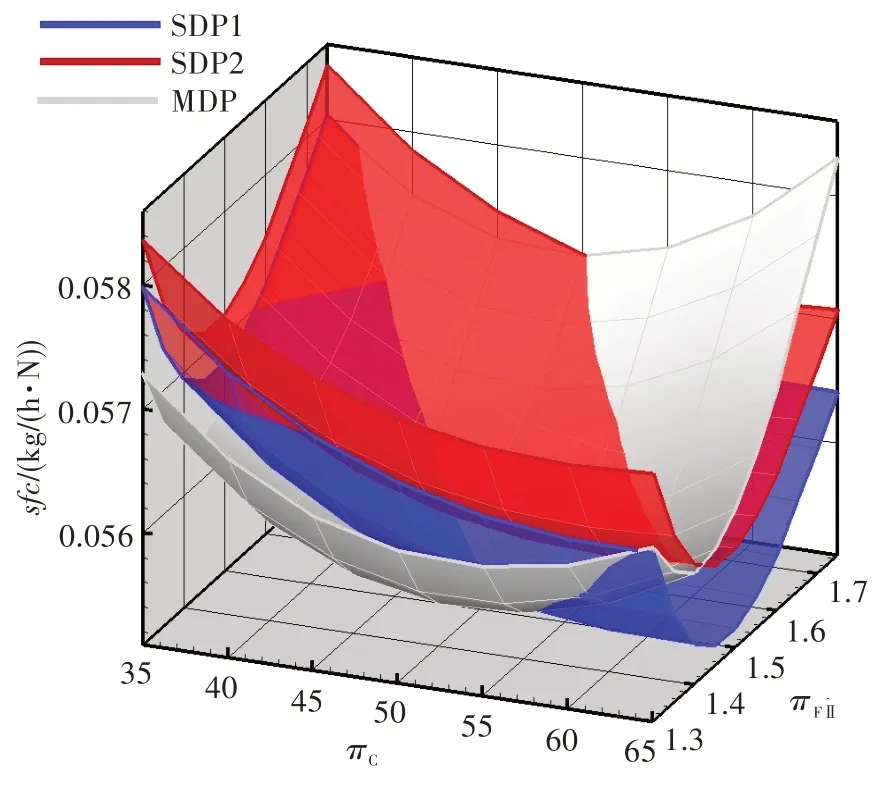
图9 多设计点方法算例和单设计点方法算例的巡航耗油率对比Fig.9 Specific fuel consumption at cruise of MDP,SDP1,SDP2

图10 单设计点方法算例2 的设计域及可行域Fig.10 Design space and feasible region of SDP2
综合分析图9、图10 可知:单设计点方法算例2由于降低了爬升末端的T4,增加了冷却气量,使得起飞推力比单设计点方法算例1 的大,高压涡轮导向器金属温度比单设计点方法算例1 的低,可行域范围增大;但是也由于冷气量的增加,在增大可行域范围的同时,使得巡航耗油率整体升高,最优耗油率约为0.551 kg/(h·N),优化结果反而变差,此时单设计点方法算例2 的耗油率最优点仍不在可行域内,若继续增大其可行域的边界,可以预见优化结果会继续恶化;如果减小冷却气量使耗油率整体降低,又会使可行域范围减小。由此看出,在单设计点方法中,仅通过设计人员主观调整,很难使设计域既满足所有技术限制和性能需求,又不造成性能浪费。
4 结论
针对航空发动机的热力循环分析过程提出了一种同时考虑多个设计点需求的实现方法,并详细介绍了其构建、求解过程。通过对比、分析表明,多设计点方法可以自动调整循环参数(文中为爬升末端燃烧室出口温度和高压涡轮导向器冷却气流量),使设计域总是满足技术限制和性能需求,确保航空发动机热力循环分析过程更为准确、高效。
