基于试验数据统计的畸变特性关联模型
2019-11-22吴森林刘晓晨王迎国
吴森林,叶 巍,张 毅,刘晓晨,王迎国
(中国航发四川燃气涡轮研究院,四川绵阳 621010)
1 引言
发动机气动稳定性评定是进气道与发动机相容性评定中最核心的内容,规范发动机稳定性设计与评定是发动机研制过程中不可回避的关键问题。针对该关键问题,国内外航空技术人员开展了大量进气畸变对发动机气动稳定性影响的研究,并建立了具体的评定方法和标准,如SAE ARP-1420、SAE AIR-1429、GJB/Z64 等。但由于所使用的理论分析方法还不够完善,迄今为止主要还是依靠试验验证手段来完成对发动机气动稳定性的评定。而压气机作为航空发动机的核心部件之一,其气动稳定性直接关系到发动机的工作状态,因此,在航空发动机研制过程中,压气机的气动稳定性评定被定为必不可少的试验科目之一。目前国外采用的发动机压气机稳定性评定试验方法,主要有英、美等国采用的模拟板和模拟网试验方法[1-2],以及俄罗斯采用的固定式插板试验方法[3-5]。
采用固定式插板方法进行发动机压气机气动稳定性检验,可以在压气机进口产生稳态压力畸变流场以及表现为频率和振幅随机变化的“紊流”畸变流场。这两种畸变共同影响压气机工作的稳定性。当综合畸变指数达到一定数值(一般为3%~10%)时,才能有效地评定压气机的抗畸变能力。不同压气机的进口气流速度不同,其固定式插板的深度和安装位置就不同。为了达到一定的畸变指数,在制定畸变试验方案时,一般需要加工4 组插入深度的插板和3 组安装距离的进气道,试验过程也需试着安装2~4 组插板和2~3 组安装距离[6-8],并进行多次试验。这样既提高了试验成本,又增加了试验风险。对试验数据进行统计后发现,在某一固定插板深度下,畸变指数随进口气流马赫数呈单值递增函数变化[9-11]。本文利用这一规律,对单位已有的压缩部件试验数据进行了整理分析,获取了不完全统计规律下的关联模型,并将该模型成功应用于压缩部件进气畸变试验方案制定中,可降低试验成本、提高试验效率。
2 试验数据统计及处理
2.1 数据统计
共收集整理了6 台份风扇/压气机畸变试验数据,表1 给出了各台份在设计点附近的进口马赫数(Ma)和进气道直径(D)。可以看出,压气机设计点的流速在0.13~0.50 马赫范围,进气道直径在200~850 mm 之间,包含了当前大多数风扇/压气机的进气流速范围,基本可以表征风扇/压气机进气畸变的强度特性。
2.2 数据处理
(1) 综合畸变指数相对偏差
综合畸变指数相对偏差为本文建立的关联模型与试验获取的综合畸变指数之间的偏差大小,表征了关联模型对畸变指数预测的准确性。

式中:ΔWx为综合畸变指数相对偏差,Wj为采用关联模型计算得到的综合畸变指数,W为试验中获取的综合畸变指数。
(2) 进口马赫数
为将不同状态畸变特性统一到一个基准上进行对比分析,本文定义了进口马赫数Ma(为插板前未受到扰动的均匀气流速度,即插板前来流马赫数)。可通过公式(2)计算得到流量函数q(λ),再查表得到Ma。

式中:G为流量管上测取的进口物理流量,T*为稳压箱内测取的进气总温,p*为稳压箱内测取的进气总压,A为进气道面积。
2.3 统计原则
分别整理统计了5 组插板深度(H)下,5 组气动界面与插板距离(L,下面简称安装距离)的畸变数据,如表2 所示。

表2 畸变发生器的布置状态Table 2 Position conditions of distortion generators
基于数据量限制,为使拟合曲线的马赫数范围更大,将L=2.95D、3.11D的数据近似为3.00D(前期的数据统计发现,L=2.95D、3.11D与L=3.00D的周向畸变指数变化均在测试误差范围内),将L=2.06D、2.20D的数据近似为2.00D。数据拟合过程中,考虑到马赫数等于零时流场不存在畸变,此时畸变指数理论上应为零,因此曲线拟合时采用过零点拟合。
3 数据分析
3.1 进气道直径对畸变特性的影响
在上述所统计的试验数据中,进气道直径从200 mm 到850 mm 不等,为明确进气道直径对畸变特性的影响程度,本文对不同进气道直径(750 mm和801 mm)下的插板吹风试验数据进行了对比。从图1 可以看出,在插板深度相同时,不同进气道直径之间的总压恢复系数和周向畸变指数随马赫数的变化曲线重合性均相当好,总压恢复系数最大偏差约为1.0%,周向畸变指数最大偏差约为0.2%,均在测试误差范围内。据此可认为,进气道直径对畸变特性的影响可忽略,后续统计规律中不再考虑进气道直径的影响。
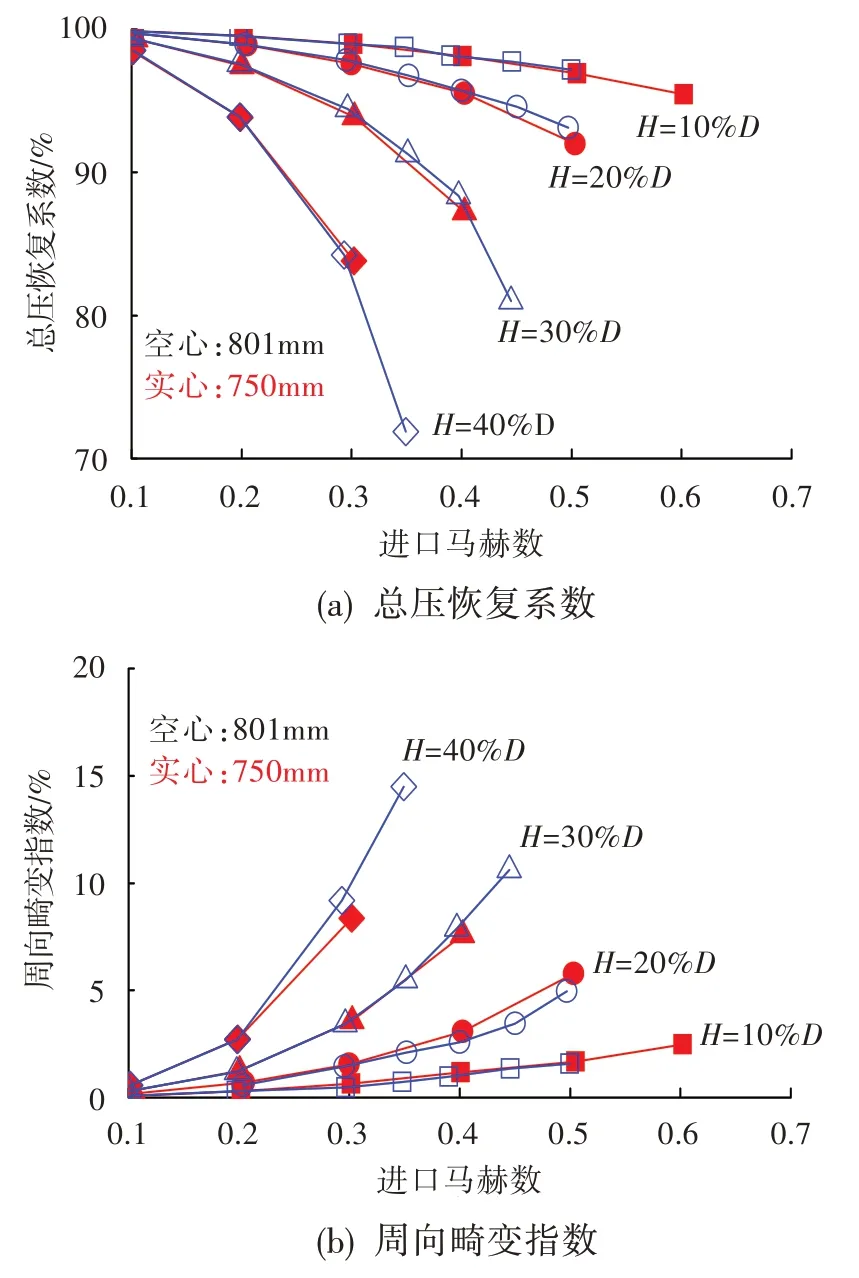
图1 不同进气道直径下的畸变流场特性对比Fig.1 Comparison of distortion flow field at different flow channel diameters
3.2 畸变指数关联模型
3.2.1 模型的建立
通过对上述6 台份压气机10 种畸变发生器布局方案试验数据进行整理分析,将各状态的综合畸变指数随马赫数变化的离散点进行对比(图2)可以发现,同一种畸变发生器布局方案下,综合畸变指数随马赫数的线性分布趋势非常好。根据离散点的分布规律,分别采用了2、3、4、5、6 阶次进行多项式拟合,发现当拟合阶次高于4 次方后容易导致低马赫数下畸变指数为负值,因此本文采用3 次方进行拟合。图3 给出了各状态下综合畸变指数随马赫数的关联模型。图中,虚线为通过关联模型外插部分,实线为试验数据拟合部分。
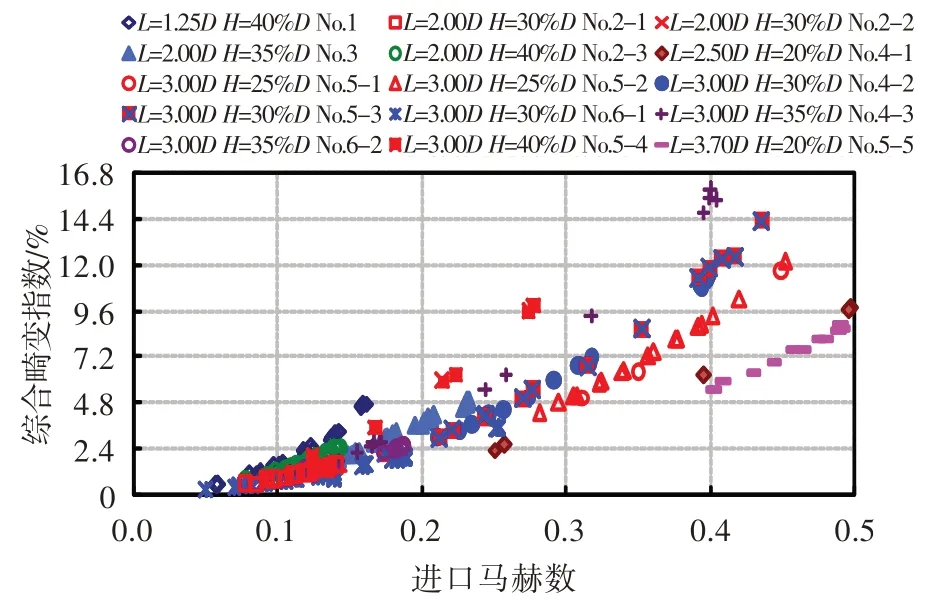
图2 综合畸变指数随进口马赫数的离散点Fig.2 The discrete points of comprehensive distortion index along with inlet Mach number
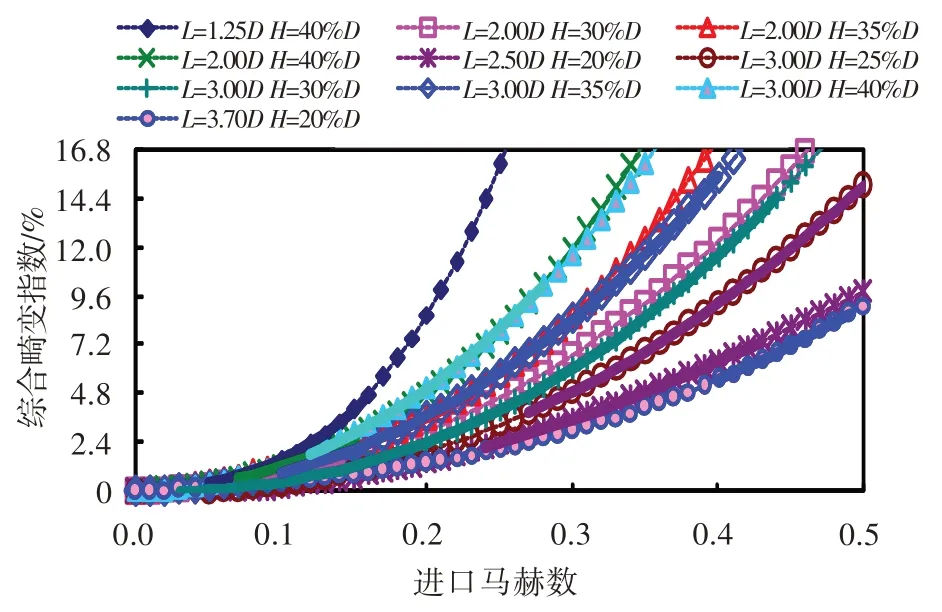
图3 综合畸变指数随进口马赫数的关联特性Fig.3 Correlation characteristics of comprehensive distortion index along with inlet Mach number
结合图3 和表2 可以看出,状态②与⑦、③与⑧、④与⑨、⑤与⑩的关联模型差异较小,状态①与其相同插板深度的关联模型差异明显。但整体上讲,同一插板深度下不同安装距离的综合畸变指数差异较小,而同一安装距离下不同插板深度的综合畸变指数差异较大。这说明,相比于安装距离,调整插板深度更容易改变进气畸变流场。

图4 综合畸变指数关联模型预测偏差Fig.4 Relative deviation caused by correlation model of comprehensive distortion index
为验证图3 中各关联模型对综合畸变指数预测的准确性,图4 给出了全部压气机性能试验获取的综合畸变指数与相对应的关联模型之间的偏差统计。可以发现,在0.2 马赫数以下有少部分离散点相对偏差超过了25.0%,整个马赫数范围绝大部分离散点的相对偏差处于14.0%范围内。从图5 也可以看出,相对偏差大于14.0%的离散点数目只占所有统计离散点总数的13.7%。由此可说明,本文建立的关联模型,在所拟合的马赫数范围内可以用于指导压缩部件进气畸变试验插板布局方案的制定,但在拟合的马赫数范围外仍需要进一步验证。
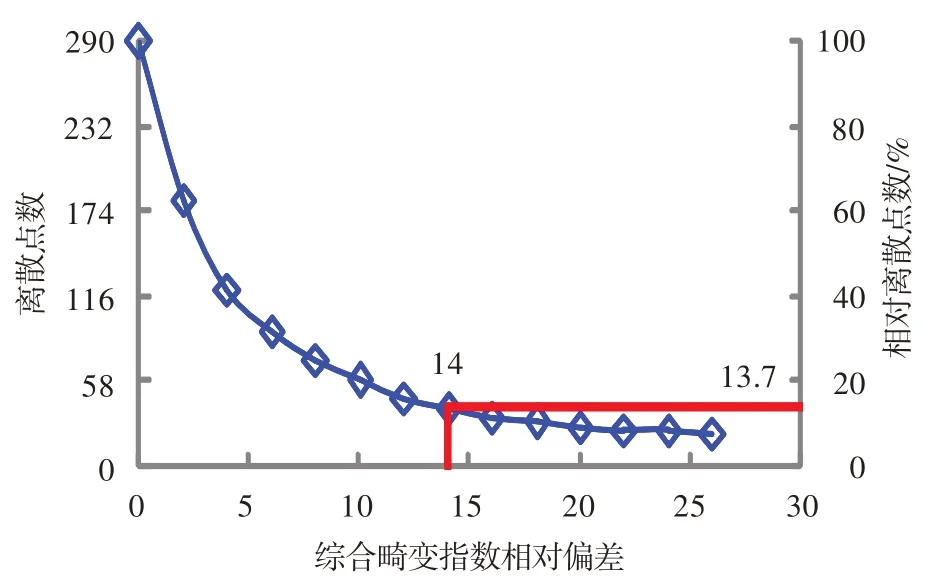
图5 预测偏差与离散点数目的关系Fig.5 Relation of predicted deviation and the number of discrete points
3.2.2 模型的工程应用
在多台份压缩部件进气畸变试验方案制定中对关联模型进行了应用验证。从图6 中关联模型应用前后试验效率的对比结果可以看出,模型建立前,插板深度需要使用2~4 组,插板安装距离分别要使用2~3 组,需要3~6 次试验才能完成预定试验内容;应用模型后,只需要1 组插板和1 组安装距离,开展1~2 次试验即可完成预定试验内容,试验效率提升了1 倍。另外,在某风扇畸变试验中,应用关联模型所预测的综合畸变指数与实测值的相对偏差不到10.0%,也进一步验证了模型的准确性。

图6 模型应用前后试验效率对比Fig.6 Comparison of test efficiency before and after model application
3.3 稳动态畸变指数占比统计
在压气机进气畸变试验中,用于评定压气机抗畸变能力的参数有综合畸变指数和稳定裕度损失,其中综合畸变指数为周向畸变指数与紊流度之和。由于紊流度属于动态参数,受白噪声、滤波结构形式、采样频率、采样周期等因素影响,其测试误差一般较大。为了在数据处理过程中判断紊流度的有效性,图7 给出了周向畸变指数在综合畸变指数中所占的百分比统计。从图中可看出,所统计的状态点中,周向畸变指数在综合畸变指数中的比例基本处于40%~60%区间。根据综合畸变指数公式可以推出,紊流度在综合畸变指数中所占的比例为40%~60%,考虑到±10%的畸变流场压力测试精度,可认为周向畸变指数约等于紊流度。据此,当压气机由于结构原因无法布置动态总压测点时,可用两倍周向畸变指数的方式近似得到综合畸变指数,进而评定压气机的抗畸变敏感性;同时,还可利用这一结论判别紊流度的粗大误差。
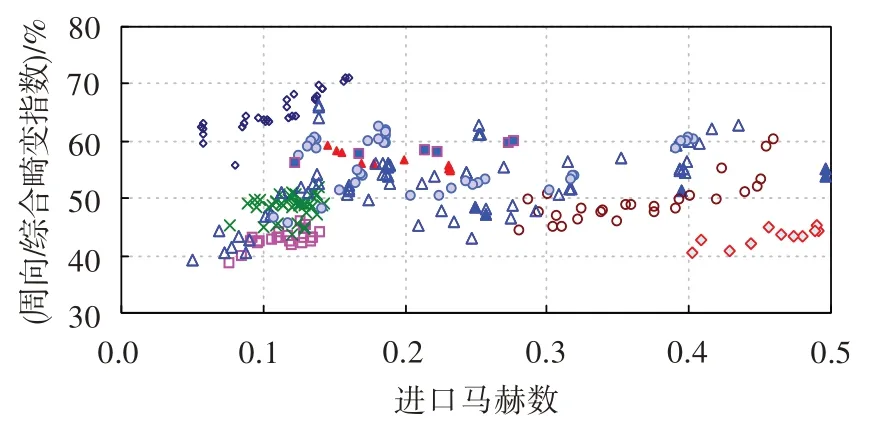
图7 周向畸变指数在综合畸变指数中所占比例Fig.7 The proportion of circumferential distortion index in comprehensive distortion index
4 结论
(1) 进气道直径大小对畸变特性基本无影响,可忽略。
(2) 建立了基于试验数据不完全统计规律下畸变指数与插板几何特性的关联模型。该模型已用于指导压缩部件进气畸变试验方案的制定,并将试验效率提升了1 倍。试验过程中,当需要调整压气机进口畸变强度时,采用更换插板深度的方式比改变距离更容易达到目的。
(3) 周向畸变指数在综合畸变指数中的占比为50%±10%,当压气机由于结构原因无法布置动态总压测点时,可用两倍周向畸变指数的方式近似得到综合畸变指数。
(4) 由于数据有限,本文所建立的综合畸变指数与进口马赫数的关联模型还存在很宽的区域(图3中的虚线)需要验证,在以后工作中应使用更多的试验数据对各关联模型进行修正完善。
