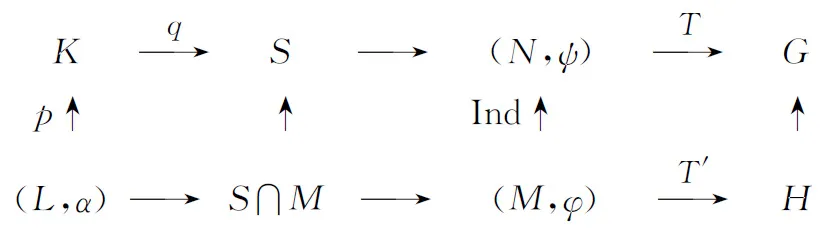特征标的诱导源与复合Clifford对应

2019-11-21靳平温馨

山西大学学报（自然科学版） 2019年4期

靳平，温馨

(山西大学数学科学学院,山西太原 030006)

0 引言

在有限群的表示论中,研究子群和群本身的特征标理论之间的相关影响,特别是描述和控制特征标的诱导现象,始终是非常活跃的核心课题之一。在此出现了两个相互对偶的重要问题:其一,子群的特征标如何决定群本身的特征标;其二,群本身的特征标如何从子群诱导。详言之,设G为任意有限群,H≤G为G的一个子群,任取θ∈Irr(H)为H的一个不可约复特征标，则θ所能影响到的群G的不可约特征标，最主要也是最自然的即为θ到G的诱导θG。其所有不可约分量，记为Irr(G|θ)，称为G的所有在θ上方的不可约特征标。反之,任取χ∈Irr(G),研究χ的所有诱导过程,即考察诱导χ所有的特征标对(A,α)，其中A≤G，而α∈Irr(A)满足αG=χ,寻找和刻画诱导过程的不变量,并设法获得某种共轭唯一性,均为特征标理论中的基本研究课题。

一般而言研究子群H的不可约特征标θ在群G上方的不可约特征标的集合Irr(G|θ)是非常困难的，甚至是关于该集合的元素个数|Irr(G|θ)|迄今为止尚未找到计算公式。然而当H为G的正规子群时，按惯例改记H为N,则著名的Clifford对应断言特征标的诱导为双射:

据此可将θ在G上方的不可约特征标集合Irr(G|θ)的研究归结为其在稳定子Gθ上方的不可约特征标集合Irr(Gθ|θ)。但θ是Gθ-不变的,故(Gθ,N,θ)为Isaacs意义下的一个特征标三元组。因为关于特征标三元组的研究，目前已有很多的研究手段,例如射影表示理论和特征标三元组同构等技术,并取得了深刻而丰富的成果,所以,正规子群上方的特征标理论,可以被认为是研究的较为深入和令人满意的。关于Clifford理论可参考[1-4]。

对非正规子群H而言,为了模拟正规子群N上方的Clifford对应,Dade在[5]中引入了诱导源的概念。称G的一个特征标对(H,θ)为G的一个诱导源,如果公式(1)成立,即特征标的诱导给出了从Irr(Gθ|θ)到Irr(G|θ)的一个对应。相关的概念和符号含义,可见本文下一节。注意到H◁Gθ，故(Gθ,H,θ)恰为一个特征标三元组,按上述说明,则诱导源(H,θ)上方的特征标理论亦可被视为比较好研究的。

事实上,诱导源为特征标理论的发展提供了一种强有力的技术,可用来研究很多重要的特征标猜想和问题。Dade在[1]中首先研究了群G的所有诱导源构成的集合IS(G),在此最为基本的问题是诱导源的判别。在2004年Isaacs和Lewis发现了诱导源的共轭稳定性,从而解决了次正规诱导源的判别问题,即[6]中定理A和定理B。在2006年Lewis在研究M-群的正规结构时,给出了特征标对是诱导源的一个充分条件,见[7]中引理3.7。此外,Loukaki在[8]和[9]中也大量使用了诱导源的观点和技术,并且和Dade合作在[10]中系统地发展了线性极限理论,其中出现的特征标对应均为诱导源对应。相关研究可以参考[11-15]。

本文首先研究诱导源的判别问题。我们在诱导源共轭稳定性的基础上,建立了一个惯性群引理,即下述引理3,据此获得了关于诱导源的更多判别条件,其意义和价值在于补充和加强了Dade的诱导源判别定理(见[5]中定理3.1)。以下是本文第一个主要结果,详细内容及符号说明见本文定理1。

定理A设G为有限群,(A,α)∈IS(G)为G的诱导源。如果(A,α)≤(H,θ)≤G,则(H,θ)也是G的诱导源当且仅当下述等价条件之一成立:

(1)(Hα,θα)∈IS(Gα)且Gα(θα)≤NG(H).

(2)(Hα,θα)∈IS(Gα)且G(α,θ)=G(θα).

(3)(Hα,θα)∈IS(G)且G(α,θ)=G(θα).

(4)Ind:Irr(G(α,θ)|θα)→Irr(G|θα)为双射。

其次,我们将研究诱导源对应。根据Dade在[5]中引入的术语,如果(A,α)∈IS(G),即(A,α)为G的一个诱导源,对G的任意一个特征标对(H,θ),按定理A中的记法,Dade称(Hα,θα)为(H,θ)的一个诱导源对应。最为重要的情形是(H,θ)亦为G的诱导源,类似于上述提及的Clifford理论,此时关于(H,θ)的研究亦可归结为G=Gθ的情形,亦即H◁G且θ∈Irr(H)为G-不变的。按惯例,我们改记正规子群H为N,称T=(G,N,θ)为一个特征标三元组。在此环境中,使用我们的惯性群引理3和上述定理A,不难验证一个特征标对(M,φ)为(N,θ)的诱导源对应当且仅当NG(φ)=G,N∩G(φ)=M,并且φN=θ。显然M◁G(φ),故得到一个新的特征标三元组(G(φ),M,φ)。方便起见,我们可将特征标对的诱导源对应等价地定义为特征标三元组的诱导源对应:设T=(G,N,θ)和R=(H,M,φ)均为特征标三元组,如果满足G=NH和M=N∩H,并且φ在θ的下方,则称R为T的一个子特征标三元组,记为R≤T。进而,如果还有φN=θ,则称R为T的一个诱导源对应。按Dade的符号,特征标三元组T的所有诱导源对应记为ISC(T)。值得指出的是,Dade所定义的特征标三元组的诱导源对应,即等同于Isaacs在[16]中定义的特征标三元组的诱导子可以参看[17-18]。

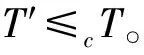
关于特征标三元组的诱导源对应和复合Clifford对应,Dade在[5]中的主要结果,即定理6.5,证明了当N为奇数阶群时,则ISC(T)=CCC(T)。该定理将诱导源对应分解为若干Clifford对应的合成,被公认为是一个深刻的结果,具有广泛的应用。值得指出的是其证明非常艰难,长达8页的篇幅,特别是还使用了在[19]中关于双曲模的深刻定理,故非纯特征标的证明。

本文第二个主要结果即给出了Dade上述定理的一个新的纯特征标的简化证明,特别是得到了该定理的一个加强和推广,这在应用时将获得技术上的改进。

定理B 设T=(G,N,ψ)为一个特征标三元组,如果N为可解群,并且ψ(1)为奇数,则T的诱导源对应等同于其复合Clifford对应,即ISC(T)=CCC(T).

我们将使用Isaacs的经典教材[23]中的符号和术语,只讨论有限群的复特征标。按Dade在[10]中的记法,用G′表示另外一个任意群,而不是G的导群。

1 诱导源及其判别

我们先定义特征标对及其稳定子。设H≤G是群G的子群,对任意θ∈Irr(H),则称(H,θ)为G的一个特征标对,记作(H,θ)≤G。任取g∈G,定义θ的共轭特征标θg∈Irr(Hg)为θg(hg)=θ(h),对任意h∈H,则G共轭作用在其所有的特征标对的集合上,记(H,θ)在G中的稳定子为Gθ或G(θ),即

Gθ={g∈G|(H,θ)g=(Hg,θg)=(H,θ)} .

在文献中亦称Gθ为(H,θ)在G中的惯性群,记为IG(θ)。特别地,当H≤G是G的正规子群时,我们称(H,θ)为G的一个正规特征标对,记作(H,θ)◁G,此时G(θ)=IG(θ)即为通常的惯性群。此外,如果(K,ψ)也是G的特征标对,使得H≤K且θ在ψ下方,则记为(H,θ)≤(K,ψ).

定义1 设G为群,(H,θ)≤G为一个特征标对,如果特征标的诱导Ind:Irr(Gθ|θ)→Irr(G|θ)为双射,则称(H,θ)为G的一个诱导源。群G的所有诱导源的集合记为IS(G)。

下面是诱导源的两个最为基本的性质,证明见[5]中定理2.8。

引理1设(H,θ)≤K≤G,则下述成立。

(1)如果(H,θ)∈IS(G),则(H,θ)∈IS(K).

(2)如果Ind:Irr(K|θ)→Irr(G|θ)为双射且K≤G(θ),则K=G(θ),从而(H,θ)∈IS(G).

以下是Isaacs和Lewis在2004年发现的诱导源重要性质,即[6]中的定理A和定理B。

引理2如果(H,θ)∈IS(G),则(H,θ)在G中是共轭稳定的,即对任意g∈G和(K,ψ)≤G,只要(H,θ),(H,θ)g≤(K,ψ),就有某个k∈K使得(H,θ)g=(H,θ)k.

在上述两个引理的基础上,我们获得了关于特征标对的稳定子或称惯性群的一个基本引理。

引理3设(H,θ)≤(K,ψ)≤G,并且(H,θ)∈IS(G),则下述成立。

(1)G(ψ)=G(θ)K.

(2)G(ψ,θ)⊆G(ψθ)⊆G(θ).特别地,当(K,ψ)∈IS(G)时,G(ψ,θ)=G(ψθ).

(3)G(ψ)=G(ψ,θ)K.

相应的惯性群图表如图1所示。

证明(1)任取g∈G(ψ),则(K,ψ)g=(K,ψ),故(H,θ),(H,θ)g≤(K,ψ)。根据诱导源的共轭稳定性,可知存在k∈K使得(H,θ)=(H,θ)gk,即gk∈G(θ),表明G(ψ)=G(θ)K.

Fig.1 Stabilizer group

图1 惯性群

(2)按定义G(ψ,θ)=Gψ∩Gθ,即固定θ与ψ的群元素必然固定(Kθ,ψθ),故G(ψ,θ)⊆G(ψθ)。又因为(H,θ)∈IS(G)和(H,θ)≤(Kθ,ψθ)≤G,应用(1)知G(ψθ)⊆GθKθ=Gθ.

(3)从(1)可知G(ψ)=G(ψ)∩(G(θ)K)=G(ψ,θ)K.

有了上述准备,现在可证明本文第一个主要结果,即引言中定理A。

定理1设(A,α)≤(H,θ)≤G,如果(A,α)∈IS(G),则下述等价:

(1)(H,θ)∈IS(G).

(2)(Hα,θα)∈IS(Gα)且Gα(θα)≤NG(H).

(3)(Hα,θα)∈IS(Gα)且G(α,θ)=G(θα).

(4)(Hα,θα)∈IS(G)且G(α,θ)=G(θα).

(5)Ind:Irr(G(α,θ)|θα)→Irr(G|θα)为双射。

证明(1)⟹(2)。根据引理1,从(A,α)∈IS(G)可知(A,α)∈IS(Gθ),已知(H,θ)∈IS(G),故

Ind:Irr(Gθ(α)|α)→Irr(Gθ|α)和Ind:Irr(Gθ|θ)→Irr(G|θ).

(2)⟹(3)。因为Gα(θα)正规化H,所以Gα(θα)=G(θα)≤NG(H),从而G(θα)=Gα(θα)=G(α,θα)=G(θ,α,θα)⊆G(θ,α)。又因为(A,α)≤(H,θ)≤G且(A,α)∈IS(G),所以由惯性群引理3,易知G(θ,α)⊆G(θα)，迫使G(θ,α)=G(θα).

(3)⟹(4)因为(Hα,θα)∈IS(Gα)，且(A,α)∈IS(G),所以

Ind:Irr(Gα(θα)|θα)→Irr(Gα|θα)和Ind:Irr(Gα|α)→Irr(G|α).

均为双射。进而Ind:Irr(Gα(θα)|θα)→Irr(G|θα)也是双射。又Gα(θα)≤G(θα),由诱导源基本性质可知Gα(θα)=G(θα)从而(Hα,θα)∈IS(G).

(4)⟹(5)因为(Hα,θα)∈IS(G),所以Ind:Irr(G(θα)|θα)→Irr(G|θα)是双射。又G(θα)=G(θ,α),从而Ind:Irr(G(θ,α)|θα)→Irr(G|θα)自然也是双射。

Ind:Irr(G(θ,α)|θ)→Irr(Gα|θ)

2 复合Clifford对应

为证本文定理B,我们需要引用特征标理论中的几个经典结果。首先给出特征标的一个限制对应,其证明可见[21]中的引理10或[22]中的引理2.11。

按照[21]中的术语,我们称(G,K,L,θ,φ)为一个特征标五元组,如果L≤K均为群G的正规子群,使得K/L为交换群,θ∈Irr(K)和φ∈Irr(L)都是G-不变的,并且φ和θ关于K/L相互完全分歧,即θL=eφ和φK=eθ,其中e为正整数。称子群H为该五元组的一个补,如果HK=G且H∩K=L.

在奇数条件下,即|K:L|或|G:K|为奇数时,Isaacs构造了G的一个典范特征标,并据此建立了著名的完全分歧对应定理,即[21]中定理9.1,但本文无需使用如此强的结果。事实上,在定理B的证明中,我们需要的仅仅是该定理的一个下述推论,其证明亦可见Isaacs的最新特征标教材[22]中定理7.5。

引理5设(G,K,L,θ,φ)为一个特征标五元组,如果|K:L|>1为奇数,则存在某个子群H≤G,使得HK=G和H∩K=L,并且对每个ξ∈Irr(H|φ),均有ξG为可约的特征标。

我们还需要一个技术性概念。根据Lewis在[23]中引入的术语,如果L≤K均为群G的正规子群,则称(G,K,L)为一个正规三元组。如果还存在G的一个正规子群M≥K,满足条件(|M:K|,|K:L|)=1,并且CK/L(H)=1,其中H/L为K/L在M/L中共轭唯一的补,则称正规三元组(G,K,L)是可控的。

以下是可控正规三元组的一个基本性质,其证明属于初等群论,方便起见,我们给出证明概要。

引理6 设(G,K,L)为一个可控的正规三元组,则存在共轭唯一的子群U满足UK=G且U∩K=L.

有了上述预备,我们现在可以证明本文的第二个主要结果,即引言中提及的定理B。

定理2 设T=(G,N,ψ)为特征标三元组,如果N为可解群且ψ(1)为奇数,则ISC(T)=CCC(T).

证明我们先证CCC(T)⊆ISC(T)。任取T′=(G′,N′,ψ′)∈CCC(T),由定义,存在一个子特征标三元组的序列T=T0,T1,…,Tn=T′,使得Ti≤cTi+1,或Ti+1≤cTi,其中i=0,…,n-1。我们对n做归纳法。当n=0时,则T′=T0=T,显然是自身的诱导源对应,即T′∈ISC(T),结论成立。根据归纳假设,则T1,T2,…,Tn-1∈ISC(T),我们只需证Tn=T′∈ISC(T)。令Ti=(Gi,Ni,ψi),对任意1≤i≤n-1，因为Ti∈ISC(T)，所以(ψi)N=ψ，当Tn≤cTn-1时,则ψn=ψ′，而(ψn)Nn-1=ψn-1，故(ψ′)N=(ψn)N=((ψn)Nn-1)N=(ψn-1)N=ψ，即证T′∈ISC(T)。当Tn-1≤cTn时，则ψn=ψ′，此时(ψn-1)Nn=ψn=ψ′，故

(ψn-1)N=((ψn-1)Nn)N=(ψn)N=(ψ′)N=ψ,

亦有T′∈ISC(T)。至此即证CCC(T)⊆ISC(T).

以下证明反包含关系ISC(T)⊆CCC(T)。使用反证法,假设所证包含关系不成立,在所有的反例T′=(H,M,φ)∈ISC(T)-CCC(T)中,我们依次选取|G|和|G:H|尽可能地小。我们将逐一验证下述结论,最终导出一个矛盾,从而完成本定理的证明。

(1)H为G的极大子群。

如果H=G,则M=N∩H=N,即T′=T∈CCC(T),与T′的选取矛盾,故H

(2)令L=CoreG(M),则ψL存在唯一的不可约分量α,从而α∈Irr(L)为G-不变的。

任取α∈Irr(L)使得(L,α)≤(M,φ)≤(N,ψ),因为L◁G,故可使用(L,α)做T的Clifford约化得到Tα=(Gα,Nα,ψα)。同理,亦可使用(L,α)做T′的Clifford约化得到Tα′=(Hα,Mα,φα)。已知T′为T的诱导源对应,即(M,φ)为G的一个诱导源,根据定理,则(Mα,φα)也是Gα的诱导源,故可做Tα的诱导源对应得到特征标三元组(Gα(φα),Nα(φα),ψα(φα)),其中ψα(φα)为ψα的诱导源对应。又因为Gα(φα)=G(α,φ)=G(φα)=Hα,所以ψα(φα)=φα且Nα(φα)=Mα,由此表明Tα′为(Mα,φα)对Tα所做的诱导源约化,即Tα′∈ISC(Tα)。如果Gα

(3)任取K/L为G的一个主因子且K≤N,则(N,K,L)为可控的正规三元组。

因为L≤M

进而,从T′不是T的复合Clifford对应,可知M不能是N的正规子群,故L

(4)应用Isaacs的完全分歧对应定理导出最后的矛盾。

我们在上述已证α∈Irr(L)为G-不变的,并且K/L为G的主因子,应用特征标的上升定理,则α或者可扩张到K上,或者在K上完全分歧。如果α可扩张到K上,因为K/L为交换群,根据Gallagher对应(见[20]中推论6.17),熟知线性特征标群Lin(K/L)可传递置换集合Irr(K|α)。但S/K可共轭作用该集合上,两个群作用显然是相容的,并且这两个群具有互素的阶,根据Glauberman不动点引理(见[19]中引理13.8),则S/K在Irr(K|α)上的共轭作用具有唯一的不动点,即α在K上存在唯一S-不变的扩张β。对任意g∈G,因为g固定L,K,S,α均不变,故βg也是α在K上S-不变的扩张,再从唯一性推出βg=β,表明β也是G-不变的。特别地,此时ψ必然在β上方,故可在下面图2中使用特征标的限制对应即引理4,则ψ∈Irr(N|β)在M上的限制ψM=φ不可约,与φN=ψ矛盾,由此表明α不能扩张到K上。